数値計算〜微分方程式を解く

表計算ソフトウエアを数値計算のために利用することができる。ここでは、繰り返し代入操作を行うことによって微分方程式を数値的に解いてみる。

変数

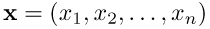とその関数

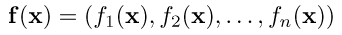に関する微分方程式

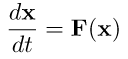
において、時刻 to での初期値 X(to)から定まる真の解 x(t)を求める代わりに、十分に小さな差分刻みΔtによって

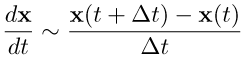と微分項を置き換えて、元の微分方程式を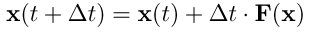

と近似して、初期値 x(to) から to+Δt での値 x(to+Δt)を、さらに値 x(to+Δt) から時刻 to+2Δt での値 x(to+2Δt) というように微分方程式の解を逐次的に求める方法が考えられる。この差分近似による微分方程式の数値解法をEuler法という。

ベクトル表記を使わずに直接的に記述するなら、微分方程式の組

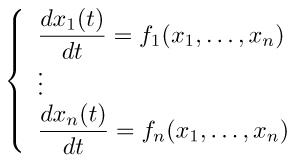
を差分方程式の組

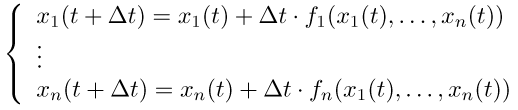
で近似して、初期値から時間刻みΔtごとに逐次数値解を求めていくのである。

ここで利用する微分方程式：
指数的に減衰する微分方程式
調査振動子（バネの振動）
Lorenz方程式

注意: Webブラウザ内で開かないで、一旦ダウンロードしてファイルとして保存してから、そのファイルをOpenしてください。

課題

与えられた微分方程式をEuler差分法で数値的に解き、その様子をグラフ化しなさい。
差分刻みΔtを様々に変えて、数値解の様子を観察しなさい。

研究

微分方程式の計算誤差を少なくするためにさまざまな差分方法が研究されている。それらを調べてみなさい。