杉原 厚吉

第18回錯覚ワークショップ

錯視作品展示スケジュール

• 2024年7月13日（土）〜2024年9月1日（日） 「どげんなっちょっと？展」 、 鹿児島県民交流センター（鹿児島市）約100点（錯視絵23点、小型立体63点、大型立体10点など）
• 2024年7月19日（金）〜2024年9月1日（日） 「大錯覚展」 、 壱岐市立一支国博物館（長崎県壱岐の島）約50点
• 2024年8月2日（金），3日（土）　明治大学中野キャンパス オープンキャンパス現象数理学コーナー　錯視立体新作約10点（二科美術展彫刻部入選作など）
• 2024年10月12日（土）〜2024年12月1日（日）　千葉県立現代産業科学館　（市川市）立体作品22点（等身大作品1点を含む）

２０２０年ベスト錯覚コンテスト優勝 「立体版シュレーダー階段図形」

　

• 立体版シュレーダー階段図形が、２０２０年の ベスト錯覚コンテスト（Best Illusion of the Year Contest 2020）で 優勝（First Prize）を獲得しました。 この立体は、紙工作で簡単に作れます。詳しくは、 ここ をご覧ください。
• 岐阜県の飛騨山王宮日枝神社へ、変身タイリングで作った 変身さい銭箱 が奉納されました。 こちら をご覧ください。
  
• 三方向多義立体が、２０１８年の ベスト錯覚コンテスト（Best Illusion of the Year Contest 2018）で 優勝（First Prize）を獲得しました。 三方向義立体についてはこちらをご覧ください。
• 日本図学会主催の第10回デジタルモデリングコンテスト（2018年）で、第8世代の鏡映合成変身立体作品「鏡に浮かぶトランプマークと花」が 最優秀賞をいただきました。 　詳しくは こちらをご覧ください。
• 岡山県の石上布都魂神社へ、錯覚作品で作った 変身さい銭箱 が奉納されました。 こちら をご覧ください。
  
• 台湾の 故宮博物院で不可能立体が展示されています。 2018年9月21日から2020年5月24日まで。 こちら をご覧ください。
  
• ミネソタ大学数学応用研究所(IMA)で行った市民講演 IMA Publid Lecture のビデオが公開されました。 こちらをご覧ください。
  
• CNNのウエブページ CNN Style で錯視立体が紹介されました。 こちら をご覧ください。
  
• BBCのウエブページ BBCワールド（スペイン語版）で、錯視立体が紹介されました。 こちらをご覧ください。
  
• 変身立体が ジュエリーになりました。 こちら をご覧ください。
  
• 次の本を出版しました。
  「鏡で不思議体験！　立体トリック工作キットブック」）、金の星社、2024年7月
  　鏡に映すと錯覚が起きる立体を台紙から工作できる新しい本です。特徴は、鏡に映すと姿勢が変わるものを集めたことです。左右が入れ替わったり、高さが入れ替わったり、正面を向いたものが振り向かなかったりです。これらの錯覚は、対称性などの立体がもつ明確な性質によって起こります。このことを理解すると、自分自身のオリジナルな錯覚作品も作れるようになるでしょう。
  
  「鏡のトリック立体キットBOOK」）、永岡書店、2021年6月
  　錯視立体の工作キットを新しく出版することができました。「吊り橋とアーチ橋」など、鏡に映すと姿が変わる立体4種類が含まれています。また、ある方向から見ると立方体に見えるのに、実は4種類の異なる立体であるという奥行き錯視の基本がわかる立体例も含まれています。
  
  「錯覚！立体ペーパークラフト」、あかね書房、2020年9月。 こちら をご覧ください。
  
  「錯覚クイズ」、だいわ文庫、大和書房、2018年4月。 こちら をご覧ください。
  
  「新錯視図鑑」、誠文堂新光社、2018年7月。 こちら をご覧ください。
  
  
• 変身立体の プラスチックモデル４種類が、次のセットで発売されています。
  「鏡で変身！？ふしぎ立体セット」、東京書籍、2017年7月。 こちら をご覧ください。
  
  

進化する不可能立体

• だまし絵立体（１９８０〜）
  　不可能立体の絵と呼ばれるだまし絵があります。これは、普通は絵には描けるけれど立体としては作れないと思われていました。でも、不可能立体の絵の中には、その名に反して、立体として作れるものもあります。それが「だまし絵立体」です。
  
  
• 不可能モーション立体（１９９０年代〜）
  　立体自体は、ありふれた形に見えるのに、そこに動きを加えると，あり得ないことが起こっているという印象を作り出すことができます。そのような動きを作り出す立体が、「不可能モーション立体」です。
  
  
• 変身立体（２０１４〜）
  　鏡に映すと形がまったく変わって見える立体を見つけました。まるで、変身するみたいに見えます。
  
  
• 透身立体（２０１５〜）
  　鏡に映すと、一部分が消えたり、無かった部分が現れたりする立体を見つけました。透明人間のように，体の一部が透けてしまうのです。
  
  
• トポロジー攪乱立体（２０１６〜）
  　鏡に映したとき、立体の形は変わらないのに、トポロジー（繋がり方）が変わってしまいます。離れた2個の円柱が、鏡の中で交差した2個の円柱に変わるなどです。
  
  
• 軟体立体（２０１６〜）
  　立体を回転させると、形が連続に変形していくように見える立体です。右を向いている矢印を１８０度回転させて左へ向けようとしても、徐々に形が変わっていってまた右を向いてしまうなどです。
  
  
• 高さ反転立体（２０１７〜）
  　立体を鏡に映すと、高さが反転してしまう立体です。その結果、全く別の立体に見えてしまいます。
  
  
• 鏡映合成変身立体（２０１７〜）
  　立体自体は意味不明の形をしているのに、水平な鏡の上に置くと、意味のある形が見えてきます。もとの立体と鏡に映った像とを合成すると意味のある形が作られるわけです。しかも、その図形は、上下対称ではありません。
  
  
• 三方向変身立体（２０１８〜）
  　３つの方向から見たとき、３種類の異なる姿が見えてきます。
  
  
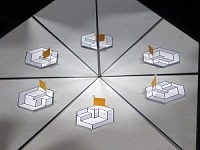• 六方向変身立体（２０１８〜）
  　６つの方向から見たとき、６種類の異なる姿が見えてきます。
  
  
• 変身タイリング（２０２０〜）
  　1種類のタイルで、隙間も重なりもなく平面を埋め尽くすタイリングパターンが、鏡の中で別のタイリングパターンへ変身します。
  
  
• 穴変身立体（２０２０〜）
  　立体の代わりに、立体にあけた穴が鏡の中で変身します。
  
  
• 起き上がり立体（２０２１〜）
  　横たわった立体が、鏡に映すと起き上がります。
  
  
• 回遊立体（２０２２〜）
  　複数の生き物とその鏡像が輪になって回遊します。
  
  
• 平行移動立体（２０２２〜）
  　鏡に正面を向いたものが、鏡の中で振り返らないで平行移動します。
  
  
• 回転並進混合立体（２０２３〜）
  　立体が正面の鏡の中へ平行移動する平行移動錯視と、横に立てた鏡の中で向きが反転する左右反転錯視が同時に置きます。
  
  
• 一人回遊立体（２０２３〜）
  　一つの立体を直交する二枚の鏡に映すと、立体と3つの鏡像の合計４体が輪になって回遊します。
  
  
• 半身回遊立体（２０２３〜）
  　頭部の半身または尾部の半身を鏡に付けると全身が現れ、それがもう一つの鏡の中で左右反転します。この半身立体を２個組み合わせると、向きがそろって輪になります。
  
  
• 独り回遊立体タイプ２（２０２４〜）
  　１２０度で交差する２枚の鏡の前に立体を置くと、立体とその二つの鏡像の合計３体が向きがそろって輪になります。
  
  
• 不可能立体を自由研究・文化祭などで使っていただいている皆様へ
  　たくさんの方に使っていただき、ありがとうございます。せっかくですので、不可能立体をきっかけにいろいろ考えてみてはいかがでしょう。 　
  

品切の著書の公開

• Machine Interpretation of Line Drawings (MIT Press) の全文公開

---

• ニュース・イベント情報

---

関連リンク