http://www.isc.meiji.ac.jp/~mizutani/
Lorenz系をRで数値計算
$(x,y,z)\in \mathbb{R}^3$内ベクトル場が次の非線形微分方程式系 \begin{align} \frac{dx}{dt} &=\sigma (y-x)\\ \frac{dy}{dt} &=r x -y - xz\\ \frac{dz}{dt} &=-b z + xy \end{align} で記述される系をLorenz方程式という [Deterministic Nonperiodic Flow (Edward N. Lorenz, J. Atmos. Sci., 20(11963), 130–141）]。 Lorenzにならって、$\sigma = 10$, $b=8/3$と固定し、$r$を様々に変化させるパラメータとする。
準備的考察
ベクトル場$\mathcal{X}=(v_1,\dots,v_n)$の発散（divergence）を${\rm div}\mathcal{X}\equiv \sum_{i=1}^n \displaystyle\frac{\partial v_i}{\partial x_i}$ で定める。 ベクトル場の発散は、相空間内にしめる領域$V$の時間変化を表していると考えることができる。 Lorenz方程式で定まるベクトル場の発散は \[ \frac{\partial }{\partial x}\left(\frac{dx}{dt}\right)+\frac{\partial }{\partial y}\left(\frac{dy}{dt}\right)+\frac{\partial }{\partial z}\left(\frac{dz}{dt}\right)= -(\sigma + b + 1) \] となることから、x-y-z空間内で占める初期領域の体積を$V_0$としたとき、$V(t)=V_0e^{-(\sigma + b + 1)t}$、つまり$t\rightarrow\infty$でどんな領域の体積は指数的に$0$に収縮する。
$r < 1$のときは原点$(0,0,0)$が唯一の不動点で、原点のまわりで線形化した特性方程式 \[ (\lambda + b)(\lambda^2 +(\sigma +1)\lambda +\sigma(1-r))=0 \] の根を調べると、$0 < r <1$ のときには3実根は全て負となっていて原点は漸近安定点であることがわかる。 $1 < r$ のとき、1つの実固有値が正となって、原点は1次元不安定多様体と2次元の安定多様体が交差する双曲不動点となる。 この$1 < r$のときには、新しく2つの不動点 $C_{\pm}$ \[ C_{\pm}=(\pm\sqrt{b(r-1)}, \pm\sqrt{b(r-1)}, r-1) \] が現れることに注意する（z成分は2点とも$r - 1$で、同じ高さにある）。
2つの不動点 $C_{\pm}$のまわりで線形化したときの特性方程式 \[ \lambda^3 (1+b+\sigma)\lambda^2 + b(r+\sigma)\lambda + 2b\sigma(r-1)=0 \] の根を調べてみる。 $1 < r < r_s=1.34561\dots$ のときは3つの負の実根となり、$C_{\pm}$は安定結節点である。 $r_s < r < r_c=\sigma \displaystyle\frac{\sigma+b+3}{\sigma - b -1}=24.768\dots$ で、1つの負の実根と1組の負の実部を持つ複素共役根を持ち、$C_{\pm}$は安定点である。 $r_c\leqq r$ で $C_{\pm}$は不安定化することが分かる。
ストレンジアトラクター
詳しい解析によると、$r_c\leqq r \leqq 30.1\dots$ では、$C_{\pm}$を通過する1次元安定多様体が存在し、$\mathbb{R}^3$全体ではストレンジアトラクター(strange attractor)と呼ばれる、薄く平面的に見えながらも複雑な構造を持つ大域的アトラクターが存在することが分かっている。 「ストレンジ」というのは、このアトラクターが点でも線や$S^1$のような1次元的でもないが1次元方向とは垂直な方向に薄いCantor集合的な構造を持っているために考案された造語である。
ストレンジアトラクターが存在するとき、$\mathbb{R}^3$内のどんな初期条件から出発した軌道も、このストレンジアトラクターに引き込まれ、その挙動はLorenzの論文で初めて指摘されたように非周期的である（周期的でないのであるから、非周期的軌道は1本の無限の長さの紐であるとイメージしてほしい）。 以下、この$r=28$のときのストレンジアトラクターの様子を調べてみよう。
ローレンツ系のベクトル場はsmoothであり、したがって解の存在と一意性は保証されている。 つまり、smoothなベクトル場で定義される力学系の相空間は「異なる」軌道で連続的に埋め尽くされている。 つまり、ある初期条件$(x_0,y_0,z_0)$から出発する軌道$\mathcal{O}(t,x_0,y_0,z_0)$は唯一つに定まり、$\mathcal{O}(t,x_0,y_0,z_0)$上にない異なる初期条件$(x'_0,y'_0,z'_0)$からから出発する軌道と交差することはない。
$\mathbb{R}^3$内のどんな軌道もこのストレンジアトラクターに引き込まれて非周期的な挙動を示すという主張は、以上の観点から理解される必要がある。 実際、以下の数値計算で観測されることは、異なるどんな軌道であってもこのストレンジアトラクターに引き込まれていくことである。 しかし、異なる軌道$\mathcal{O}(t,x_0,y_0,z_0)$は決して交差することないのであって、ストレンジアトラクターに巻き付いていく様子は各軌道ごとに異なっているのである。 そして、全ての軌道はストレンジアトラクターに引き込まれて、非周期的な運動をするというのである。 こうした状況を想像してみよう。
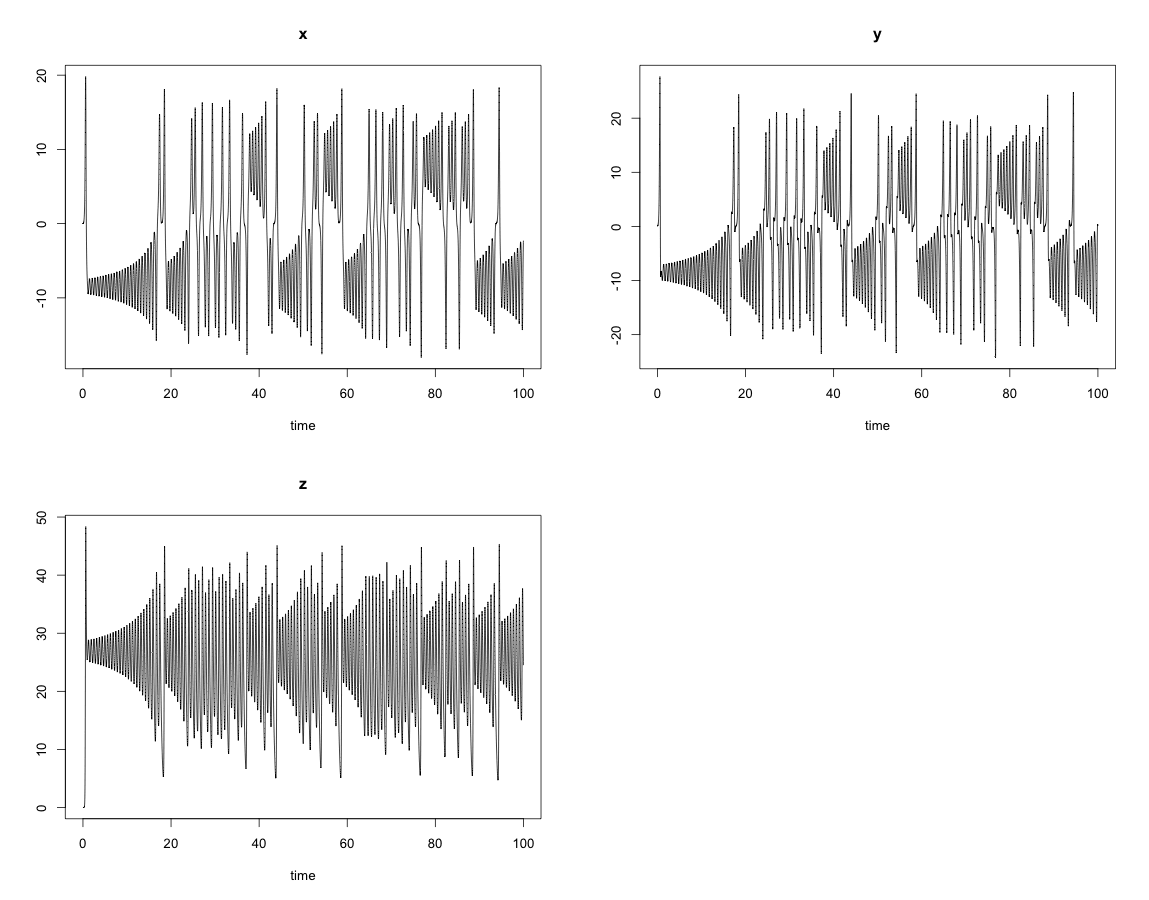左図は$r=28$としたとき、初期条件$(x_0,y_0,z_0)=(0, 0.1, 0)$で出発した際の$x,y,x$各成分の$t=0\rightarrow 100$までの変化を示したものである（差分時間刻み$\Delta t=0.01$である）。
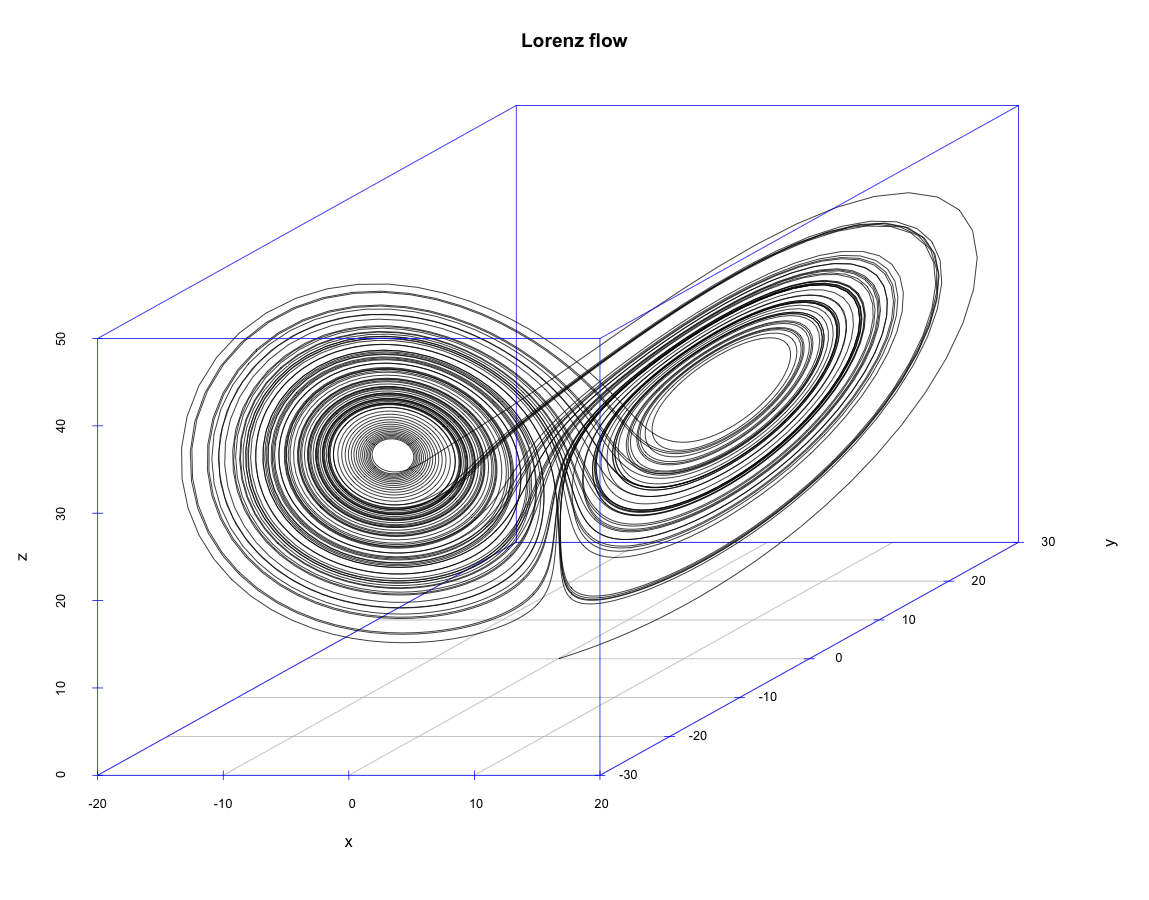左図 Lorenz flowは3次元空間内の軌道の様子である。
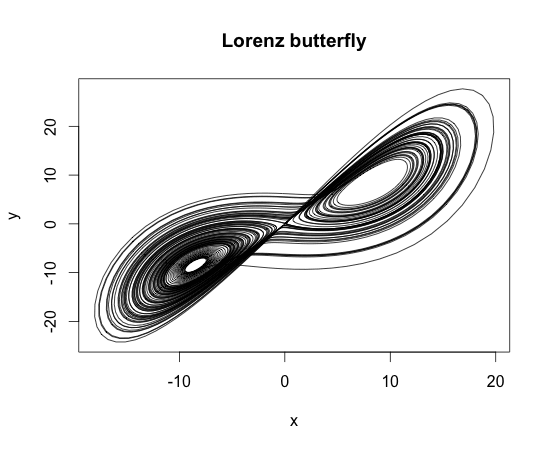右図 Lorenz butterflyは、z軸に垂直にx-y平面に射影した軌道で、蝶は羽を広げた様子に似ていることからこの名前が付いた。
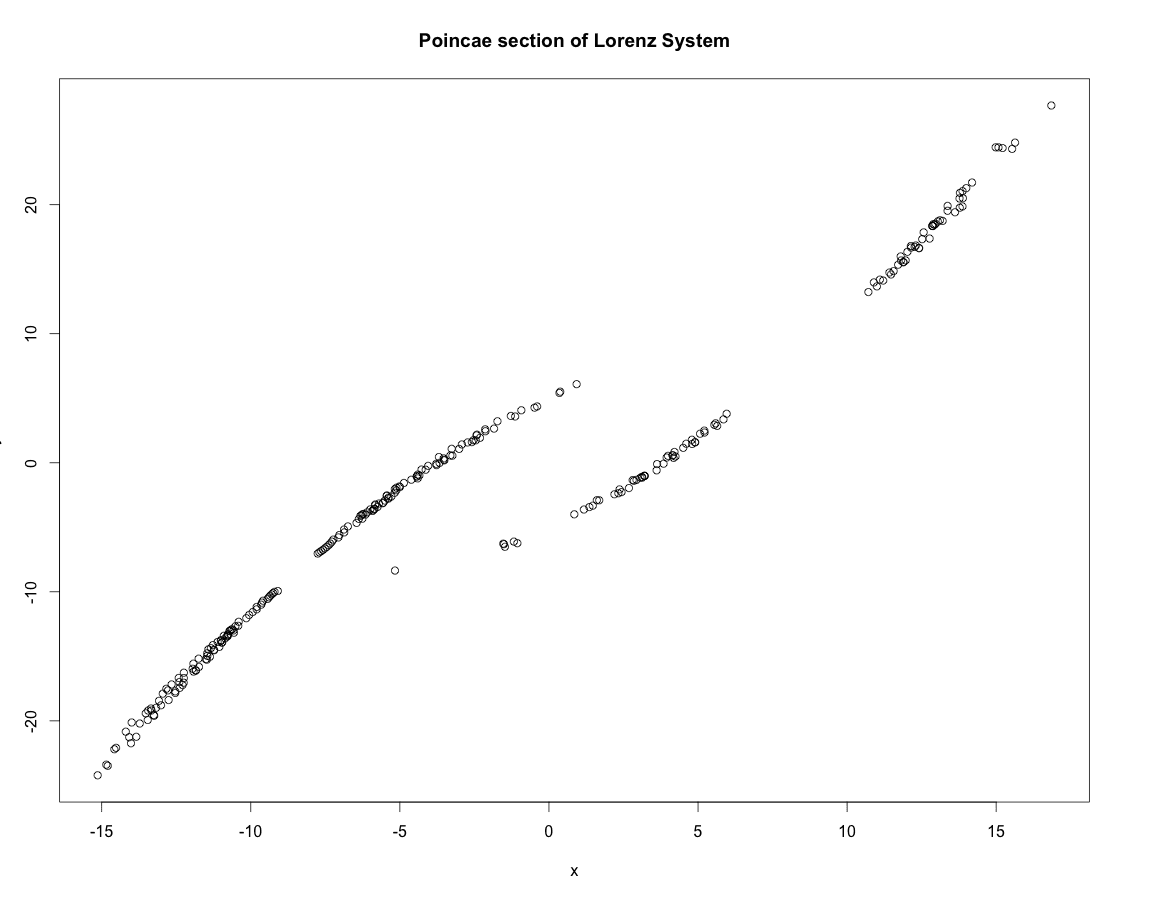右図は、x-y2次元平面$z=r-1$（2つの不動点$C_{\pm}$の高さ）を軌道が横断する点列をプロットしたPoincare surface of sectionである。
このアトラクターの断面は「1次元的」で薄いことが分かる。
2本の曲線は1次元的に見えるが、これに垂直な方向に微細なCantor集合的複雑な構造を持たざるを得ないことが分かっている。
カオス力学系
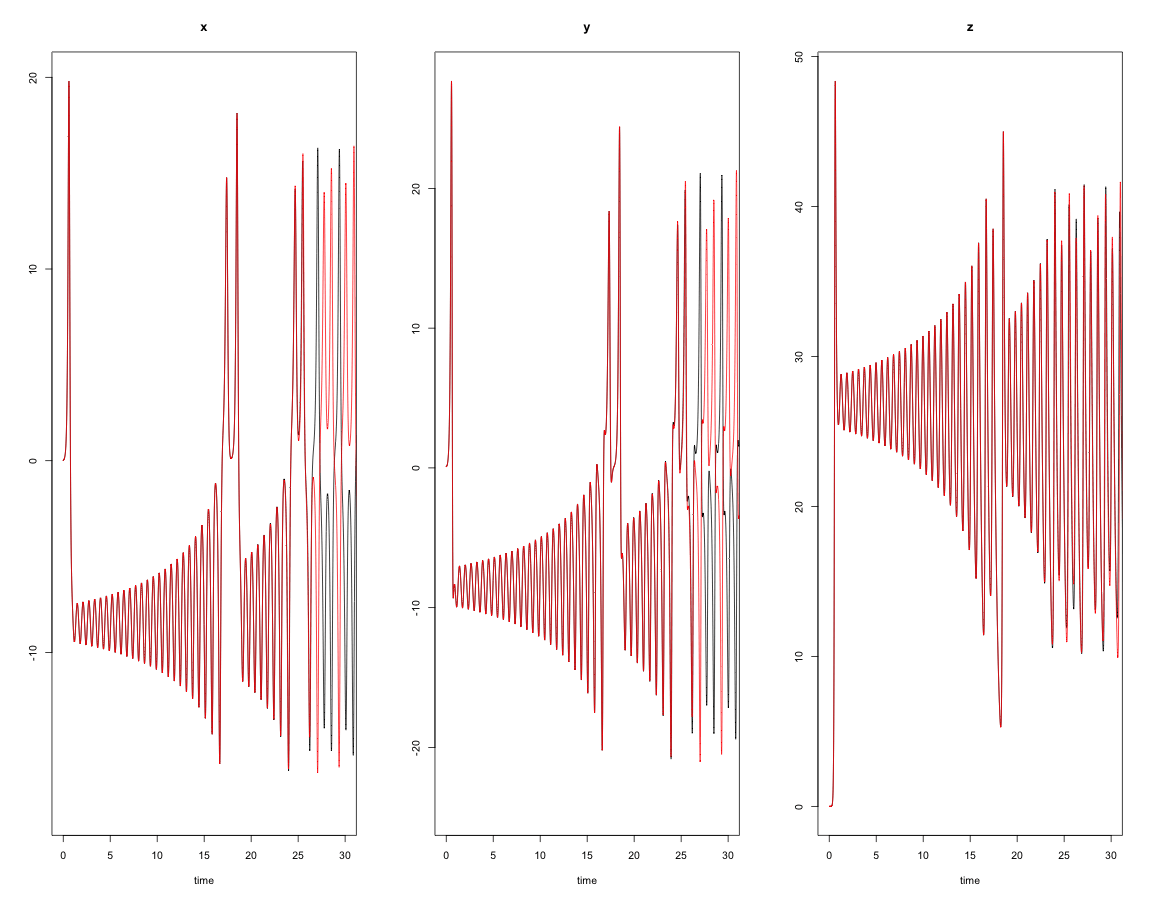僅かに異なる初期条件$(0.0001, 0.1, 0)$から出発した軌道の各成分（赤色）の時間変化の様子を時間$t=0\rightarrow 30$（$\Delta t=0.01$）まで比較したのが右図である。
$r=28$のとき、ローレンツ系は僅かな初期条件の差であっても、その後の挙動は急速に異なる相空間内の軌道となっていくことが分かる。
この性質を初期条件鋭敏性(sensitive dependence on initial condisions)という。
ローレンツ系もそうであるが、smoothな力学系では、2つの解$(x,y,z)$と$(x',y',z')$の時刻$t$での差が$\varepsilon$以下 \[ || (x(t),y(t),z(t))-(x'(t),y'(t),z'(t)) ||<\varepsilon \] となるように、時刻$t=0$ので初期条件の差$||(x_0,y_0,z_0)-(x'_0,y'_0,z'_0)||<\delta$を定めることができる。 初期条件の差$\delta$をいくらでも近くしておけば、任意の時間$t$の経過後の差を$\varepsilon$以下にできるのであるが、 初期条件鋭敏性とは、初期条件の差を$\delta$としたときにその後の軌道の差異が急速に拡大して、結果的に相空間内の軌道が大きく異なってしまう状況を表現する概念であることに注意しよう。
初期条件の差$\delta$が測定機器の計測限界以下であったとしよう。 初期条件鋭敏性を有する力学系では「同じ」初期条件を設定して状態変化を何回も繰り返した場合、その後の状態は実験するたびにその結果は異なることにる。 この意味することは非常に意味深いことであることを理解しておかねばならない。 同じ初期状態かから出発した状態変化は、実験を繰り返す度に違う結果をもたらすというのである。あたかもサイコロを振って結果が毎回異なるランダムな現象のように観察されるのである。 数学的に初期条件を与えればその後の挙動は一意的に定まる決定論的な系であるにも関わらず、あたかもランダムに振る舞う系と映るのである。 決定論的に挙動が定まっているにも関わらず、初期条件鋭敏性を有するために、あたかもランダムに振る舞い予測不可能な（あるいは確率的にしか予測できない）システム振る舞う現象をカオス（chaos）という。
では、Lorenz系は本当にカオス力学系なのであるのか？ Lorenzは、数値的な手法ではあったが、Lorenz系がカオス力学系であることを示したという先駆的研究を行った。
与えられた微分方程式系がカオス力学系であるかどうかを数学的に証明（判定）することは今日でも大きな未解決問題である。Lorenzの発見した手法は，今日ではLorenz plotと呼ばれる手法である。 この手法は非自明な力学系の簡略化（次元低減）の1つである。
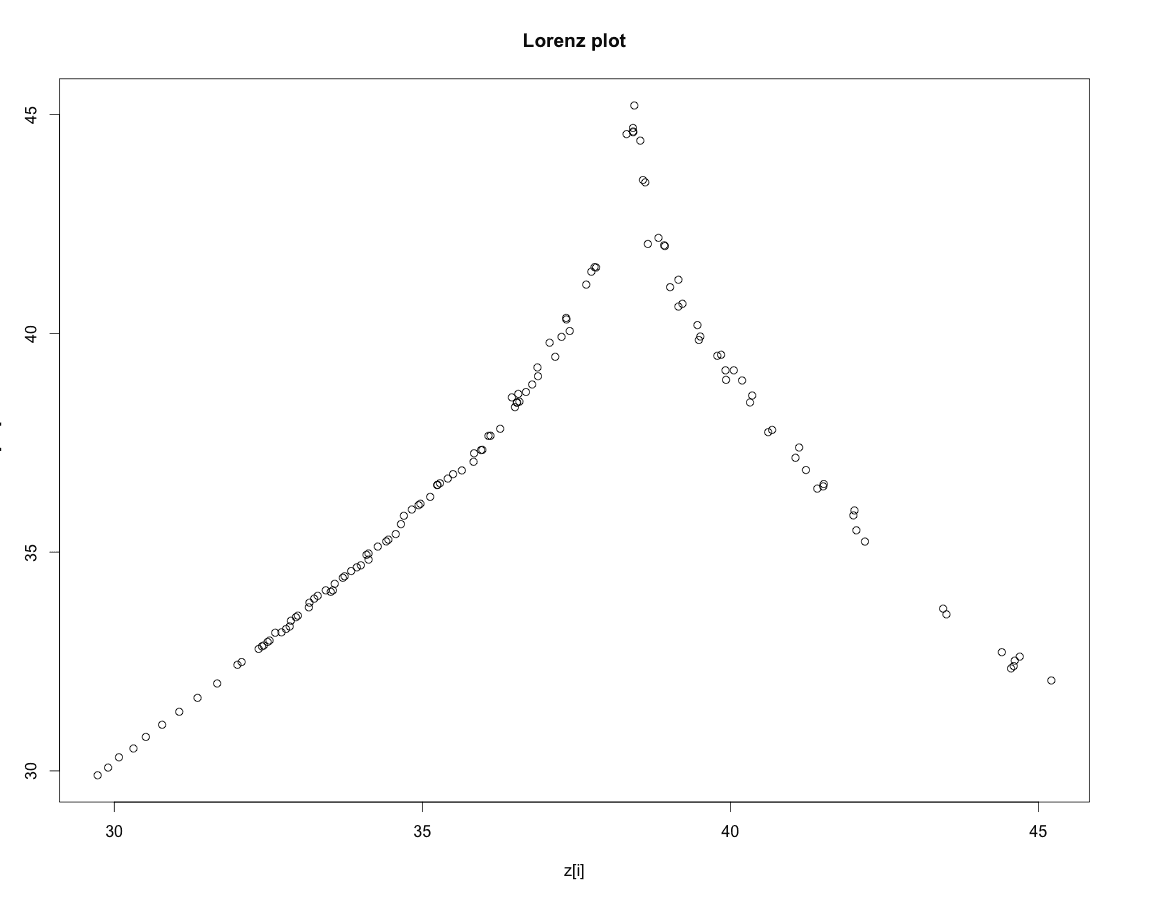
Lorenzはx,y,z成分の時間変化においてz成分だけに注目し、その相対的極大値(relative maxmimum)の無限列 \[ (z_1,z_2,z_3,\ldots ) \] を求めた。具体的には、時間刻み$\Delta t$で数値計算で求めた離散値$\{z[n\Delta t]\}_{n=0}^\infty$において、$z[(i-1)\Delta t] < z[i\Delta t] < z[(i+1)\Delta t]$ となる$z[i\Delta t]$が相対的極大値$z_i$である。 こうして数値的に求めた数値列$(z_1,z_2,z_3,\ldots )$に対して$\{(z_i, z_{i+1})\}_{i=1}^\infty$をプロットした得た左図がLorenz Plotである。
上図は、$\mathbb{R}^1$の区間$I$上の写像（関数） $L_p$ \[ \begin{array}{ccc} L_p: & z \longmapsto & L_p(z) \end{array} \] が存在して（$L_p$の傾き$\left|\displaystyle\frac{d L_p}{dz}\right|>1$であることに注意しよう）、適当な初期条件$z_1\in I$に対して写像を繰り返し適用して(iteration of map)得られる数列$\{L_p^n(z)\}_{n=0}^\infty$が相対的極大値列$(z_1,z_2,z_3,\ldots )$となることを強く示唆している。
