Meiji Mizutani Masahiro（水谷 正大） http://www.isc.meiji.ac.jp/~mizutani/

Rで表計算

Rで微分方程式

Hénon写像

M. Hénonは Lorenzの研究に刺激を受け（そのPoincare surface sectionは平面である）A two-dimensional mapping with a strange attractor (Communications in Mathematical Physics 50 (1): 69–77(1976))において、2次元平面上の写像 \[ T:\left\{ \begin{array}{ll} x_{i+1} &= y_i + 1 - ax_i^2\\ y_{i+1} &= bx_i \end{array}\right. \] を考え、これを反復して得られる点列軌道 $\mathcal{O}(T; (x_0,y_0))=\{(x_0,y_0), (x_1,y_1), (x_2,y_2), \ldots\}$ を研究した。 この研究手法は、M. Henon, M. & C. Heilesによる1964年の研究The applicability of the third integral of motion: Some numerical experiments以前になされた(p76ページ図8)、運動方程式を数値積分せずハミルトン力学系が有する基本的性質を満たす2次元面積保存写像の反復研究に基づいている（この由緒ある力学問題はあとで研究しよう）。

ただし、M. HénonはLorenz系（Roessler系）が有するストレンジアトラクターを有する解軌道の性質の本質を以下のような折れたたみ＋つぶし効果と捉えて上記の簡単な写像を導いた点が偉大である。

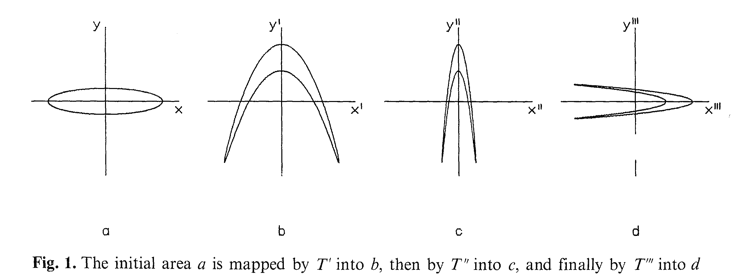右図Fig.1（論文から直接転載）のように、

  1. 軸にそった細長い領域(a)を放物的に（2次関数で）折り曲げる写像 \[ T': x'= x,\quad y' = y + 1 - ax^2\qquad (a>0) \] によって a$\rightarrow$bとする。
  2. これを、x軸に沿って圧縮する写像 \[ T'': x'' =bx',\quad y''=y'\qquad (|b| <1) \] によって b$\rightarrow$cとする。
  3. 向きを元のように復元する写像 \[ T''': x'''=y'',\quad y''' =xx \] によって c$\rightarrow$dとする。
  4. こられを次のように構成して写像$T$とする \[ T= T'''\circ T''\circ T': y +1 - ax^2,\quad bx\qquad (a>0,|b|<1) \]

この写像$T$のJacobianは \[ \frac{\partial (x_{i+1},y_{i+1})}{\partial(x_i,y_i)}=-b \] となって、Lorenz系の体積減少率が負（ベクトル波の発散が負 $\displaystyle {\rm div}\cdot \boldsymbol{f}=-(\sigma + b+1)$）に対応している。

Hénonにならって、以下パラメータ$a=1.4,b=0.3$と固定して計算してみよう。

平面上の任意の場所を初期条件$(x_0,y_0)$としてもアトラクターに引き込まれるわけではない。 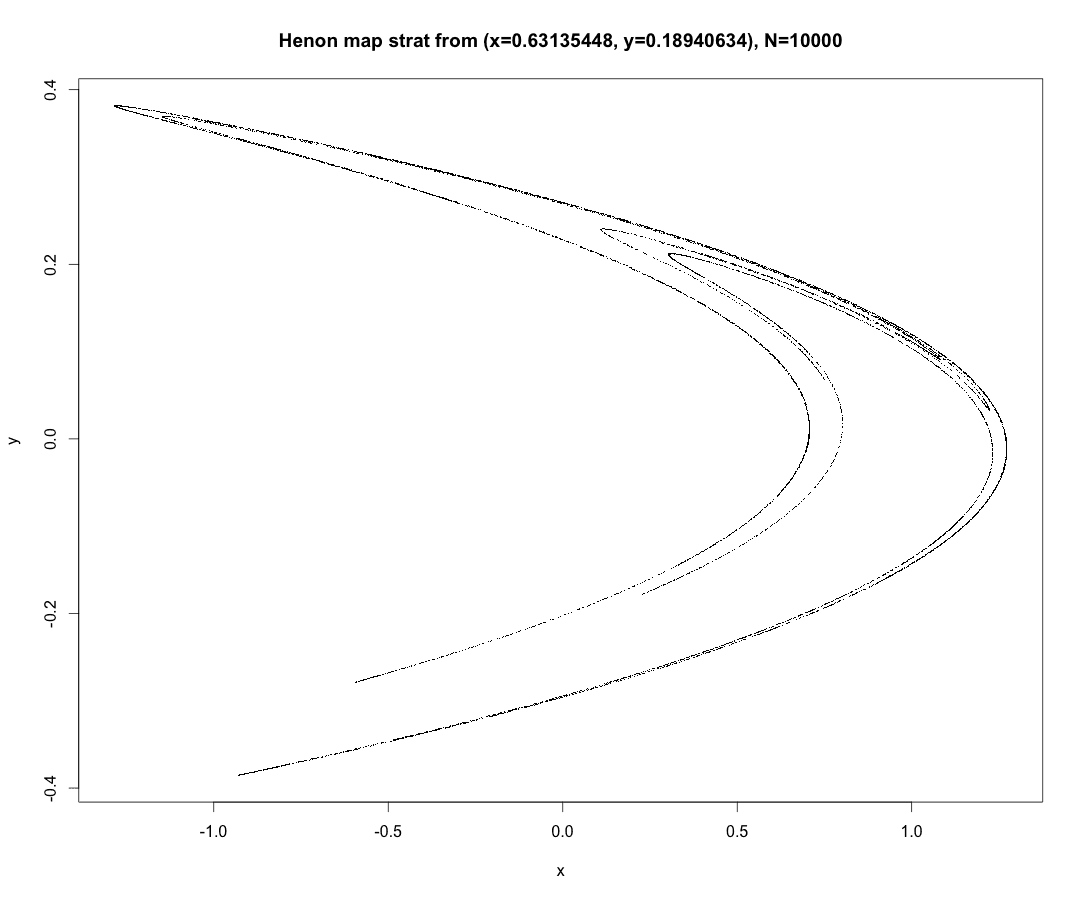座図は初期条件$(x_0,y_0)=(0,0)$として$N=10000$回反復してえた軌道の様子である（$(0,0)$と$(1,0)$に点があることに注意っしよう）。 馬蹄系のようなoretatamareta 1次元直線に軌道が載っているようにみえる。 果たしてそうだろうか？ ここではHénonの足跡をたどろう。

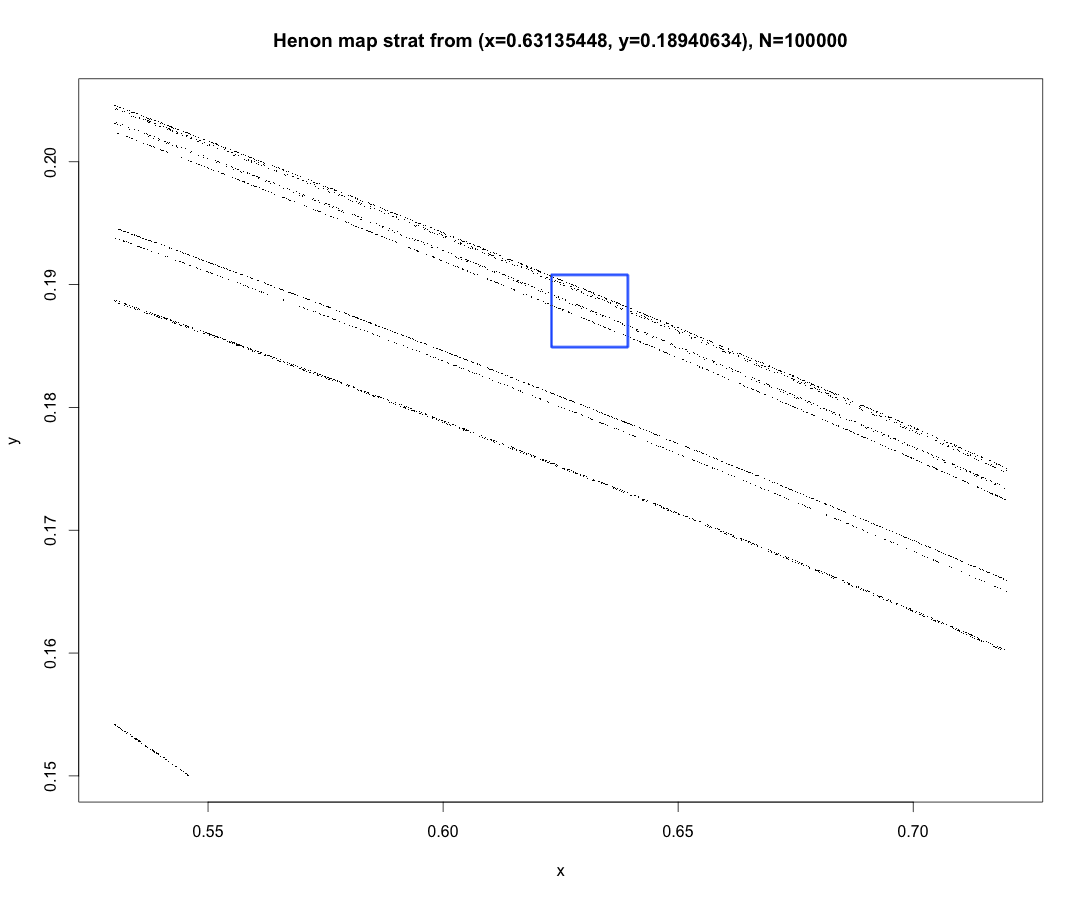
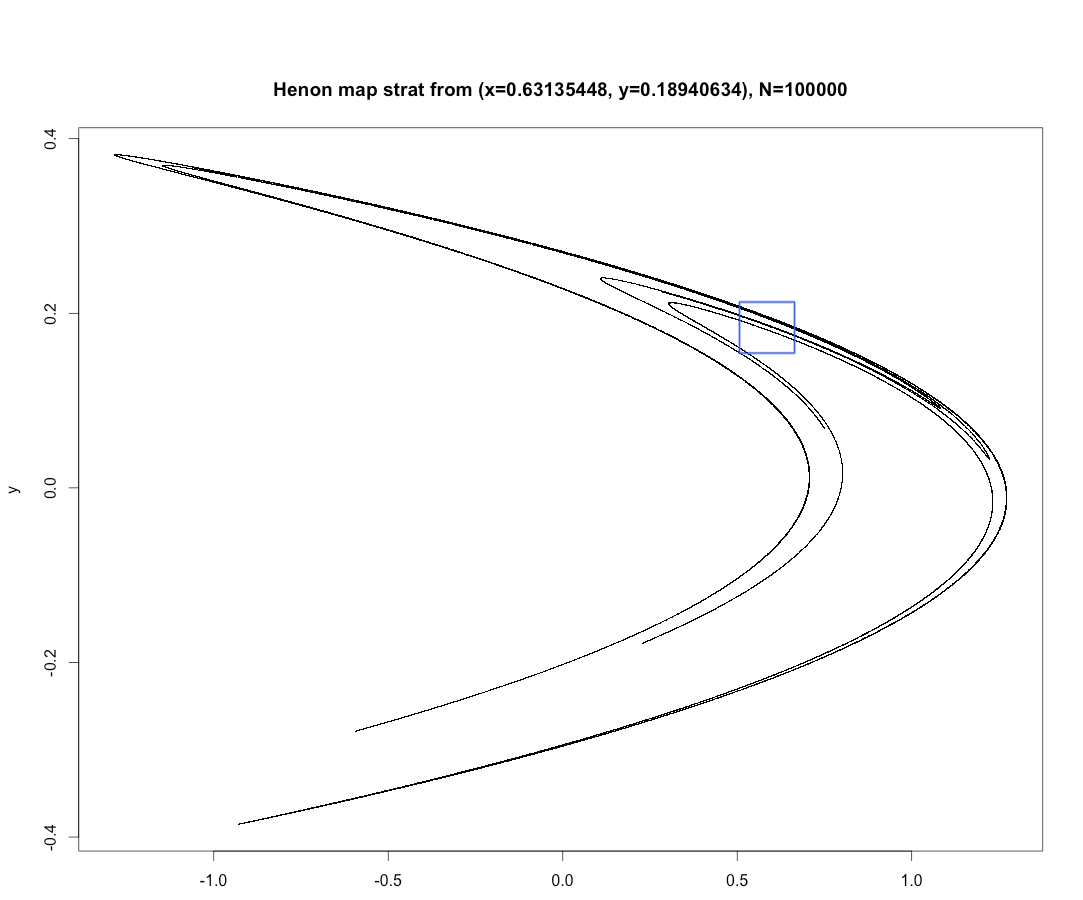Hénonは反復回数$N=10^5$に増やして、1次元的に見える部分を拡大して詳しい観察を試みた。 右図はそのアトラクターの全体図であるが、左図は右図の部分$(0.53 < x < 0.72)$および$(0.15 < y < 0.21)$を拡大して図示したものである。

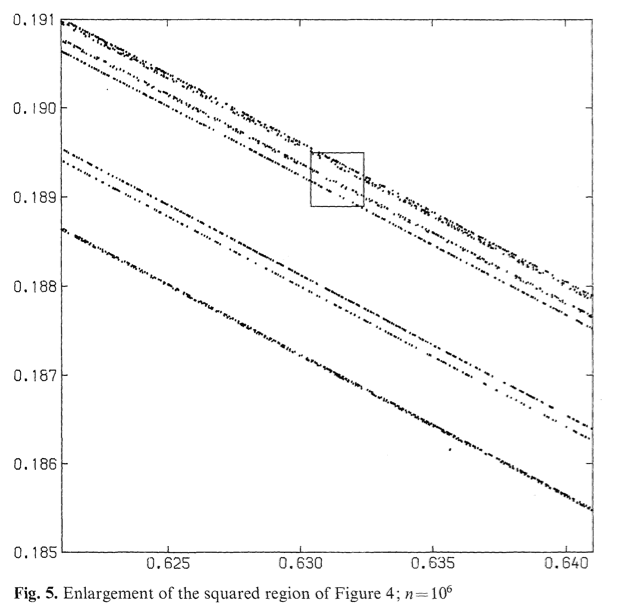
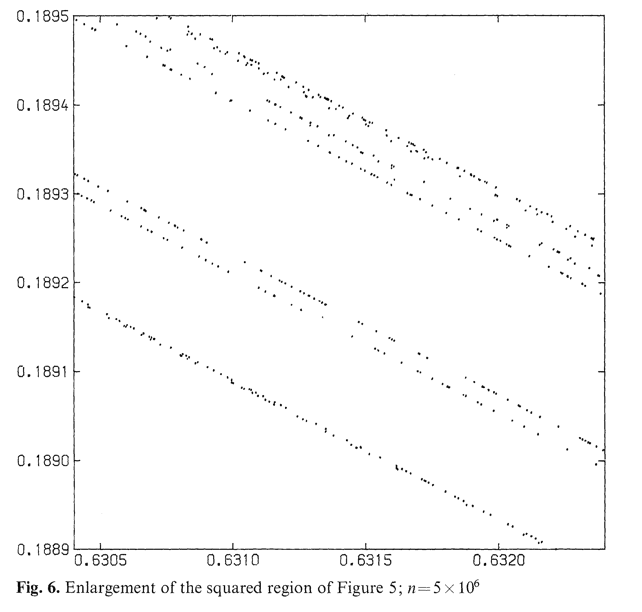さらに、Hénonは上の左図の囲んだ部分を$N=10^6$回反復して左図を、さらに$N=5\times 10^6$回反復して右図を得た


これらの結果は何を示唆しているだろうか。 Hénonは、一次元曲線的に見える軌道が成す「ストレンジアトラクター」は横断する方向にCantor集合の構造を持っていると看破したのである。
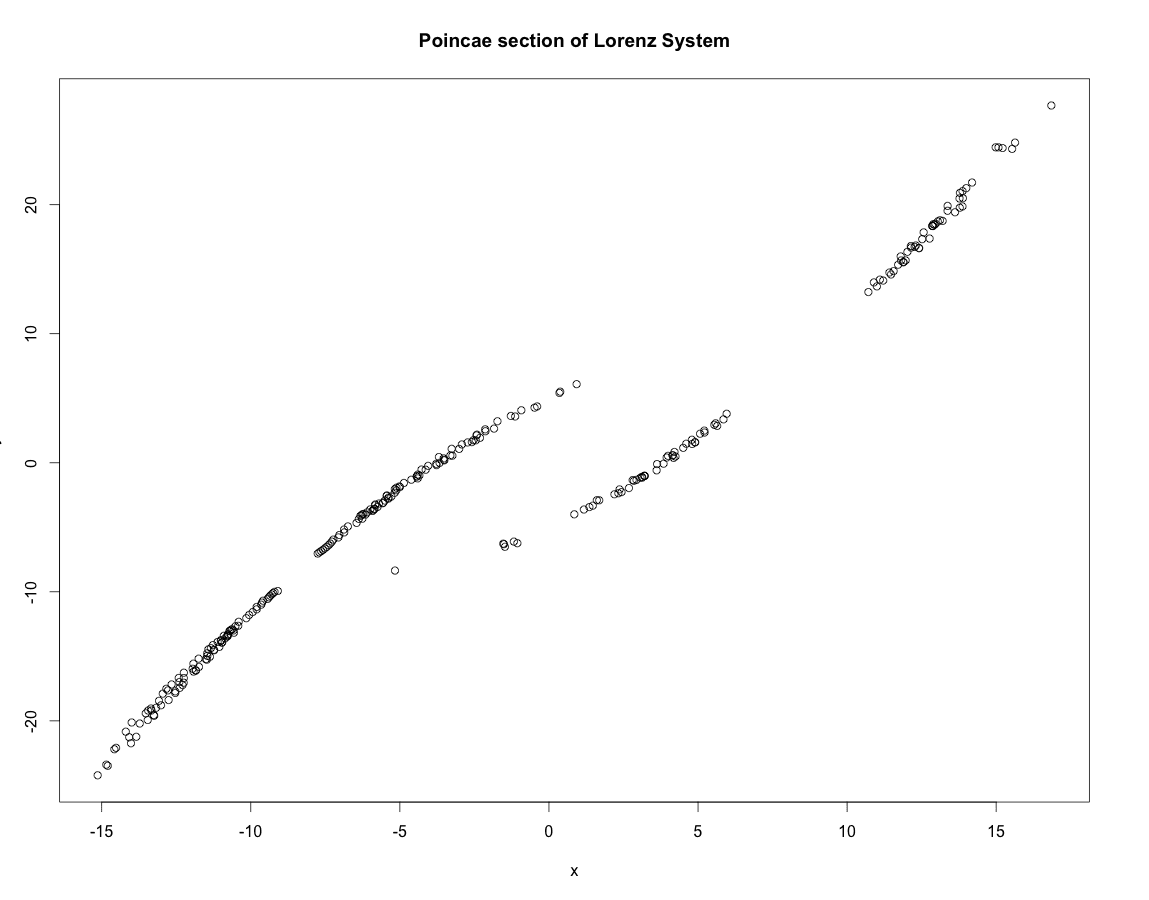
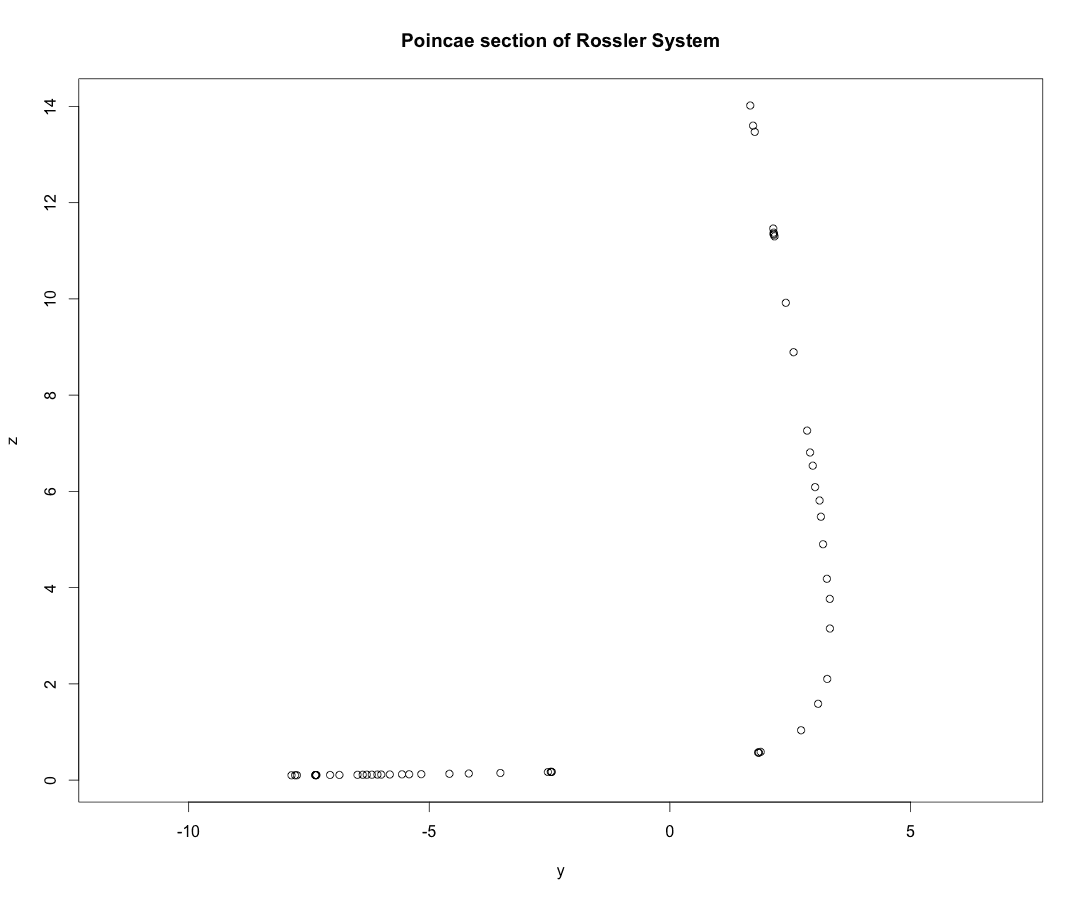非周期的なLorenz軌道やRössler軌道のPoincare surface sectionは上図のように1次元的であったことを思い出して欲しい。 Hénon写像の結果が強く示唆するように、実はこれらの1次元的な構造に横断的な方向にはCantor集合的構造が押し込まれているのだ。 不動点から伸びている安定多様体と不安定多様体が複雑に折りたたまれて、ストレンジアトラクターとなったとき、このような複雑な構造を取らざるをえないというわけである。