http://www.isc.meiji.ac.jp/~mizutani/
反復写像系（離散力学系）
あり領域$I$上の写像 $f: I\rightarrow I$ について次式\[ x_{n+1}= f(x_n), \qquad n=0,1,2,\dots \] で定義される点列 $\mathcal{O}(f; x_0)=\{x_0, x_1, x_2, x_3, \ldots\}$ を写像 $f$ の反復繰り返し(Iteration)によって生成された軌道といい、これを反復写像力学系(iterative systems) $(f, I)$ という（時間変化が写像の繰り返し回数となるという意味合いから、離散力学系(discrete systems)ともいう）。
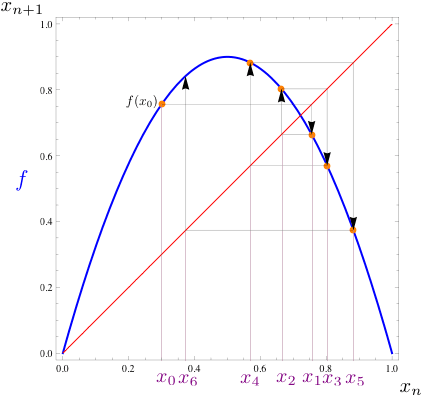つまり、初期値 $x_0$ から定まる軌道 $\mathcal{O}(f; x_0)$ は写像 $f$ のグラフを使って右図のように構成されていると理解しよう。
この例では、1次元区間$[0,1]$上の1次元写像としてMayの写像 $f_a(x) = ax(1-x), 0 < a \leqq 4$ である（$a=3.6, x_0=0.3$）。
テント写像
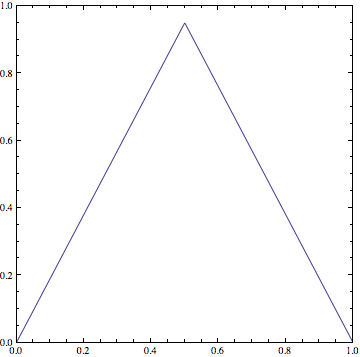
次のようなテント写像 $T_a (0 < a \leqq 2）$ \[ T_a(x) =\left\{ \begin{array}{ll} ax & \mbox{if $x\in [0,1/2)$}\\ -ax + a & \mbox{if $x\in [1/2,1]$} \end{array} \right. \] を考えよう（右図は $ a= 1.9$）。
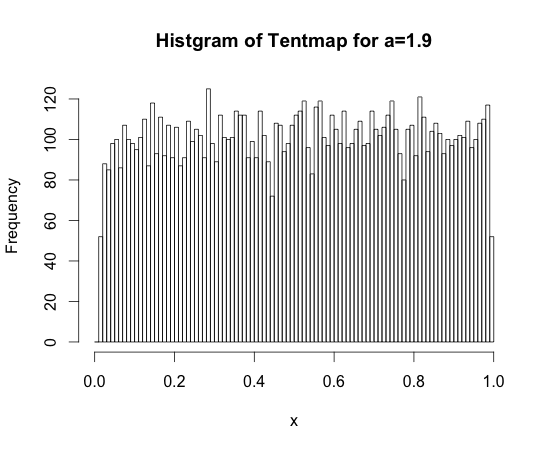左図は テント写像の傾き $a=1.99$のとき、初期値 $x_0=0.1234$ からの軌道 $\mathcal{O}(T_a; x_0)$ の最初の1万点を 区間$[0,1]$ を幅 0.01 の微少区間に100分割して、点列が各区間を訪れた頻度を描いた図である。
$a = 2$ のとき、ほとんど全ての初期値 $x_0$ について軌道 $\mathcal{O}(T_2; x_0)$ は区間 $[0,1]$ に均等に分布することが証明できる（証明を試みよ）。
$a = 2$ のとき、区間 $[0,1]$ 上にる正のLebesgue測度をサポートに持つ適当な分布 $w(x)$ （$\int_0^1 w(x)dx=1$としよう）をおいてテント写像 $T_2$ を適用することを考えてみよう。 その分布はテント写像 $T_2$ の適用によって 区間$[0,1/2)$ と $[1/2,1]$ の両方でそれぞれ横に2倍に引き延ばされて（分布の高さは半分になり）重ねられた分布となることがわかる。 このことから、Lebesgue測度正のサポートに持つどんな分布もテント写像 $T_2$ を繰り返し適用することによって、分布は区間 $[0,1]$ で高さ1の一様分布に近づいていくことがわかる。
このことは、言い換えると、僅かな誤差 $\Delta x_0$ がある2つの初期条件の$x_0$と$x_0'$ の軌道 $\mathcal{O}(T_2; x_0)$ と $\mathcal{O}(T_2; x_0')$は、テント写像 $T_2$ の反復によって \[ |T_2^n(x_0)-T_2^n(x_0')|\sim 2^n\Delta x_0 \] の程度で指数的に離れていくことも同時に示している。 つまり、テント写像力学系 $(T_{a=2}, [0,1]$ はカオス力学系である。
この考察は、1次元反復写像力学系$(f, I)$ がカオスであるかどうかの解りやすい1つの指標を示唆している。 つまり、区間 $I$ の"どこでも"その写像の傾き $\displaystyle \left|\frac{df}{dx}\right|>1$ であれば、その写像力学系はカオス的性質を示すはずである。 その根拠は、全区間で"引き延ばされ"て"重ねられる"という性質に以来している。
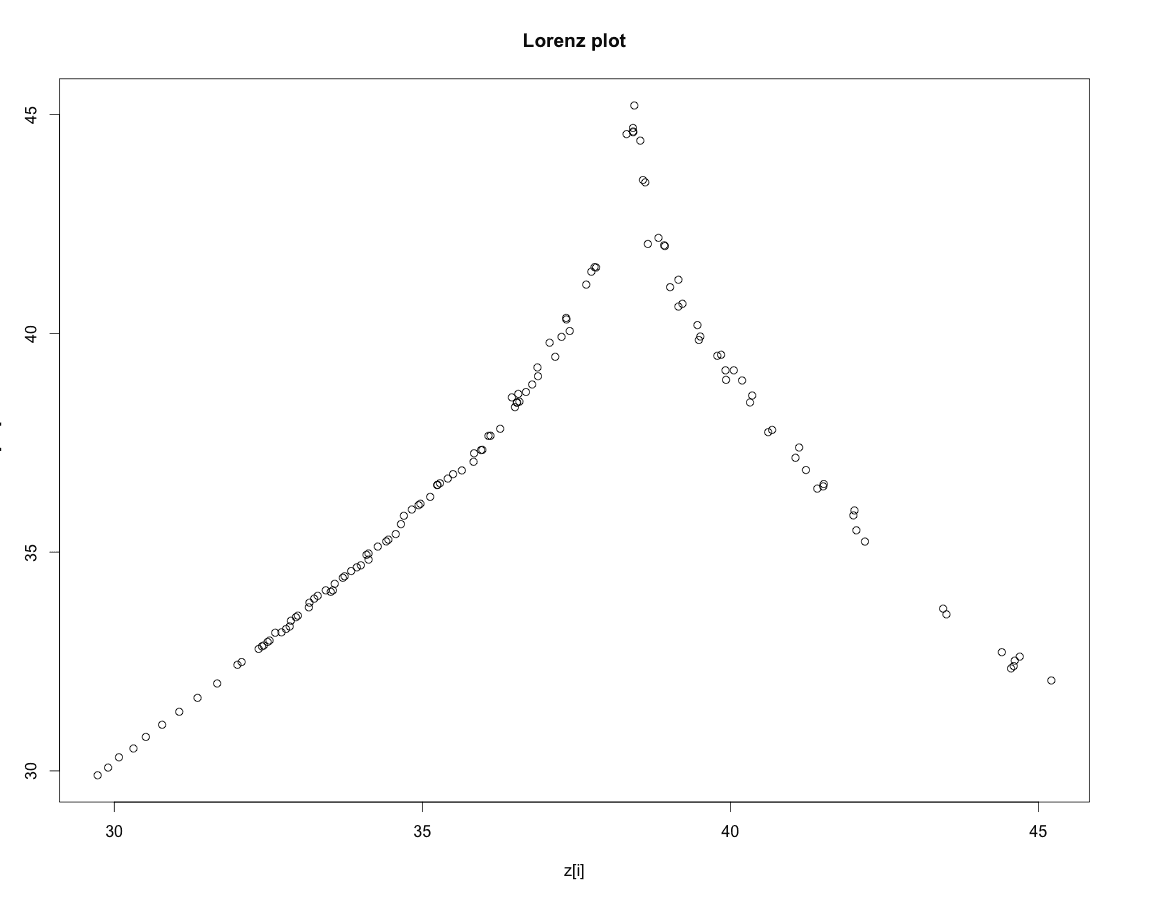
Lorenz系はカオス力学系であり得るのか？ Lorenzが発見したz成分のrelative maximum の点列のLorenz plot結果をもう一度思い起こそう。 Lorenz plotは非自明な力学系の簡略化（次元低減）の1つである。
Lorenzが得た左図は、微分方程式であるLorenz系に、1次元区間上の写像（関数） $L_p$ \[ z_{n+1}= L_p(z_n) \qquad n=0,1,2,\dots \] が存在し、その傾きは"どこでも傾き1"であるような反復力学系が埋め込まれていることを強く示唆している。
Mayの力学系
Mayの写像 $f_a(x) = ax(1-x), 0 < a \leqq 4$ の場合はどうだろうか。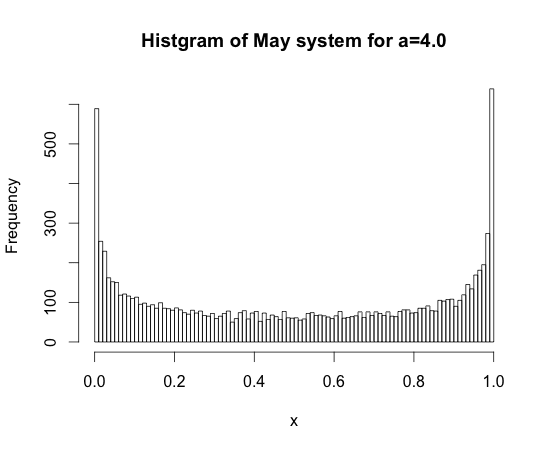
左図は $a=4$のときのMay写像の初期値 $x_0=0.3$ からの軌道 $\mathcal{O}(f_{a=4}; x_0)$ の最初の1万点を 区間$[0,1]$ を幅 0.01 の微少区間に100分割して、点列が各区間を訪れた頻度を描いた図である。 実は、$a=4$ の場合、次の分布 $m_{a=4}(x)$ \[ m_{a=4}(x)=\frac{1}{\pi}\frac{1}{\sqrt{x(1-x}}, \qquad x\in [0,1] \] は$f_{a=4}$に関して不変であることがわかる（これを不変測度(invariant measure)という）。
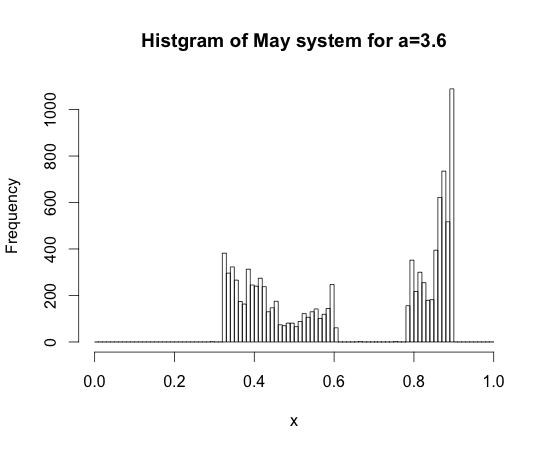一方、右図は $a=3.6$のときのMay写像の初期値 $x_0=0.3$ からの軌道 $\mathcal{O}(f_{a=3.6}; x_0)$ の最初の1万点を 区間$[0,1]$ を幅 0.01 の微少区間に100分割して、点列が各区間を訪れた頻度を描いた図である。
Mayの写像$f_a$で定まる軌道 $\mathcal{O}(f_a; x_0)$ のパラメータ $a$ 依存性はきわめてデリケートな問題であることがわかっている。
