画像相関法(狭義のPIV)
画像中での粒子移動量の算出
画像相関法は、光シートで照明された2次元的な粒子群をビデオカメラ等で撮影し、1時刻目t=t0および2時刻目t=t0+dtにおける粒子画像を得た上で(図2a)、1時刻目の画像における微小な領域(検査領域)内の輝度値分布と2時刻目の画像における領域(探査領域)内の輝度値分布との相互相関関数を求め、その最大値となる位置を検査領域内の粒子群の平均的な移動位置として推定し、変位ベクトルdxを求める方法である(図2b参照)。
相互相関関数は畳み込み演算またはFFTを用いて計算される。検査領域が大きい場合には後者が計算速度において有利である。一方、2時刻の粒子像を1枚のフィルムや撮像素子に2重露光して得られた画像に対しては、自己相関関数が用いられる。
相関法では、時々エラーベクトルが発生するため、その補正が必要である(エラーベクトルの補正参照)。
相互相関関数や自己相関関数は粒子画像と同様に空間的に離散化されているため、求められる変位ベクトルは±0.5画素の誤差を伴う。そこで、離散化された相関関数に二次元正規分布を内挿して連続関数とした上で変位ベクトルを求めることで、誤差を±0.1画素程度に減少させる手法(サブピクセル補間)がとられる。ただし、粒子像の大きさが2画素を下回るときには真の変位量と求められる変位量の関係が線形にならない(ピークロッキング)ので、粒子像の大きさに注意する必要がある。

図2a 1時刻目t=0および2時刻目t=dtにおける粒子画像

図2b 画像相関法のために撮影された粒子画像、相関関数および速度ベクトル分布
物理的な粒子移動量への変換
画像における粒子移動量が求められたならば、以下の方法により物体座標における速度が算出される1)。図3は1台のカメラによって粒子画像を撮影し、速度の2成分を計測する場合を示している。投影関数をFXおよびFYとし、それを時間tで微分すれば
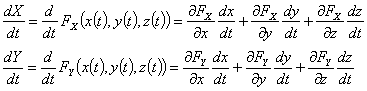
物体座標における粒子速度を
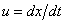
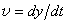
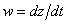 、 、
画像座標における粒子速度(像速度)を
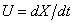
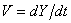
とおいて上式を変形すれば、
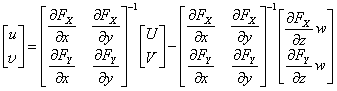
ここで、光シートに対する奥行き方向の速度ベクトル成分wが小さいか、あるいはカメラと光シートが離れており投影関数のzに関する微係数が小さい場合には、右辺第2項をゼロと見なすことで速度ベクトル成分u,vは投影関数の勾配と像速度成分U,Vから求められる。右辺第2項が無視し得ない場合には、次に示すステレオPIVが有効である。
ステレオPIV
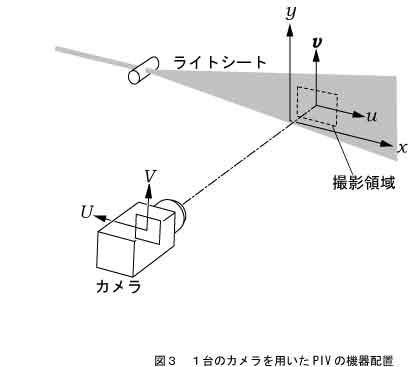
図4のように、2台のカメラによって光シート面内の同一領域を異なる方向から撮影することで、速度ベクトル3成分の2次元分布を計測する方法をステレオPIVと呼ぶ。上付添え字をカメラ番号(1あるいは2)とすれば、像速度は
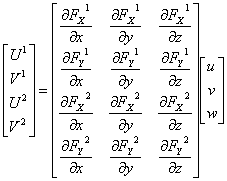
と表される。これを変形してテンソル表示すれば
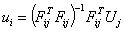
となり、速度ベクトル3成分を像速度および投影関数の勾配から求めることができる。
ステレオPIVは速度3成分の2次元分布を計測する方法であるため、速度の面外方向の微係数を算出することはできない。そこで、ステレオPIVを2セット用いて近接した平行な2断面を計測し、面外方向の微係数を算出することも可能である。これにより、空気噴流発達域の速度勾配テンソル全9成分の二次元的分布が計測されている2)。また、計測面をその面と垂直方向に高速スキャンすることで、速度3成分の3次元的な分布を計測する手法(スキャニング・ステレオPIV)も開発されている3)4) 。
図5は高速カメラと高速パルスレーザを用いたスキャニング・ステレオPIVによる水の軸対象噴流の計測例4)である。噴流コア部分の三次元的な速度ベクトル分布が計測されている。
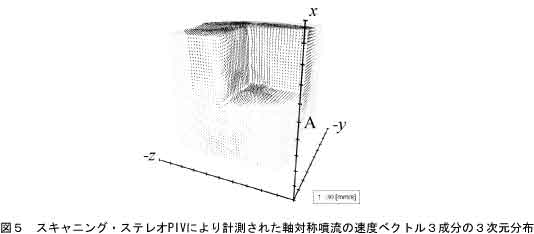
粒子追跡法(PTV)
画像相関法が検査領域内の複数粒子を追跡する方法であるのに対して、粒子追跡法は単一粒子を追跡する方法である。粒子追跡法では、①画像座標における粒子位置の検出、②物体座標における粒子位置の算出、③多時刻にわたる粒子の追跡、の3段階の処理を必要とする。
①の画像座標における粒子位置の検出には、粒子画像を二値化した上で輝度が1の部分を粒子として検出する方法、標準的な粒子像を予め用意しておき、その像と粒子像の相関関数の極大値位置を粒子位置とする方法(粒子マスク法)などがある。
画像座標における粒子位置が求まれば、投影関数に基づいて②の物体座標における粒子位置を求める。1台のカメラで撮影された粒子画像のみを用いる場合には、前項と同様に光シートによって計測領域を2次元面に限定した上で、その面内における2次元的な粒子位置が計測される。一方、体積照明された粒子群を複数のカメラで異なる方向から撮影し、各カメラのピンホールと粒子を結ぶ直線の交点を求めることで、粒子の三次元的位置を得ることができる。
③の粒子の追跡にあたっては、2時刻間dtにおける粒子移動量が平均粒子間距離よりも十分に小さい場合には、各粒子の移動量は1時刻目の粒子の近傍に存在する二時刻目の粒子を探すことで求められる。しかし、粒子移動量が平均粒子間距離と同程度あるいは比較的大きい場合には二時刻の画像から対応する粒子を探すことは困難であり、4時刻の画像に基づいて粒子を追跡する4時刻追跡法5)6)や、複数粒子の配置パタンの類似度から対応する粒子を求める二値化相関法7)、4時刻追跡法と二値化相関法を組み合わせた3時刻パターンマッチング法8)などが用いられている。
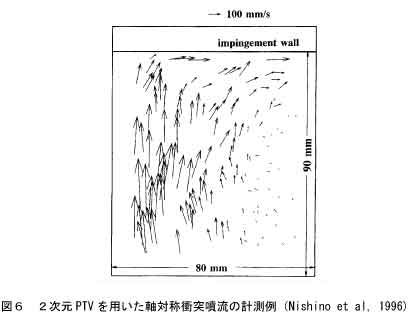
図6は水を作動流体とした軸対称衝突噴流の計測例である9)。カメラ1台を使用して速度ベクトル2成分の2次元分布が計測されている。速度ベクトルの位置は計測時の粒子位置に等しいためランダムに配置される。このため、平均速度分布等の統計量を求める際には、領域を格子状に細分化した上で、各格子内に包含される速度データを統計処理するなどの方法がとられる。
リンク
参考文献
1)可視化情報学会編:PIVハンドブック、森北出版、2002, 172-191.
2)J.A.Mullin, W.J.A.Dahm: Exp. Fluids, 38(2),2005, 185-196.
3)C.Brucker: Appl. Sci. Res., 56(2-3), 1996, 157-179.
4)T.Hori, J.Sakakibara: Meas. Sci. Tech., 15 (6), 2004, 1067-1078.
5)小林敏夫 他: 機論B, 55(509), 1989, 107-114.
6)西野耕一 他: 機論B, 55(510), 1989, 404-412.
7)植村知正 他:可視化情報, 10(38), 1990, 196-202.
8)K.Nishino, K.Torii: Transport Phenomena in Thermal Engineering(J.S.Lee et al. eds.), Begell house, 2, 1993, 1411-1416.
9)K.Nishino et al.: Int. J. Heat Fluid Flow, 17 (3), 1996, 193-201.
|