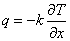
熱流体の数値シミュレーション(CFD)は,電子機器の設計をはじめ各種機器の設計から,台風の進路予想などの天気予報にも重要な役割を果たしている。 本実験では,伝熱の三形態のうち熱伝導を取り上げ,熱伝導に関する理解を深めるとともに,コンピュータを用いて偏微分方程式を解析する方法を学ぶことを目的とする。
物体内に温度勾配が存在すると,高温部から低温部へ熱伝導(Conduction)により熱エネルギーが伝わる。 単位面積あたりの熱エネルギーの移動量である熱流束 q W/m2 は,フーリエの法則により次のように表現される。
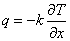
k W/(m・K) は熱伝導率 (Thermal conductivity) であり,物質によって定まる物性値である。 熱エネルギーは温度の高いところから低いところへ向かって伝わるが,このとき温度勾配は負となる。 そこで,フーリエの法則では,右辺にマイナスがつく。 温度勾配が等しい場合,熱伝導率k が大きいほど熱流束q も大きくなり,熱伝導率が大きいと熱エネルギーがよく伝わり,熱伝導率が小さいと熱エネルギーを伝えにくいことがわかる。 ここでは,熱伝導率には記号k を用いるが,λ も一般には広く用いられている。
熱伝導の基礎微分方程式は,フーリエの法則から物体内の微小体積に関する熱エネルギーの収支を考える事により導くことができる。 直交座標における熱伝導方程式は,
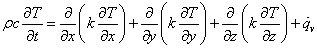
となる。また,熱伝導率k が一定とみなせる場合,熱伝導方程式は,
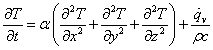
となる。ここで,α = k / (ρc ) m2/s は,熱拡散率 (Thermal diffusivity) と呼ぶ。
導かれた熱伝導方程式は,初期温度および境界条件が与えられると解くことができる。
しかし,解析解を求めることができるのは,形状が単純で境界条件が簡単な場合に限定される。
実用になる複雑な形状や時間変化するような場合などでは,解析解をえることは難しく,多くは数値計算により検討されている。
熱流体現象のシミュレーションを行う場合,現象を表した偏微分方程式を差分法 (Finite difference method) により数値的に解く手法が広く用いられている。
例として,一次元非定常熱伝導問題で考えよう。
図1に示したように,厚さ2Lの無限に広い板が一様な温度20℃に保たれている。
この板の表面を時刻t = 0で急に温度0℃まで冷却する。
このとき,板内の非定常温度分布を求める。
この熱伝導を表す式は,次式で与えられる。
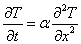
また,初期条件および境界条件は,
t = 0 で,T = 20
t > 0, x = -L, L で,T = 0
コンピュータは,実際の温度や座標といった連続した値を扱うことができない。 そこで,数値計算を行うためには,とびとびの値(離散値)で考える。 座標x 方向に等間隔(Δx)にいくつかの場所を選ぶ。 ここで選ばれた場所のことを,格子点(Grid point)と呼ぶ。 基準となる格子点を i,その両隣をそれぞれ i-1,i+1 とすると,各点における温度を,Ti-1,Ti,Ti+1 と表記する。 また,時間間隔を(Δt )とし,時刻 t = n における温度を,Tnと表記する。
式(4)の時間微分の項は,次のように近似できる。
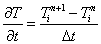
また,式(4)の2階微分の項は,次のように近似できる。
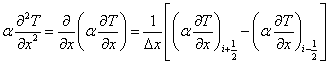
さらに,位置 i-1/2,i+1/2 における微分を Ti-1,Ti,Ti+1 を用いて表せば,
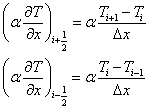
式(4)は,式(5)および式(7)を用いて,次の様に近似できる。
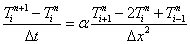
または,
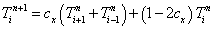
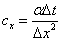
となる。 この式は,未来の温度 Tin+1 を現在の温度 Ti+1n, Tin, Ti-1n で表現できることを示している。
2020.06.23 更新