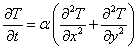機械工学実験２　実験Ｇ（2020年度　春学期）

二次元定常熱伝導

次に，二次元非定常熱伝導問題を考えよう。

図2に示したように，たて・よこL （厚さ方向は考えない）の板が一様な温度20℃に保たれている。 この板の表面上の一点を時刻t = 0で急に温度0℃まで冷却する。 このとき，板内の非定常温度分布を求めたい。
このような二次元非定常熱伝導現象を表す式は，次式で与えられる。

二次元になると，x 方向を i ，y 方向を j を用いて表すと，基準となる格子点とその回りの点の温度は，次の表のように表記する。

この表のイメージをエクセルを用いて具体的に解いてみよう。

1. 定数の設定
   各定数を，それぞれ，セルB1からセルB4に入力する。
2. 初期条件の設定
   セルD4に時刻の初期値（0）を入力する。
   初期温度（20）を，セルD5からセルO16（12×12セル）に入力する。
   内側の10×10セルを，「外枠太罫線」で囲み，「条件付き書式」を設定する。
3. 計算の準備
   D列からO列をコピーし，Q列からAB列に貼り付ける。
4. 計算式の設定
   セルQ4に　=D4+B2　を入力する。
   セルR6に差分化した式を入力し，この式をコピーしてセルR6からセルAA15まで形式を選択して貼り付けで数式を貼り付ける。
   =$B$4*(D6+F6+E5+E7-4*E6)+E6
5. 境界条件の設定
   セルQ5からAB16に，境界条件を設定する。例えば，セルV10，V11，W10，W11に（0）を設定する。
6. 繰り返し
   Q列からAB列を選択してコピーし，D列からO列へ，形式を選択して貼り付けで値を貼り付ける。
   以降，この作業を繰り返すことにより，時刻を進めていくことができる。

実験課題

• 一次元非定常熱伝導の差分近似を参考に，式(21）を差分近似しなさい。

戻る