第6回　非定常熱伝導

これまで現象（温度分布）が時間により変化しないケース（定常（steady-state））を考えてきました。 今回は，温度分布が時間と共に変化する非定常（unsteady-state）熱伝導を考えます。

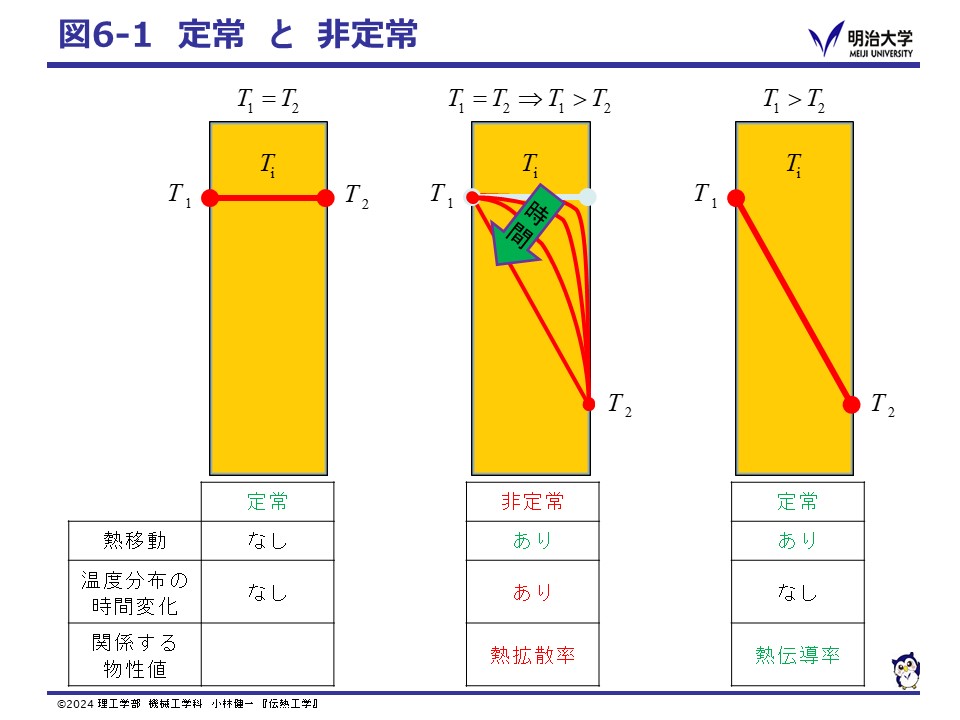
図6-1は，平板を厚さ方向から見た図です。

左の図では，板の両側（T₁, T₂）・内面（T_i）が同じ温度となっており，板を通過する熱の移動はありません。この状態は，定常です。
中央の図は，同じ温度であった板の両側（T₁, T₂）の片側（T₂）を，ある時刻に急に低くした様子です。 板の右側と左側の温度差のため，右側から左側へ熱の移動が生じます。板内部の温度分布は時間とともに図のように変化していくと考えられ，このような状態が非定常です。
片側（T₂）を急に低くしてから時間が経つと，右の図のように板の両側に温度差があり熱の移動は生じていても，板内部の温度分布は時間が経っても変化しなくなります。この状態も熱は左から右に伝わっていますが，温度分布が変化しない状態なので定常です。

定常状態では，物体内に温度分布が存在し熱が移動している場合でも温度の時間変化はありません。このため，現象は熱伝導率にだけ依存します。 一方，非定常状態では，時間とともに各所の温度が変化し物体内に熱が蓄えられたり放出されたりするため，熱容量（密度と比熱の積）および熱拡散率に依存することになります。

このように，非定常熱伝導では，温度分布が時間とともに変化する様子について扱います。

一次元非定常熱伝導

熱伝導率k が一定とみなせる場合の熱伝導方程式は，

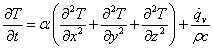
ここでは，一次元の非定常熱伝導現象について考えましょう。

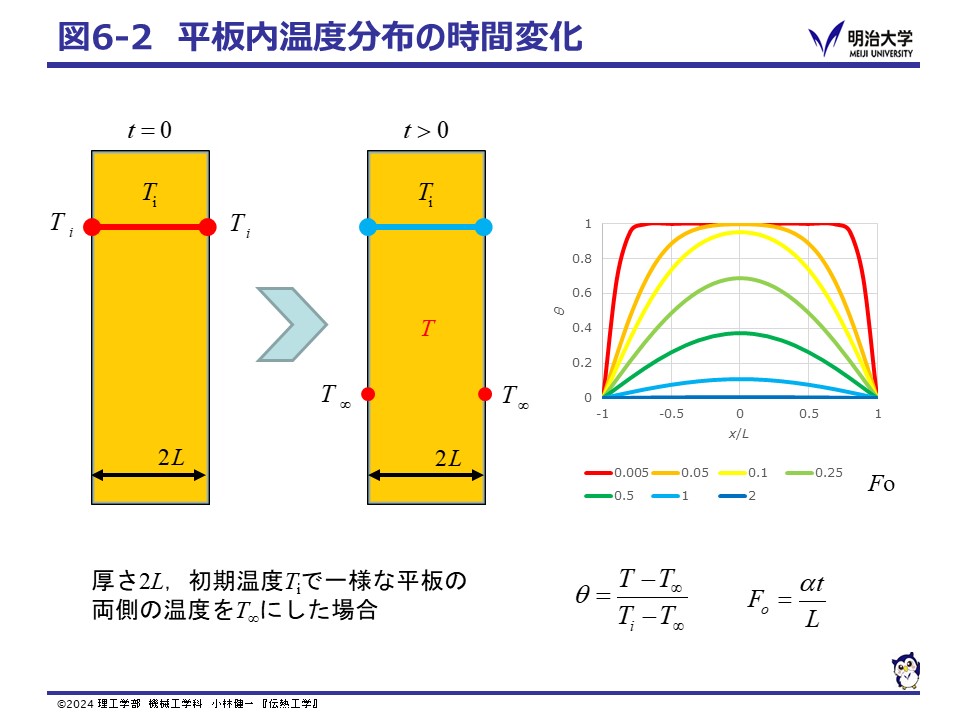
図6-2に示したように，厚さ2L の平板が初期温度 T_i に保たれています。 この板の表面を時刻t > 0で瞬時に温度T_∞にした場合， この熱伝導を表す方程式は，次式で与えられます。

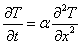
初期条件および境界条件は，

　　　　t = 0 で，T = T_i
　　　　t > 0, x = -L, L で，T = T_∞

この方程式を，変数分離法を用いて解くと，次の解が求まります。

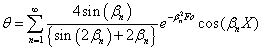
ここで，

， ，

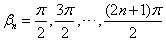
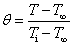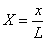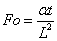
θ は温度差の無次元数を，Foは時間の無次元数であるフーリエ数（Fourier nubber）です。
この解をフーリエ数ごとにプロットしたものが，右の図になります。 時間の経過（フーリエ数の増加）とともに，両側の壁面から板内部へ熱が伝わっていく様子がわかります。 ここで，温度差の無次元数 θ は1（温度差最大）から0（温度差なし）へと変化していくことに注意してください。

平板が対流にさらされる場合

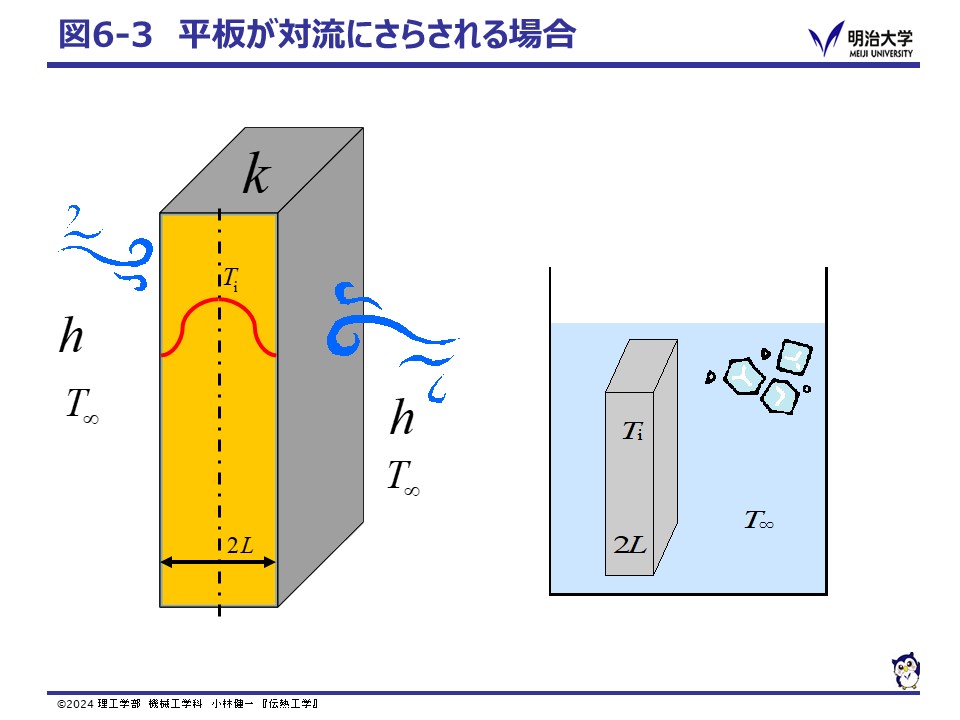
対流にさらされた状態というと，板の周りに風や水が流れている状態を考えますが，空気中や水中に板が静置された場合も 板の周りには境界層といって壁面の温度の影響を受ける領域ができるため，対流にさらされた場合として扱います。 この場合，板内の非定常温度分布は，物体回りの熱伝達率 h と物体内の熱伝導率 k の比である 無次元数ビオ数 (Biot number) Bi によって異なります。

集中熱容量モデル（Bi << 1）

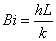
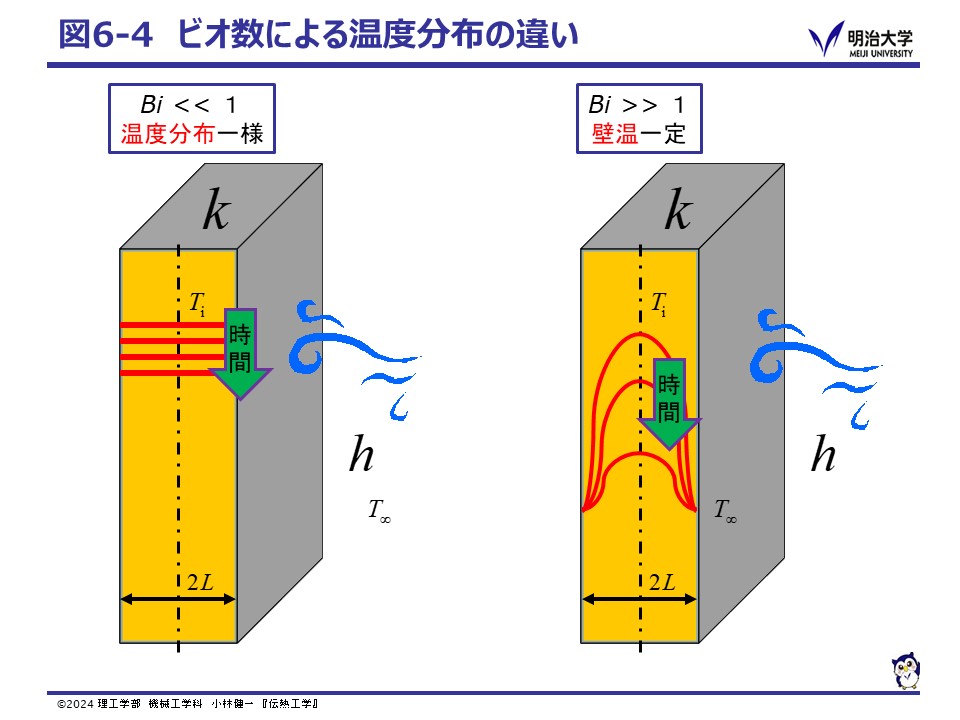
Bi << 1 の場合，つまり，物体の大きさが小さく，熱伝導率が大きい場合，物体内が一様な温度として考えられる 集中熱容量（lumped capacitance）モデルとして扱うことができます。 初期条件 t = 0 で，T = T_i を用いて解くと，次の様になります。

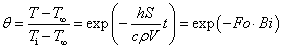
ここで，

壁温一定の場合（Bi >> 1）

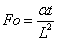
Bi >> 1 の場合，壁面の温度が瞬時に外部の温度となり，壁面の温度が一定の場合として扱えます。 初期条件および境界条件は，

　　　　　t = 0 で，T = T_i
　　　　　t > 0, x = -L, L で，T = T_∞

この条件で解くと，誤差関数（error function）erf(ξ) を用いて解析的に求まります。

ビオ数の影響を受ける場合（Bi ≈ 1）

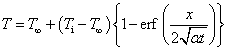
この場合の解は，無限級数の和として解析的に求まります。 計算の手間を省くため，解析結果を線図としてまとめたハイスラー線図（Heisler chart）が用意されています。 ハイスラー線図は，縦軸に平板の無次元中心温度，横軸にフーリエ数をとった図で， 物体の熱伝導率，対流熱伝達率および代表長さが与えられると，平板の中心温度が求まります。

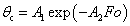
次の表は，式(10) の各パラメータをビオ数について示したもので，ビオ数からパラメータを決定しフーリエ数から平板の中心温度を求める事ができます。

今週の課題

1. （集中熱容量モデル）厚さ 20mm （L = 0.01 m）の十分大きい炭素鋼板が均一温度 800K に十分加熱された後，300K の空気中で冷却される。 空気との熱伝達率を 80W/(m²K) とすると，冷却開始から300秒後の鋼板の温度を求めなさい。 炭素鋼板の熱伝導率は，43W/(mK) ，熱拡散率は，1.18×10^-5 m²/s とする。
2. （ビオ数の影響を受ける）10℃ の冷蔵庫から取り出した厚さ 1cm （L = 0.005 m）の肉を 200℃ 一定のオーブンで焼く。 熱伝達率を 43 W/(m²K) ，肉の物性値をそれぞれ，密度：1100 kg/m³，比熱：3.3 kJ/(kg K)，熱伝導率：0.43 W/(mK)で一定とする。 加熱開始から300秒後の肉の中心温度を求めなさい。