第5回　熱抵抗・多層平板・熱通過

熱抵抗

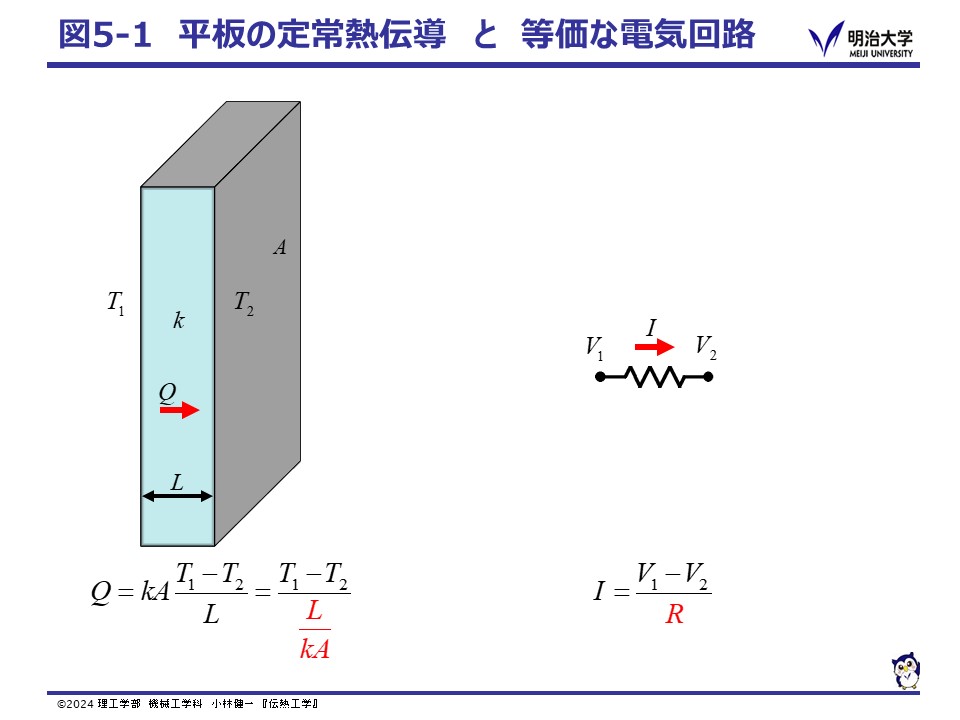
厚さLの平板が， 定常状態で両端の温度が T₁, T₂ のとき， 熱流量は次の様になります。

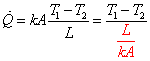
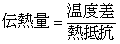
熱の流れを電気の流れ（オームの法則）と相似と考えると， 伝熱量は電流，温度差は電位差にそれぞれ対応していると考えられるので，電気回路の抵抗にあたる概念として 熱抵抗（Thermal resistance） R K/W を考えます。

図5-1の様に，熱の流れを電気の流れと等価回路で考えると， 熱抵抗は，式(1) の分母になっています。

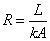
熱抵抗は，直交座標だけでなく，円筒座標や球座標でも定義でき，次の様になります。

円筒座標系の熱抵抗

球座標系の熱抵抗

多層平板

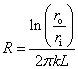
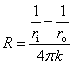
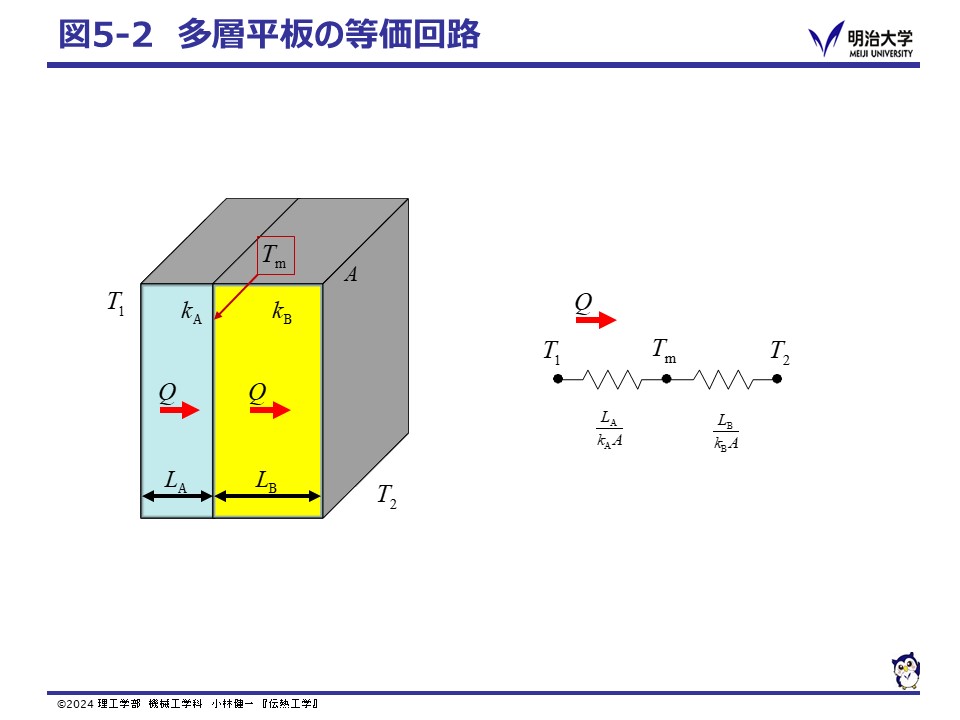
次に図5-2に示したように，厚さ，熱伝導率とも異なる平板が熱の伝わる方向に２枚重なっていて 定常状態で両端の温度が T₁, T₂ のとき， ２枚の平板を横切る熱流は等しく，電気回路の抵抗が直列の場合と同じと考えることができます。 オームの法則において，直列の場合の抵抗値は足し合わせれば良いので， 熱抵抗も同様に考え，熱抵抗を足し合わせたものを用いて，次の様になります。

熱通過

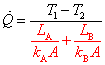
これまで，熱伝導を考える面の境界条件として，温度を規定して進めてきました。 実際の境界条件としては，対流にさらされる場合が多くみられます。
家の壁面や窓ガラス，機器の筐体（ケース）のように，面が流体（風や流水）にさらされている平板を考えよう。

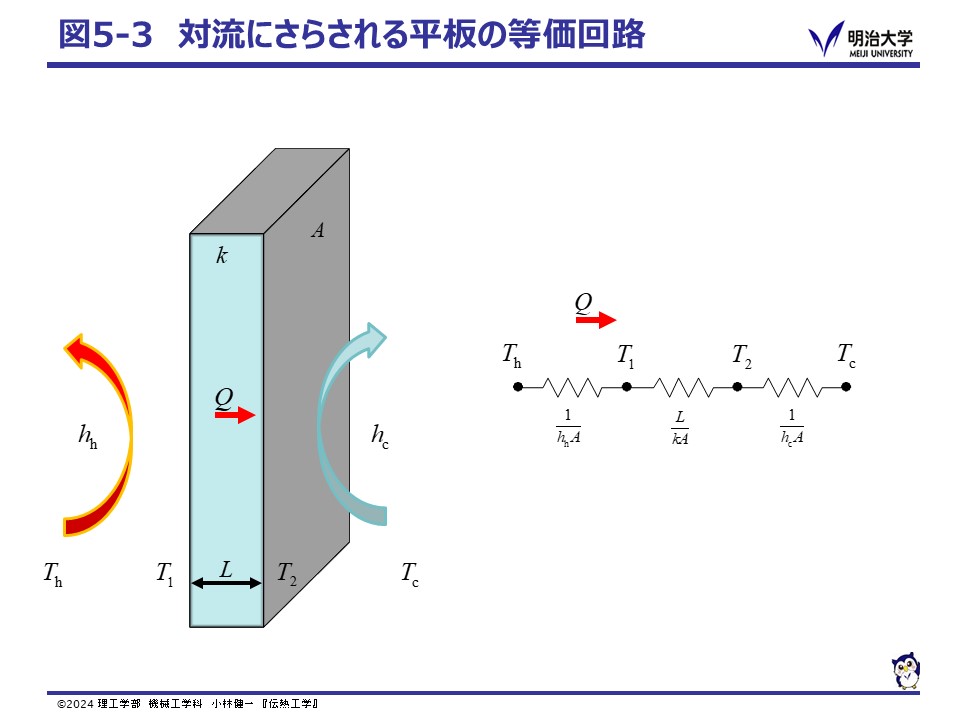
熱流量はどの部分も同じ流れと考えると，次の様になります。

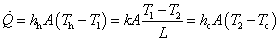
この式を，T_h と T_c の差について求めると， 次の式のように表せます。

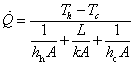
これより，対流にさらされる側の熱抵抗は，対流熱伝達率から次の様に表せる事がわかります。

今週の課題

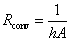
室内側（温度 25℃，熱伝達率 10 W/m²K），外気（温度 0℃，熱伝達率 25 W/m²K）の両面を対流にさらされた厚さ 5.0 mm のガラスの窓（k = 1.0 W/(mK) ）を考える。

1. 室内から外気への損失熱流束を求めよ。
2. ガラスの厚さを2倍の 10 mm にした場合の損失熱流束を求めよ。
3. ガラス窓を「厚さ 2.5 mm のガラスの窓」−「厚さ 2.5 mm の空気層（k = 0.025 W/(mK)）」−「厚さ 2.5 mmのガラスの窓」 と，間に空気層を含む二重ガラスにした場合の損失熱流束を求めよ。