第4回　一次元定常熱伝導

一次元定常熱伝導

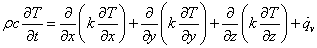
前回導出した熱伝導方程式は，時間・場所・発熱の状態が変数となり，解析により解をもとめることは困難です。

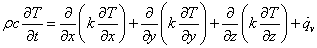
そこで，壁や窓ガラスの様な平板における厚さ方向の伝熱現象について考えてみましょう。

• 十分時間が経過し，温度分布が変化しない　→　時間変化しない
• 温度が一方向（x方向）にだけ変化する　→　y・z方向には，温度勾配がなく一定

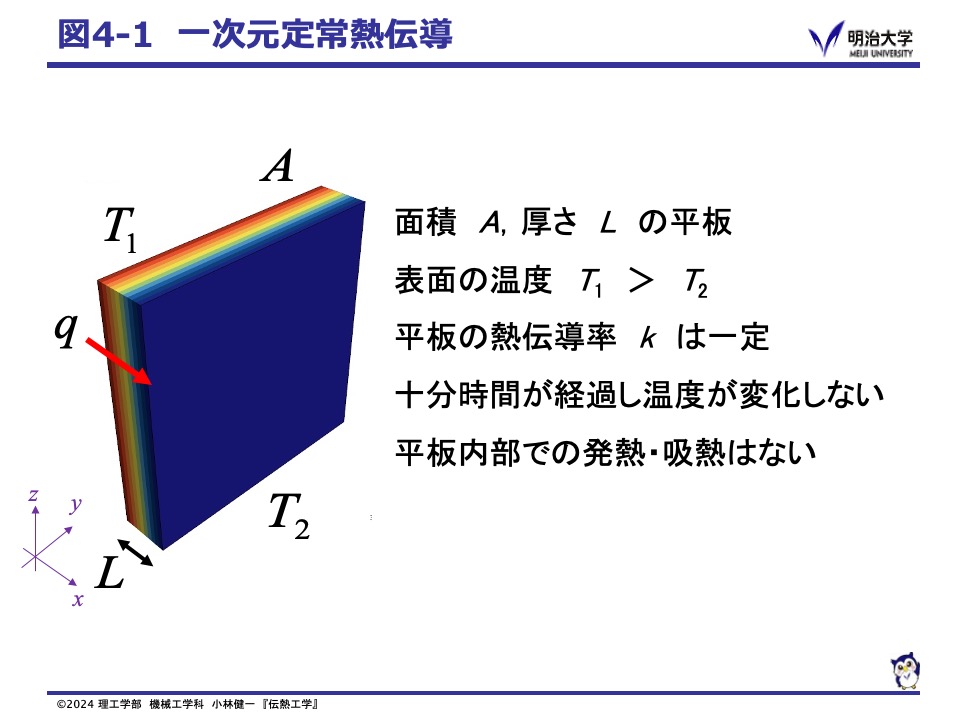
このようなケースを，一次元定常熱伝導 (Steady-state conduction)と呼びます。 このような場合，x 方向の温度勾配のみ考慮すればよいので，熱伝導方程式　式(1)は，偏微分から全微分へと変換できます。

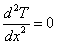
また，境界条件は，

　　　　　x = 0 で，T = T₁
　　　　　x = L で，T = T₂

なので，熱流束および伝熱量はそれぞれ次の様に求まります。

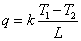
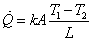
一次元の現象は極端な例のように思えますが，身の回りに起こっている現象でも機器筐体や家の内外の伝熱現象を考えるとき，まずは一次元として扱うことのできるケースが数多くあります。

円筒座標

水筒の様な円筒の内外の伝熱現象も，一見三次元に見える現象ですが，温度は一方向（半径方向）にだけ変化するので，円筒座標を用いることで一次元の熱伝導問題として考えられます。

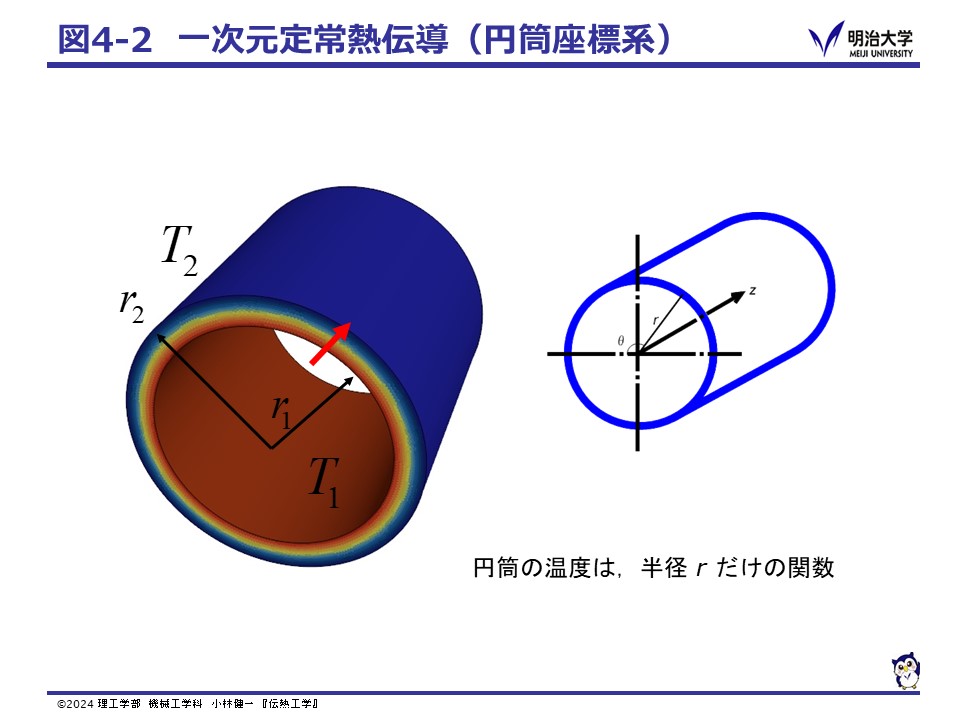
円筒座標系の熱伝導方程式

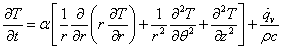
は，このような場合，r 方向の温度勾配のみとなり，全微分の方程式になります。

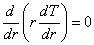
境界条件は，

　　　　　r = r₁ で，T = T₁
　　　　　r = r₂ で，T = T₂

となり，伝熱量は次の様に求まります。

球座標

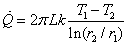
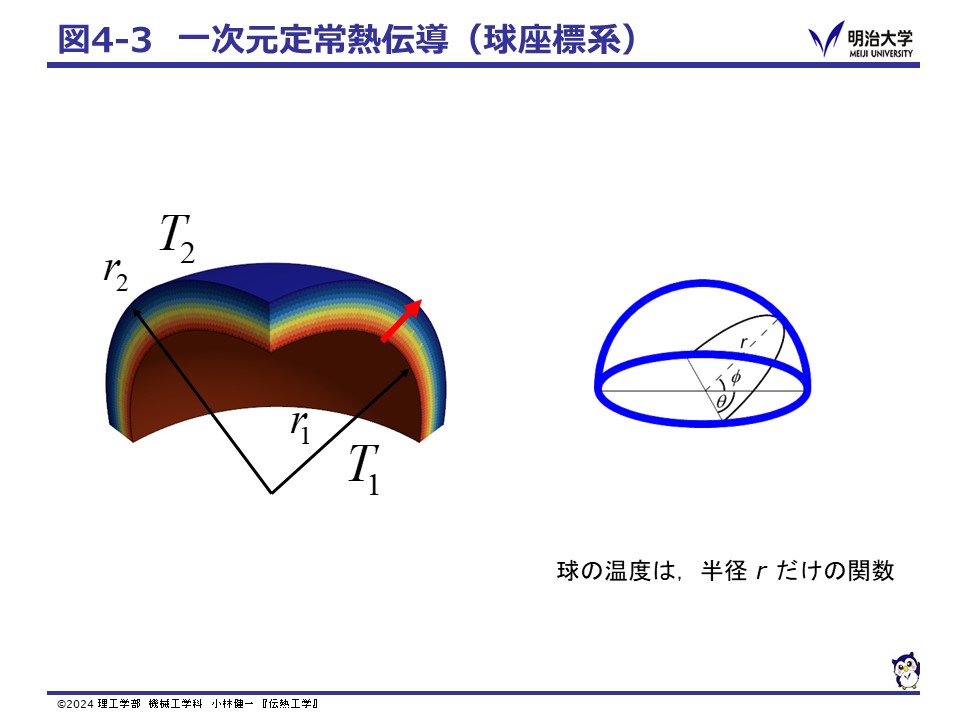
ボールの様な球殻の内外の伝熱現象も，三次元に思える現象ですが，温度は一方向（半径方向）にだけ変化するので，球座標を用いることで一次元の熱伝導問題として考えられます。

球座標系の熱伝導方程式

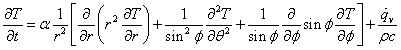
は，このような場合，r 方向の温度勾配のみとなり，全微分の方程式になります。

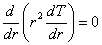
境界条件は，

　　　　　r = r₁ で，T = T₁
　　　　　r = r₂ で，T = T₂

となり，伝熱量は次の様に求まります。

熱伝導の境界条件

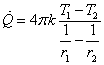
これまで，熱伝導を考える面の条件（境界条件）として，温度を境界条件として規定して進めてきました。実際の場面では，
・温度が定まる場合（温度一定）
・熱流束（熱量）が定まる場合（熱流束一定）
・対流にさらされる場合（対流）
の三種の境界条件が現れます。

熱流束（熱量）一定の場合

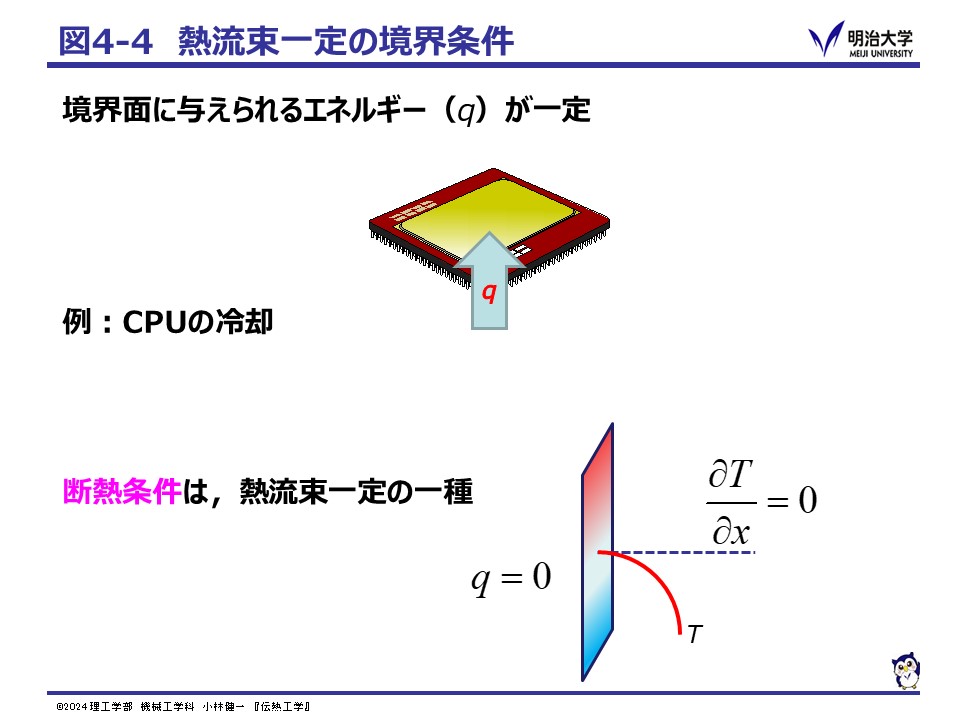
ここでは，熱流束一定の境界条件について見てみましょう。 境界面を通過する熱流束（熱量）が一定の場合とは，電子機器やエンジンなどの冷却が例として考えられます。 壁面の温度ではなく，外部へ伝えなくてはならない熱量（冷やさなくてはならない熱量）がわかっている場合で，熱流束または熱量で与えられます。 この場合，フーリエの法則から，境界面における温度勾配が一定値であることがわかります。

熱流束一定の特殊な場合として，熱流束がゼロ，つまり，熱の移動がない状態が考えられます。 熱流束がゼロの場合を特に断熱 (Adiabatic condition)と呼び，フーリエの法則から断熱の時は壁面の温度勾配が垂直である事がわかります。

熱流束とどちらか一方の面の温度がわかれば，もう一方の面の温度を求めることもできます。