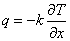
熱の伝わり方のひとつである 熱伝導(Conduction)について詳しくていきましょう。
物体内に温度勾配が存在すると,高温部から低温部へ熱伝導(Conduction)により熱エネルギーが伝わります。 単位面積あたりの熱エネルギーの移動量である熱流束 q W/m2 は,フーリエの法則により次のように表現されます。
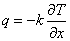
k W/(m・K) を熱伝導率 (Thermal conductivity) と呼び,物質によって定まる物性値です。
熱伝導率k が大きいと,熱流束q が大きくなり熱エネルギーが多く伝わります。
逆に熱伝導率が小さいと,熱エネルギーが伝わりにくくなります。
ここでは,熱伝導率には記号k を用いていますが,一般には λ も広く用いられています。
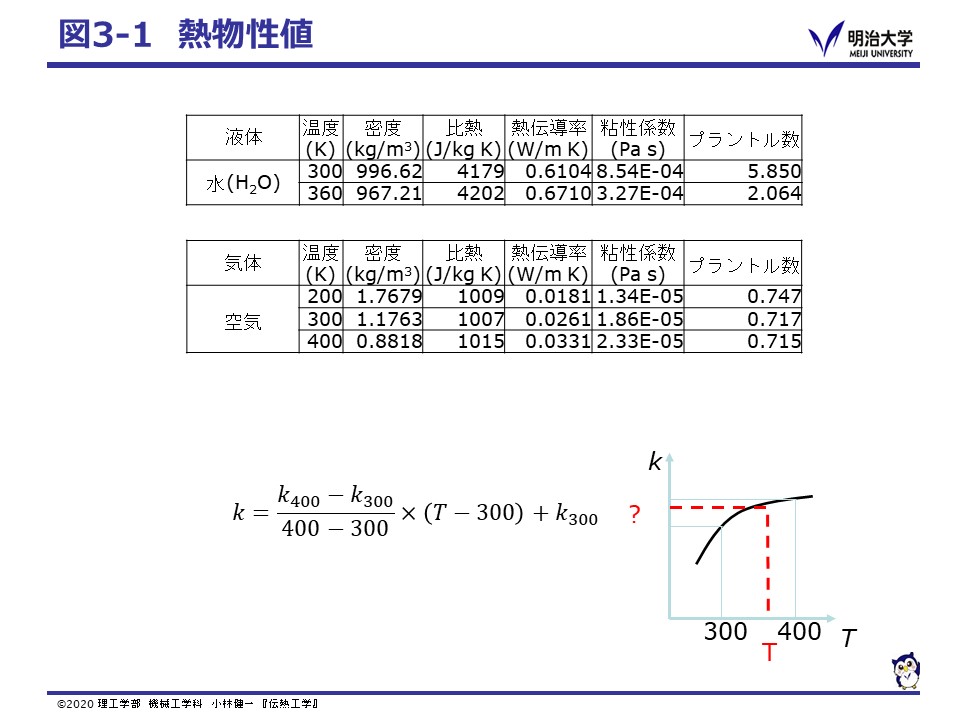
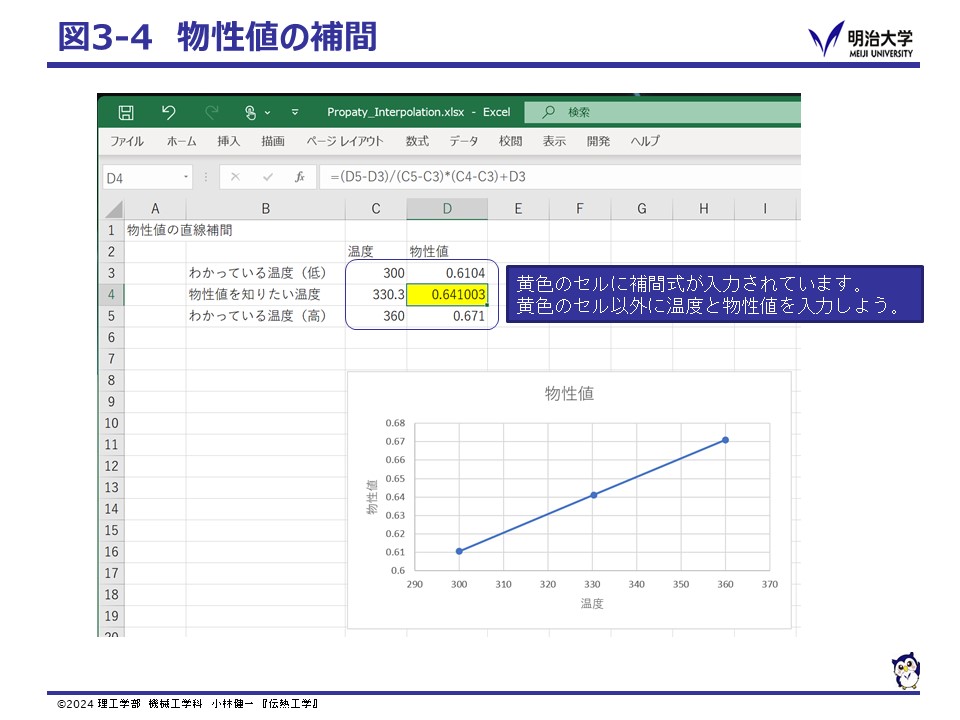
熱物性値は,温度により変化します。 教科書の付録や裏表紙に値が示されていますが,代表的な温度についてのみ示されていて,実際に必要となる温度の値がわからない場合もあります。 このような場合,知りたい温度より低い温度の値と高い温度の値を用い,直線で補間して知りたい温度の値を求めます。
熱伝導の基礎微分方程式は,フーリエの法則から物体内の微小要素に関する熱エネルギーの収支を考える事により導くことができます。
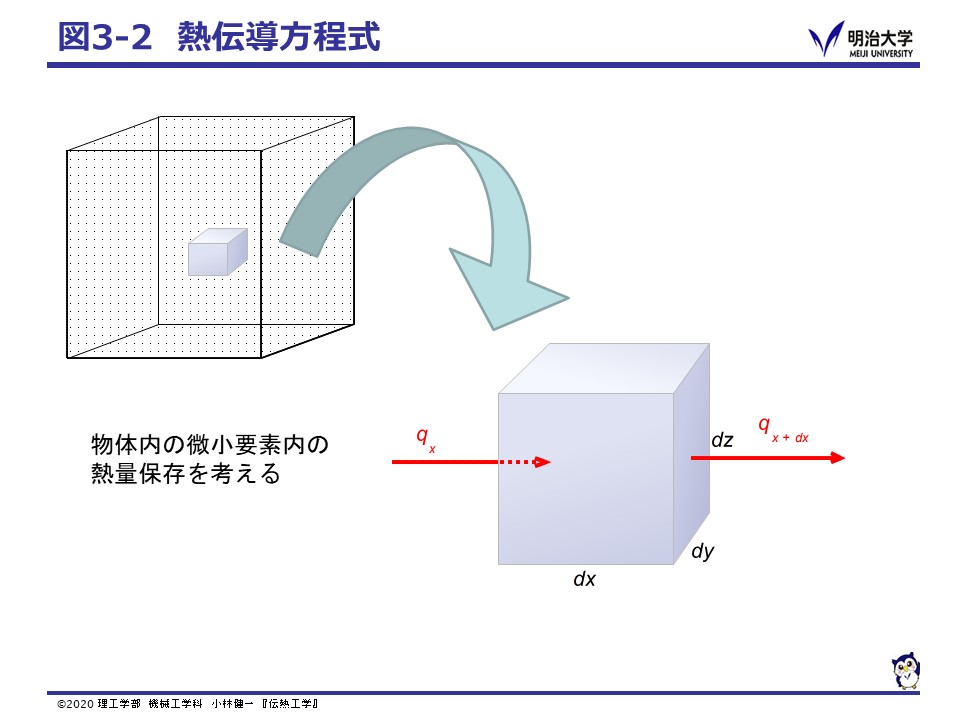
図3-2のように直交座標(Cartesian coordinates system)において微小要素における熱量保存を考えると,
内部エネルギーの変化量 = 熱の流入量 ー 熱の流出量 + 発生した熱量
ここで,各項を式で表すと,
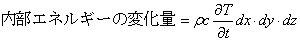
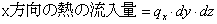

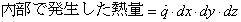
となり,これらを直交座標の三方向全てについて式(2)に代入すると,
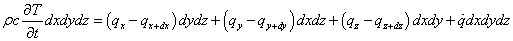
となります。式(7)にフーリエの法則式(1)を適用すると,熱伝導方程式が導かれます。
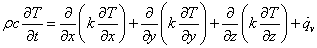
また,熱伝導率 k が一定とみなせる場合,熱伝導方程式は,
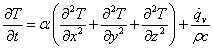
となります。ここで,α = k / (ρc ) m2/s は,熱拡散率 (Thermal diffusivity) です。
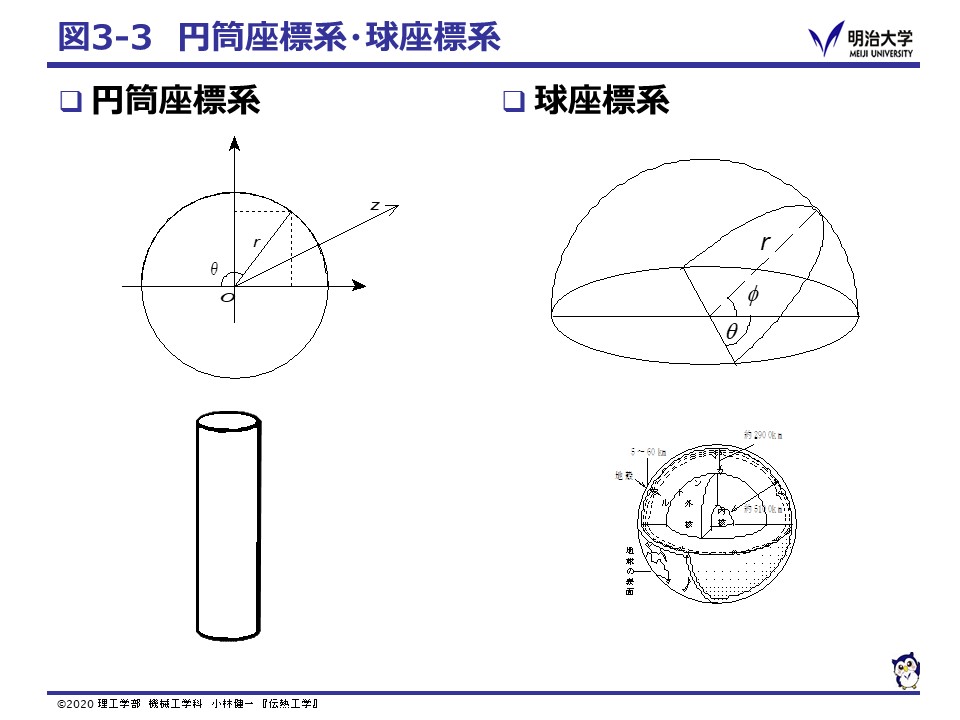
丸棒や電線,パイプなど断面が円で細長い形状の物体を考えるときは円筒座標系(Cylindrical coordinates system),地球などの球体について考える場合には球座標系(Spherical coordinates system)を用いると便利です。 それぞれの座標系で,熱伝導方程式を表すと以下の様になります。
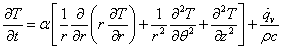
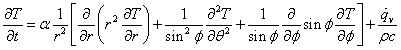
2024.04.25 更新