これまで,熱伝導および対流熱伝達による伝熱について学んできましたが,これらの伝熱様式で
約1億5千万キロ離れている太陽が昇ると地上の気温がすぐ上昇する事を説明できるでしょうか。
?宇宙空間は,ものすごく熱伝導率が高い?
?太陽から地球に向かってものすごく早い風が吹いている?
ここで登場するのが三つ目の伝熱様式であるふく射伝熱 (radiation heat transfer)です。
ふく射伝熱では,熱エネルギーが電磁波として伝わります。
ここでは,まず物体から電磁波が放射される事(ふく射)を学び,その後,電磁波による伝熱(ふく射伝熱)について学びます。
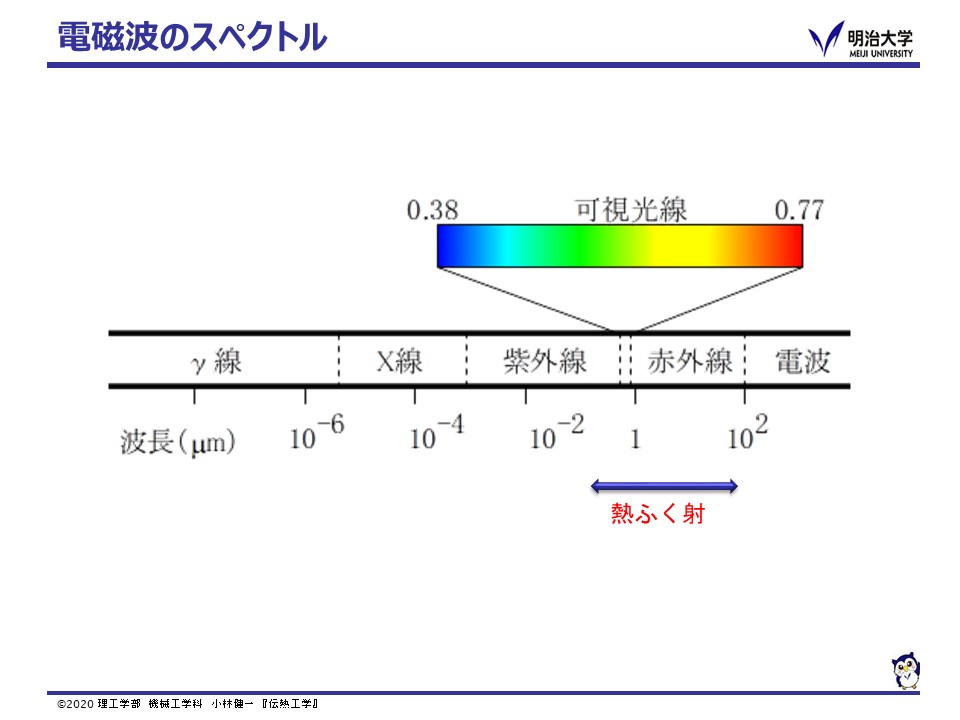
電磁波はその波長により分類され,光速 3.0×108 m/s で伝わります。 熱ふく射(thermal radiation)も電磁波の一種で,その波長は,0.1 〜 100 µm です。

絶対温度がゼロでない物体は,内部エネルギーを電磁波の形で放出しています。 理想的な放射体である黒体(Black body)について波長と放射されるエネルギー密度の関係は, プランクの法則(Planck's law)により,次の図のように,物体の温度によって変化します。
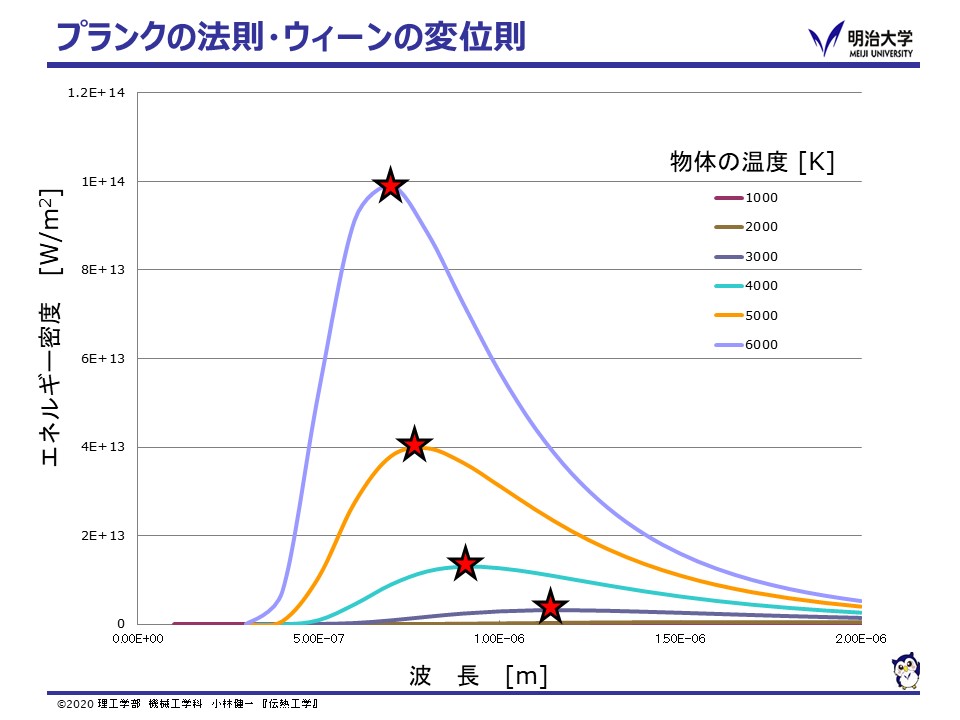
ここでエネルギー密度分布の最大値の波長(図中の星印)は,物体の温度が高温になるに従い短波長になります。ウィーンの変位則(Wien's displacement law)
単位時間・単位面積あたりから放射される全波長のエネルギー Eb W/m2 (上図において,各分布を全波長に渡り積分した値) は絶対温度 T Kの4乗に比例します。ステファン・ボルツマンの法則(Stefan-Voltzmann's law)

ここで,σ はステファンボルツマン定数で,5.67×10-8 W/(m2・K4) の一定値です。放射を扱う場合,温度には絶対温度を用いることに気を付けてください。
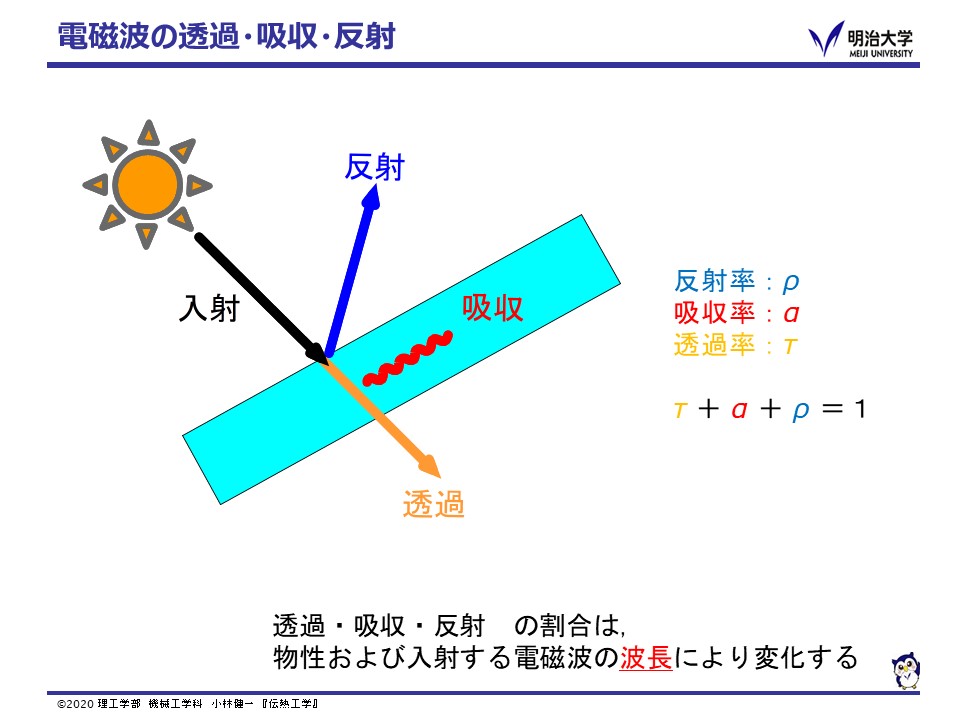
電磁波は物体にぶつかると,図のように一部は反射(refcetion)し,一部は透過(transmission)し,そして,一部は吸収(absorption)されます。 ここで,入射のうち反射する割合を反射率(reflectivity) ρ , 透過する割合を透過率(transmissivity) τ , 吸収される割合を吸収率(absorptivity) α とすると,
ρ + α + τ = 1
となります。多くの固体は不透明なので透過率が0となり,
ρ + α = 1
となります。
先に,黒体は理想的な放射体ですと書きました。ここで,黒体についてもう一度考えましょう。
黒体は,電磁波を100%吸収する(α = 1)事のできる物体です。
ここで,吸収された電磁波のエネルギーはどうなるのでしょう。
やってくる全てのエネルギーを吸収してばかりで,外に放出する事ができなければ,物体の温度はドンドン上昇していってしまいます。
平衡状態を考えると,吸収したエネルギーは,全て放射されると考えられます。このため,黒体は理想的な放射体なのです。
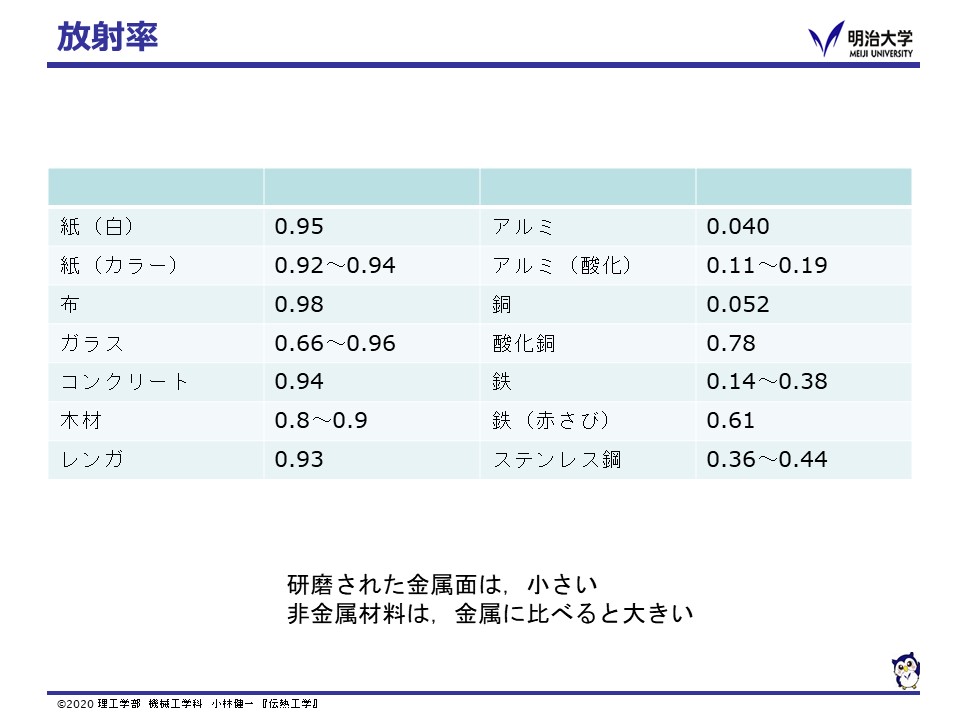
実際の物体表面から放射されるエネルギーは理想的な黒体より小さな値で,その割合を放射率 (Emissivity) ε(0 ≦ ε ≦ 1)とすると,キルヒホッフの法則(Kirchhoff's law)から,放射率=吸収率となります。
ε = α
今回は,太陽定数を求めてみましょう
2024.06.18 更新