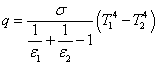
無限に広い二枚の平板が平行に向かい合っている状態を考えましょう。 平板の表面が黒体の場合,一方の平板表面から放射されるエネルギーは,すべて向かい合っている平板へ吸収されます。 このとき,一方の平板の表面温度を T1 K,他方の平板の表面温度を T2 K とすると,平板間の熱流束は,
q = σ ( T14 - T24 )
となります。では,平板の表面の放射率が 1 ではない場合はどうなるでしょう。
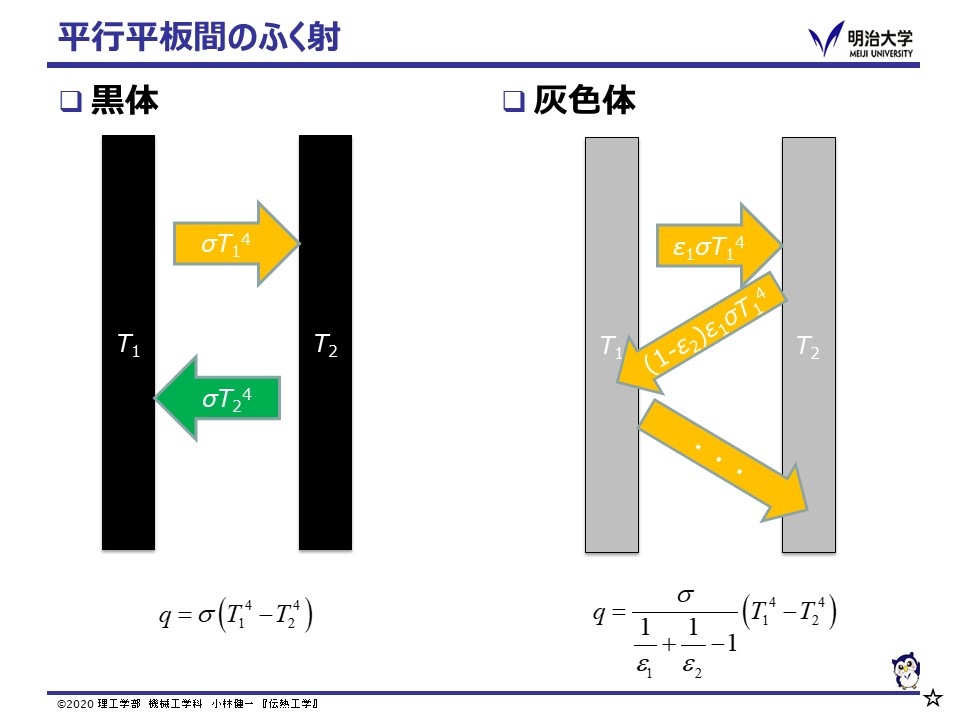
放射率が波長に依存せず 1 ではない表面を灰色(Gray)といいます。 灰色面では,ふく射をすべて吸収することはできず,一部を反射します。 面1から放射されたふく射は,面2では一部が吸収され残りが反射されます。 面2で反射されたふく射は,今度は面1で一部が吸収され残りが再度反射されます。 このように灰色の面同士では,多重に反射を繰り返します。 多重の吸収・反射の総和をとると,灰色な平行平板間の熱流束は次のようになります。
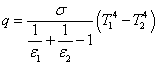
前回の演習では,太陽から放射される総エネルギー量と,地球の軌道上で単位面積に届く量を求めました。 このように実際の物体間では,一方の面から放射されたふく射のうち一部だけが他方の面に届きます。 そこで,一方の面から放射されたふく射のうち他方の面に届いた割合を,形態係数(view factor)と定義します。

形態係数とふく射する面の面積の間には,次の関係が成り立ちます。
A1F12 = A2F21
形態係数を用いると,有限の大きさの物体間のふく射による伝熱量は,次のようになります。
q12 = F12σ ( T14 - T24 )
ここで,前回求めた太陽からのふく射を用いて,形態係数について考えてみましょう。
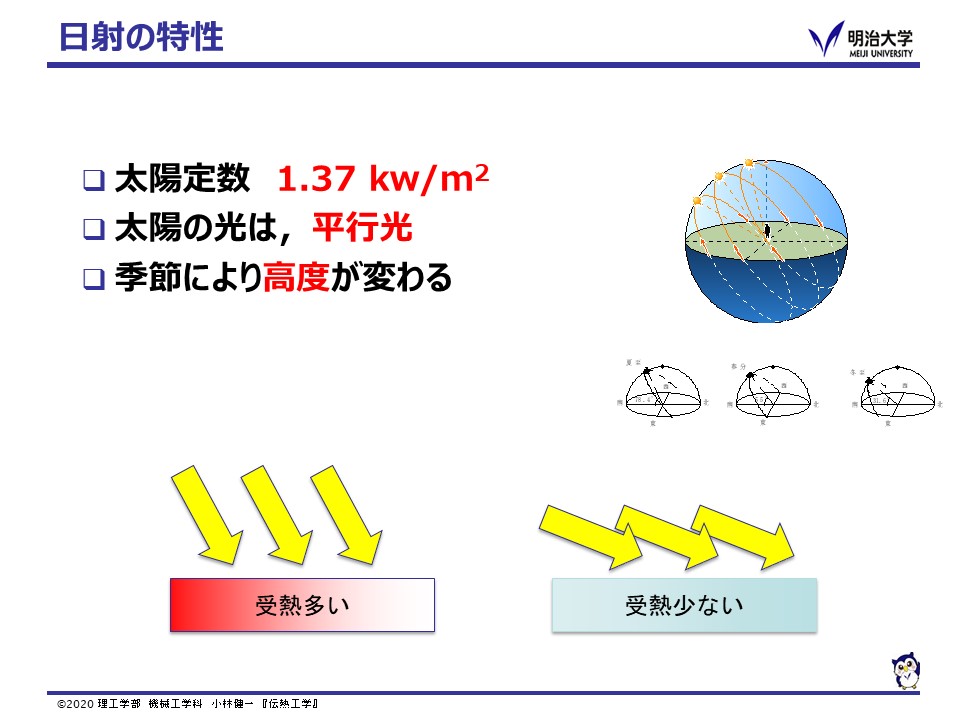
太陽(球体)から四方に放射されたふく射は,十分に遠く離れた地球の軌道上では平行光と近似できます。
太陽に正対した面では,(大気を無視すると)前回求めた太陽定数の熱流束が太陽から届きます。
しかし,地球は太陽に対し傾いて公転しているので,地上では季節により太陽高度が変化します。
水平面の場合,冬より夏が太陽高度が高くなり,単位面積あたりに太陽から受けるふく射熱流束は大きくなります。
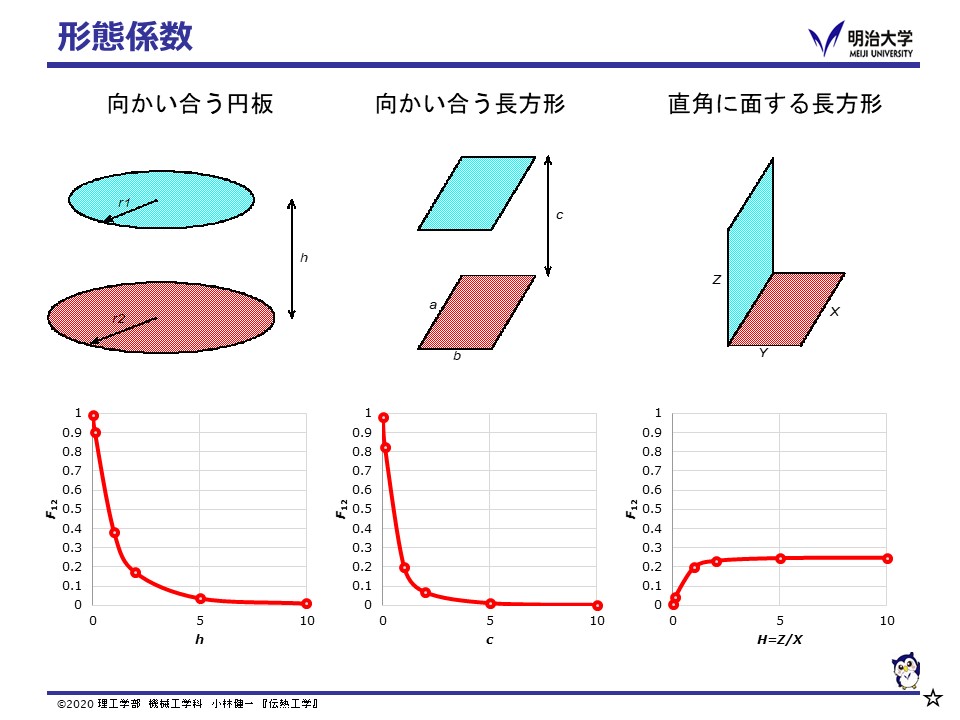
太陽と地球の例のように,形態係数は,単純な形態では立体角(ステラジアン)を用いて幾何学的に求めることができます。 しかし,実際の複雑なものについては線図が用意されています。
これまでは,固体表面のふく射による伝熱を考えてきました。
地球温暖化で注目される二酸化炭素などの気体の場合は,ふく射による伝熱は起こるのでしょうか。
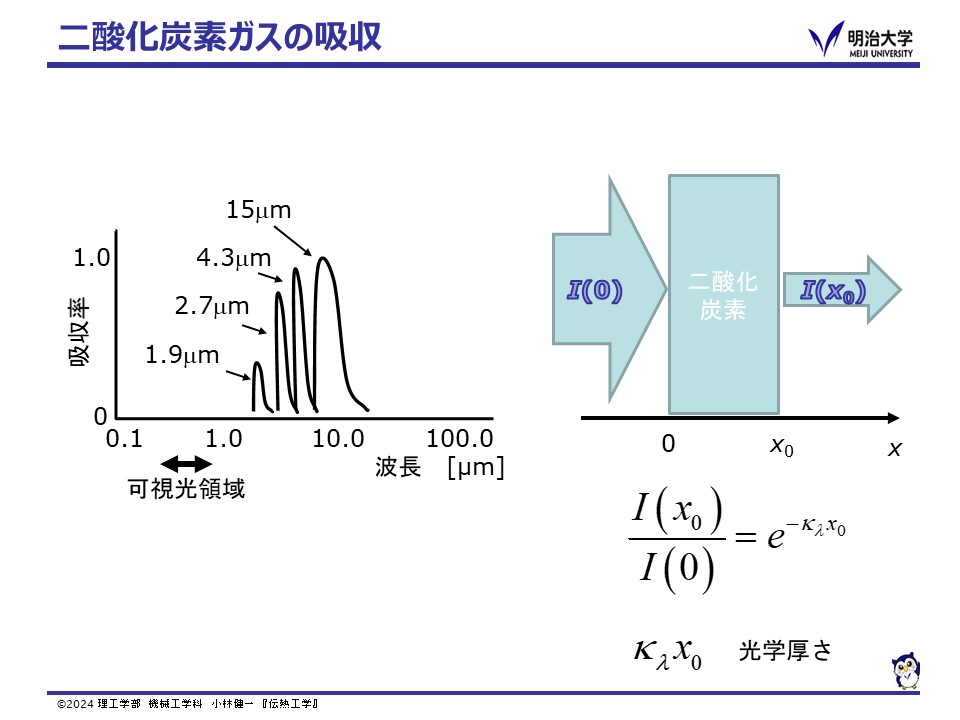
気体(ガス)の場合,固体の様に表面ではなく,気体中を通過するときに吸収・放射が起こります。
このため,特定の波長領域(吸収バンド)に限り吸収する選択吸収性があります。
また逆に,気体からは特定の波長のみふく射されます。
壁面から流体への伝熱を考えると,ふく射伝熱が単独で生じることは少なく,対流熱伝達と併せて生じます。 そこで,ふく射伝熱と対流熱伝達を合計した伝熱量が重要になります。 ふく射による伝熱は,表面の状態や相互の位置関係に大きく依存し複雑なので, 対流熱伝達によるニュートンの冷却法則
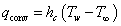
と形式を合わせ,ふく射熱伝達率(radiation heat-transfer coefficient)を定義し,
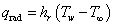
対流熱伝達とふく射伝熱を合わせた総合熱伝達率とし,ふく射伝熱を含めた伝熱量を求めます。
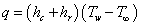
多くの場合,対流熱伝達率は温度の影響をあまり受けませんが, ふく射熱伝達率は高温になると急激に高くなり,全伝熱量に占めるふく射伝熱の割合が大きくなります。
2024.07.04 更新