第9回　自然対流熱伝達

自然対流

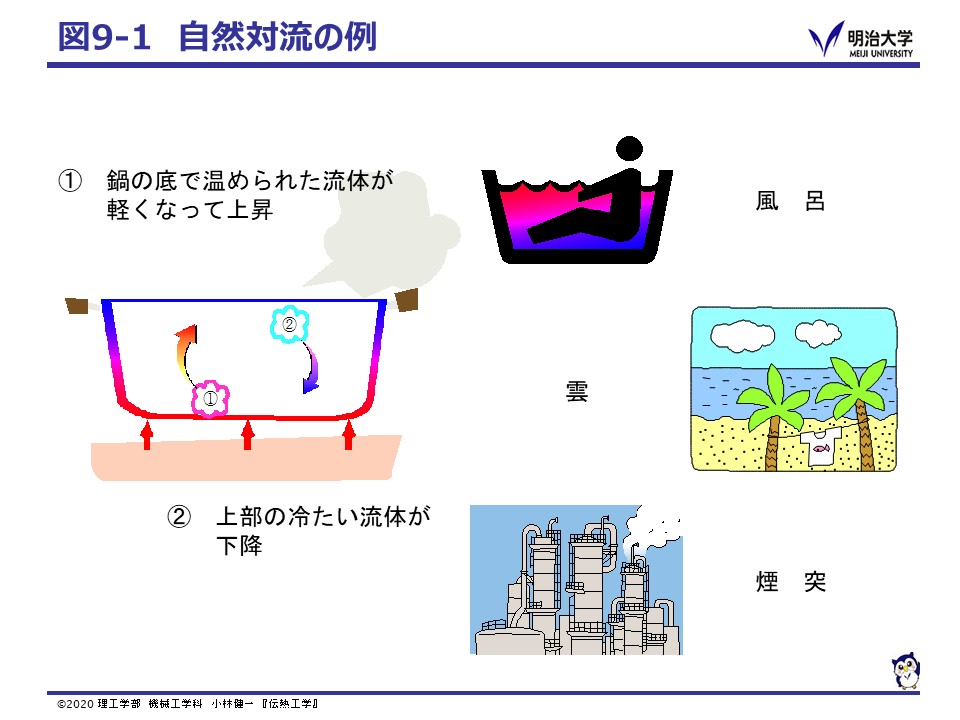
重力の向きに温度差があると，浮力（buoyancy）が生じます。 これは，流体は多くの場合，高温になると密度が下がりより軽く，低温になると密度が上がりより重くなるためです。
また，気体と液体が接する界面では，表面を小さくしようと表面張力（sufrface tension）が働きます。 液体表面の温度や濃度にばらつきがあると，表面張力が不均一となりマランゴニ効果（Marangoni effect）が働きます。
このように，温度差に起因する浮力や表面張力などにより対流熱伝達率が生じる現象を，自然対流（natural convection）と呼びます。

浮力

周囲の温度 T_e 中で温度 T の流体が受ける単位体積あたりの浮力は，

ここで，密度と温度の関係から体膨張係数（volumetric thermal expansion coefficient） β 1/K を次の様に定義します。

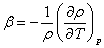
通常の気体の場合は，絶対温度（注意！）の逆数と近似できます。

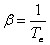
この体膨張係数を用いると，浮力は，

と表されます。

垂直に置かれた平板のまわりの自然対流

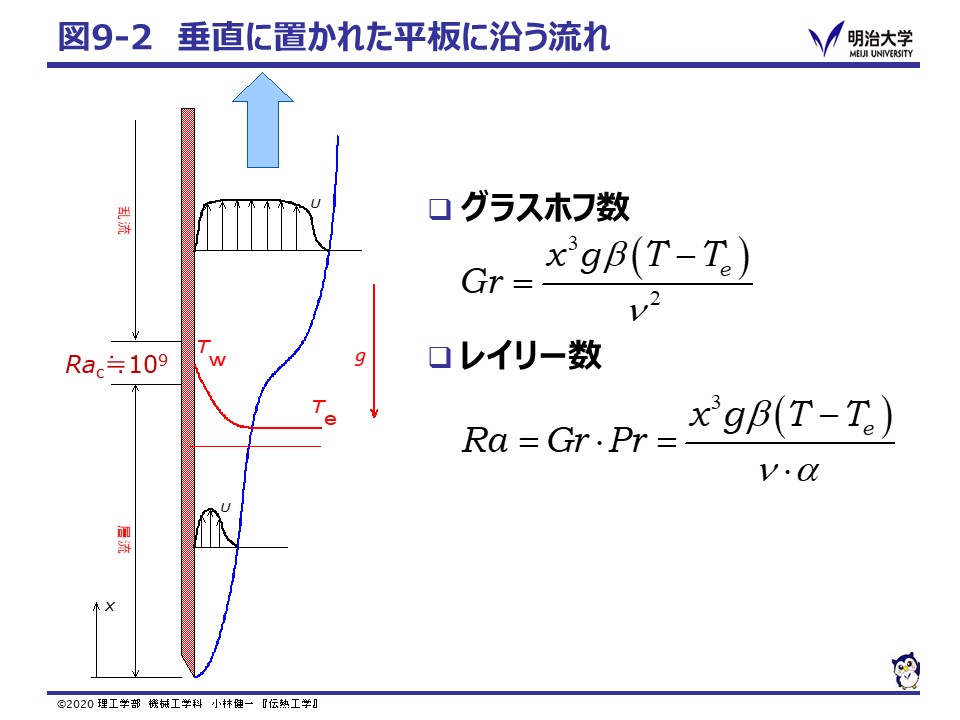
周囲の温度 T_e の静止した流体中に，垂直におかれた温度 T_w に加熱された平板のまわりに生じる対流を考えましょう。 流体は当初静止していますが，加熱された壁面のまわりの流体がしだいに暖められ，周囲の流体に比べ低密度となり上昇をはじめます。 このため，加熱された平板のまわりに上昇する流れが生じ，速度分布は図9-2の様に，壁面の近くに上向きの流れが生じ，平板から離れた所では温度分布がなく流体は静止したままとなります。 また，壁面に沿って上昇していくうちに，強制対流の場合と同様に流れは層流から乱流へと遷移します。

ここで，壁面付近で働く浮力と粘性力の比から，グラスホフ数（Grashof number）とレイリー数（Rayleigh number） を考えると，層流から乱流への遷移は，レイリー数が 10⁹ 程度となる地点で起こります。 垂直平板の全長に対する平均熱伝達率の相関式としては，次の式が知られています。

水平に置かれた平板のまわりの自然対流

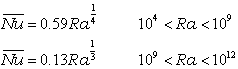
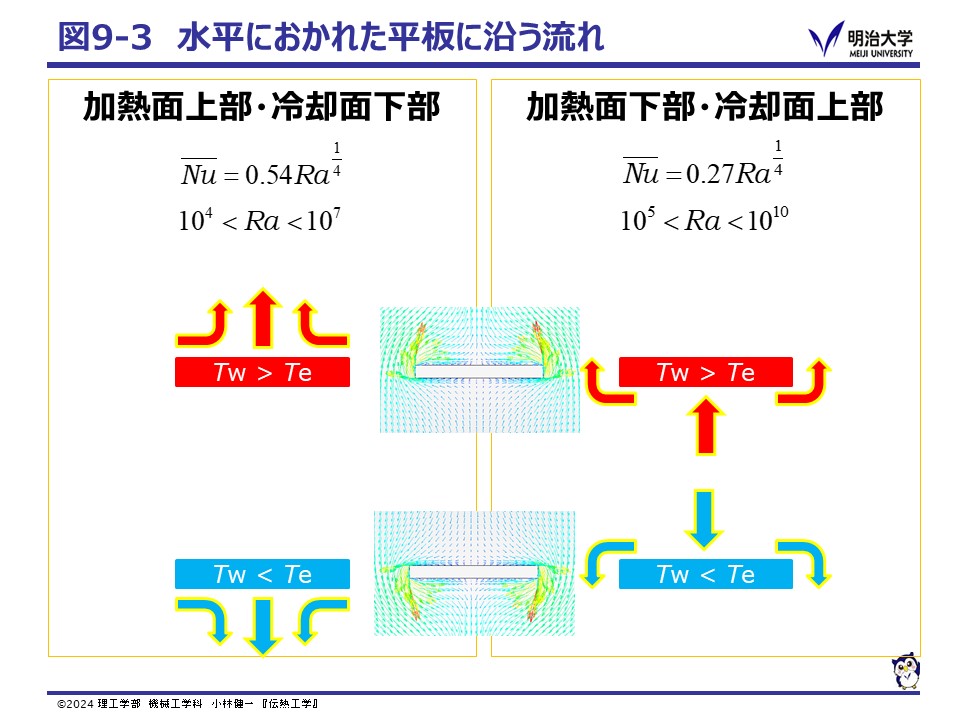
次に，周囲の温度 T_e の静止した流体中に，水平におかれた温度 T_w に加熱された平板のまわりに生じる対流を考えましょう。この場合，自然対流は，数学的に

1. 加熱面上部・冷却面下部
2. 加熱面下部・冷却面上部

の二つの場合に分類されます。 水平平板の全長に対する平均熱伝達率の相関式としては，次の式が知られています。