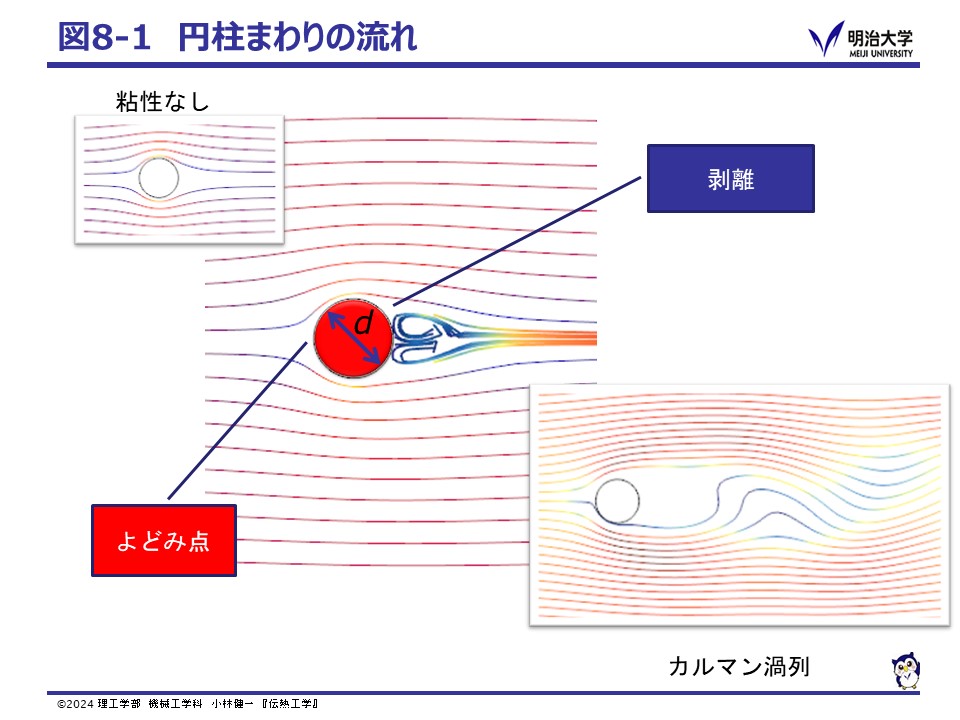
一様な流れの中に置かれた物体まわりの流れを外部流れと呼び， 前回の平板をはじめ，円柱・球・円管群などの外部流れに関しての伝熱相関式が提案されています。 ここでは，外部流れを代表して，円柱まわりの流れと対流熱伝達について確認します。
粘性の非常に小さい場合，円柱の前後で流れはほぼ対称となります。
実際の流体には粘性があるため，円柱前面から後面へ向かう途中で剥離が生じ，
円柱後流に対になる渦が形成されます。
さらに流速を早めていくと，渦が交互に周期的に放出されるようになります。
このように周期的に放出される渦をカルマン渦列と呼び，自然界でも観察することができます。
加熱された円柱に冷たい流体が当たる場合，上流のよどみ点が最も高い熱伝達を示し剥離点へ向かって熱伝達率が低下していきます。
流れに置かれた円柱まわりの相関式は，流れの状態に応じて細かく分類されています。
ここで，円柱からの伝熱量を前回の平板と同じような寸法・温度・流速で具体的に計算してみましょう。 直径 200 mm，幅 100 mm の円柱に温度 Te = 20 ℃，常圧の空気が 8 m/s で流れているとき， 円柱の温度が Tw = 100 ℃ 一定の時，円柱からの伝熱量を求めよう。
円柱まわりの流れの場合，代表長さには円柱の直径を用います。
物性値を求めるための温度は，平板と同様に膜温度を用います。
円柱流れのレイノルズ数は，
このレイノルズ数における平均ヌセルト数の式は，
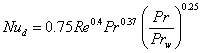= 205.6
平均熱伝達率は，
したがって，伝熱量は，
と求まります。
管内を流れる流体など壁で囲われな内部の流れを内部流れと呼び， 円管，平行平板間などの内部流れの伝熱に関して相関式が提案されています。 ここでは，内部流れを代表して，平行平板間・円管内の流れと対流熱伝達について確認します。
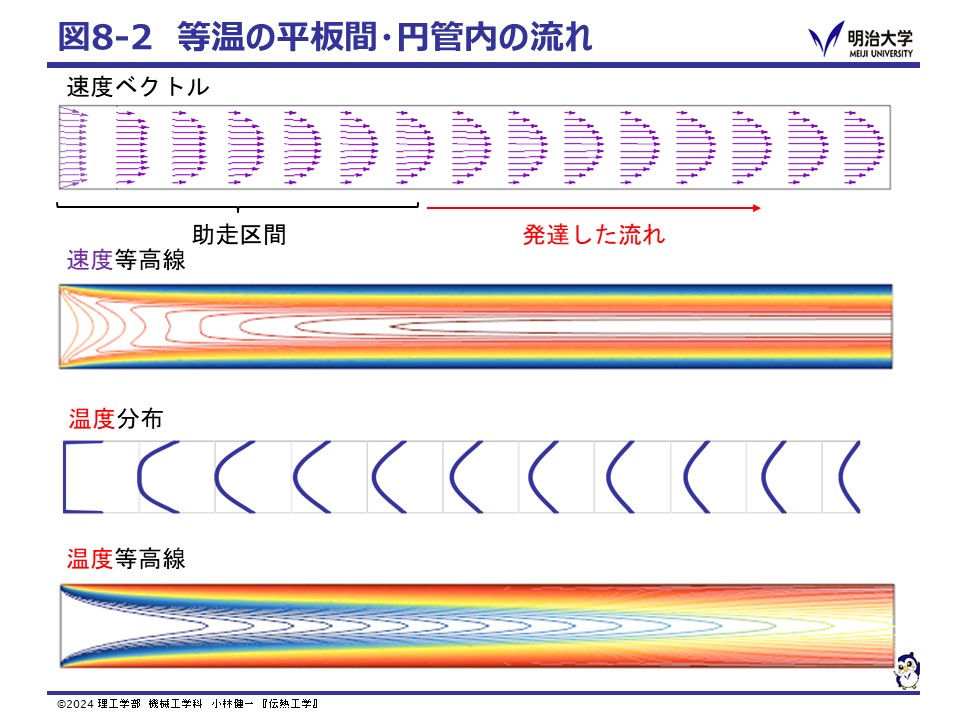
一様な流れが管内に流れ込むと，境界層がまわりの壁から中心へ向かって発達していきます。
境界層が徐々に発達している区間を助走区間，
境界層が重なり速度分布が変化しなくなった区間を発達した流れと呼びます。
温度の場合も，速度と同様に温度境界層がまわりの壁から発達します。
温度境界層が重なった地点以降を発達した区間と呼びますが，温度の場合，
発達した区間でも壁面から熱の流入が続くため内部の温度は上昇を続けます。
このため発達した区間の温度分布は，形状は相似ですが壁面と中心の温度差が徐々に小さくなっていきます。
円管内や平行平板間の流れの場合，十分発達した等温加熱状態でヌセルト数は，
円管では3.66，平行平板間では7.54と，一定値に漸近します。
2024.06.18 更新