今回からPython によるプログラミングについて学んでいきますが、 まずは Python の基本的事項のおさらいをしていきましょう。
インタープリタ言語である Python は、C 言語と異なりコンパイル不要です。
プログラムを1行ずつ逐次的に実行していくため、バグの発見・修正がしやすいという特徴があります。
C 言語ではエラーを全て取り除かないとコンパイルできないため、
初学者にとってバグ修正しにくいと感じることもあったかもしれませんが、
Python の場合はエラーがある行までは実行されるのでエラーの場所が明確になります。
(もちろん、エラーが出ていないからといって、バグがないという保証にはなりませんが)
C 言語では、if による条件分岐や for・while による繰り返し、関数の定義を行う際に { }(中カッコ)でコードのブロック化をおこなっていました。 これに対し、Python ではインデント(字下げ)を用いてコードのブロック化をおこないます。
具体例として、第2回で紹介した二分法のプログラムについて、 C 言語と Python の場合を比較してみましょう
// 二分法
#include <stdio.h>
#include <stdlib.h> // exit 関数を用いる為に必要
#include <math.h> // fabs 関数を用いる為に必要
double f(double x); // 関数 f(x) のプロトタイプ宣言
#define A (1.0) // f(A) < 0 となるような A を設定
#define B (2.0) // f(B) > 0 となるような B を設定
#define E (1.0e-10) // 収束判定に用いる
int main()
{
// 使用する変数の宣言
double a, b, c, e, fc;
int i;
// 変数の初期化
i = 0;
a = A;
b = B;
e = E;
// A, B の値の妥当性チェック
if( !( (f(a) < 0) && (f(b) > 0) ) )
{
printf("A, B の値が不適切です。\n");
} else {
// 二分法アルゴリズム
// |a-b| / 2 > e の間繰り返す
while( fabs(a - b) / 2.0 > e )
{
c = (a + b) / 2.0;
fc = f(c);
i++;
// 繰り返しの回数 i と c の値を表示
// %10.8lf とは、全部で10文字、小数点以下8桁で表示するという意味
printf("%d %10.8lf\n", i, c);
// c の符号により a または b に c を代入
if( fc > 0.0 )
{
b = c;
}
else if( fc < 0.0 )
{
a = c;
}
// fc == 0.0 であれば、c は根であるから繰り返し文を強制的に抜ける
else
{
// break 文によって強制的に繰り返し文を抜けることができる
break;
}
} // while 終了
} // if 終了
}
// 関数 f(x) の定義
double f( double x )
{
return (x*x - 2.0);
}
# 関数の定義(x*x-2.0 を計算する関数)
def f(x):
return x*x - 2.0
# 変数の初期化
a = 1.0
b = 2.0
e = 1.0e-10
i = 0
# 初期値a, b の値の妥当性チェック
if not ( f(a)<0.0 and f(b)>0.0 ):
print("a, b の値が不適切です。")
else:
# 二分法アルゴリズム
# |a-b| / 2 > e の間繰り返す
while abs(a-b) / 2.0 > e:
# aとbの中点cとf(c)の計算
c = (a + b) / 2.0
fc = f(c)
i += 1
# 繰り返しの回数 i と c の値を表示
print("i=", i, " c=", c)
# c の符号により a または b に c を代入
if fc > 0.0:
b = c
elif fc < 0.0:
a = c
# fc == 0.0 であれば、c は根であるから繰り返し文を強制的に抜ける
else:
break
Python ではインデントによるブロック化のほかにも、明示的な変数の宣言がない、 論理演算子(and, or, not)の違い、コメント文の書き方など C言語と異なる部分が少なからずあることに注意しましょう。
ちなみに上記のサンプルコード内にはありませんが、繰り返し処理でよく使う for 文も C 言語と Python で違いがあるので注意しましょう。
for(k = 0; k < N; k++) {
printf( "%d\n", k );
}
例えば、上記のようなC 言語での繰り返し処理は Python では以下のように書けます。
for k in range(N):
print( k )
range() 関数の使い方については、他にも以下のようなものがあります。
また、以下のようにリストを用いて繰り返し処理を行うこともできます。
for k in [1,2,3,4,5]:
print( k )
for k in ["red","green","blue"]:
print( k )
Python が初学者にも扱いやすい理由の一つとして、
豊富なライブラリ(Python ではモジュールと呼ぶ)が利用可能な点が挙げられます。
今回学んでいくようなグラフィックの他にも、数値計算や機械学習に関するパッケージも数多く存在しており、
(理論的なところをほとんど理解できなくても)簡単に機械学習などを試すことができます。
この授業では、matplotlib と呼ばれる可視化のためのパッケージを利用していきます。
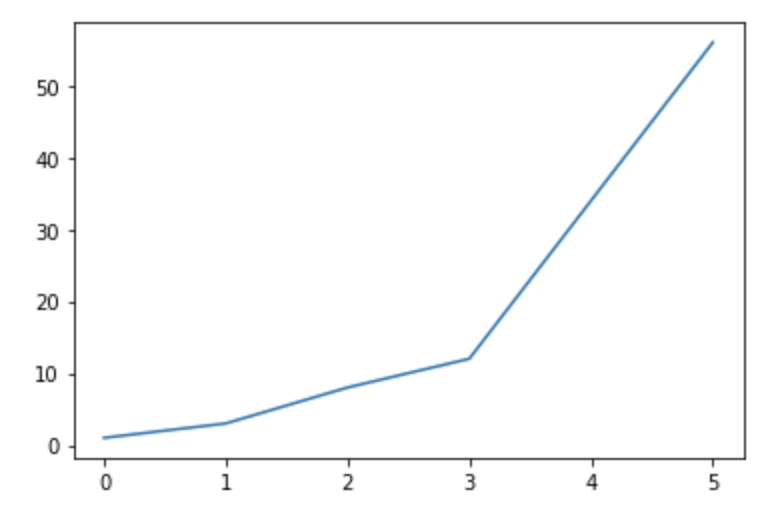
# matplotlibのpyplotモジュールをpltという名前としてインポート import matplotlib.pyplot as plt # グラフを描画するためのデータを格納するリスト a = [1,3,8,12,34,56] # リストa内のデータを折れ線グラフとして描画 plt.plot(a) # グラフの表示 plt.show()
上記のプログラムでは、matplotlib の pyplot というモジュールを用いて、グラフを描画しています。
最初に pyplot モジュールをインポート(C 言語におけるヘッダーファイルのinclude のようなもの)していますが、
その際に plt という名前でインポートしています(as plt の部分)。
こうすることで、以降のプログラム内では plt.xxxx と描くことで pyplot モジュールの関数を利用することができます。
グラフの描画については非常に簡単で、描画するためのデータを格納したリストを用意すれば、
plt.plot() 関数を使って簡単に折れ線グラフを作成することができます。
最後に plt.show() 関数でグラフを画面に描画させます。

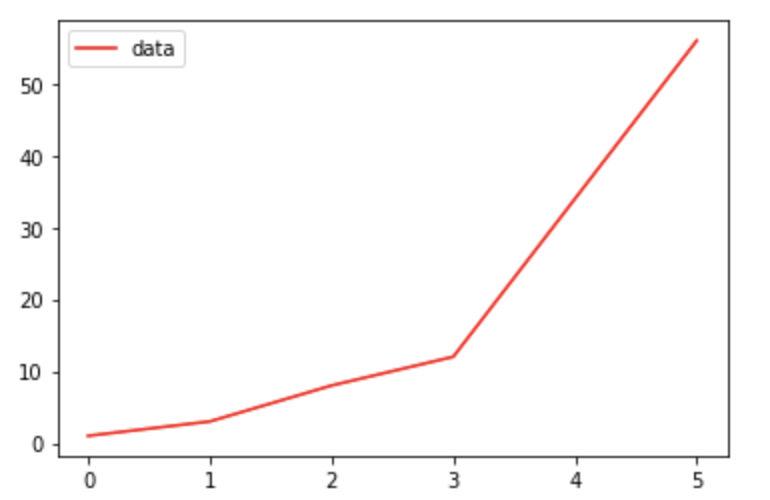
また、plot() 関数の引数を追加することで、グラフの線の色を変えたり、ラベルを加えたりできます。 以下では、legend() 関数を呼び出すことでグラフ内に凡例を表示しています。
# matplotlibのpyplotモジュールをpltという名前としてインポート import matplotlib.pyplot as plt # グラフを描画するためのデータを格納するリスト a = [1,3,8,12,34,56] # リストa内のデータを折れ線グラフとして描画 plt.plot(a, color="red", label="data") # 凡例の表示 plt.legend() # グラフの表示 plt.show()
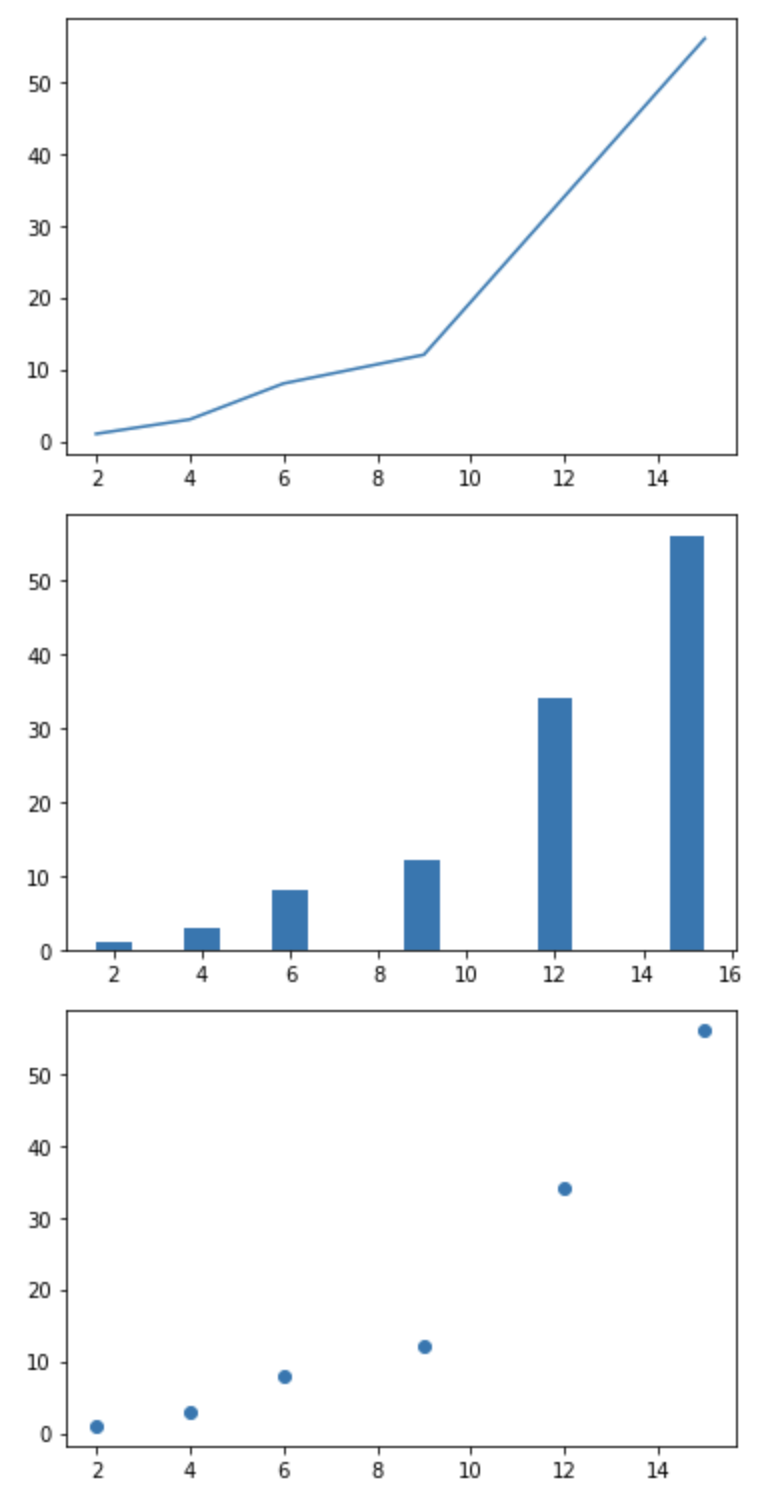
また、以下のように横軸のデータも用意すれば、折れ線グラフの他にも棒グラフや散布図も簡単に描けます。
# matplotlibのpyplotモジュールをpltという名前としてインポート import matplotlib.pyplot as plt # グラフを描画するためのデータを格納するリスト x = [2, 4, 6, 9, 12, 15] a = [1,3,8,12,34,56] # 折れ線グラフを描画 plt.plot(x,a) plt.show() # 棒グラフグラフを描画 plt.bar(x,a) plt.show() # 折れ線グラフを描画 plt.scatter(x,a) plt.show()
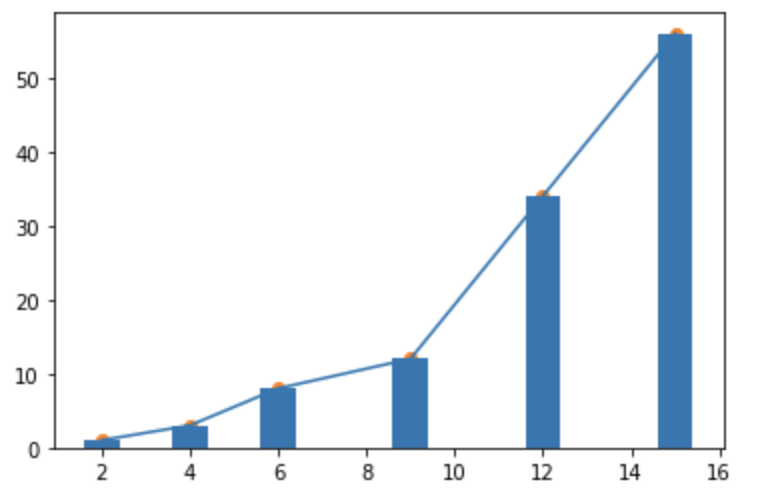
下のように plt.plot() を最後に1回だけ呼び出すと 同じ枠内にグラフを重ね書きすることに注意しましょう。
# matplotlibのpyplotモジュールをpltという名前としてインポート import matplotlib.pyplot as plt # グラフを描画するためのデータを格納するリスト x = [2, 4, 6, 9, 12, 15] a = [1,3,8,12,34,56] # 折れ線グラフを描画 plt.plot(x,a) # 棒グラフグラフを描画 plt.bar(x,a) # 折れ線グラフを描画 plt.scatter(x,a) # グラフの表示 plt.show()
複数のグラフを描画する際には、figure() 関数を用いてグラフの描画領域を作成した上で、 add_subplot() 関数で描画領域内での描画場所を指定します。
add_subplot(n, m, k) の3つの引数は、領域を n 行 m 列で分割した上で位置 k にグラフを配置する、
という意味です。
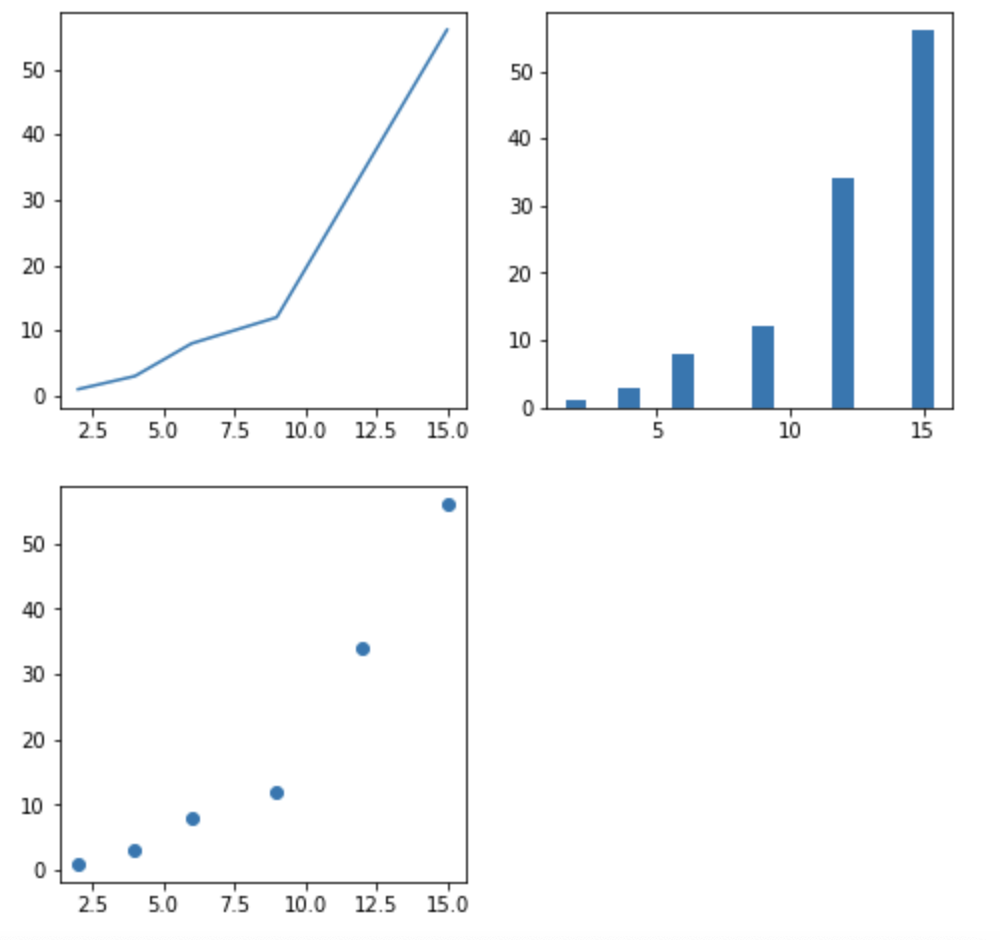
以下では、3つの異なる分割方法でグラフを配置しています。
# matplotlibのpyplotモジュールをpltという名前としてインポート import matplotlib.pyplot as plt # グラフを描画するためのデータを格納するリスト x = [2, 4, 6, 9, 12, 15] a = [1,3,8,12,34,56] # グラフの描画領域を作成 fig1 = plt.figure() # 描画領域内での描画場所を指定(3行1列で配置) ax11 = fig1.add_subplot(3,1,1) ax12 = fig1.add_subplot(3,1,2) ax13 = fig1.add_subplot(3,1,3) # 折れ線グラフを描画 ax11.plot(x,a) # 棒グラフグラフを描画 ax12.bar(x,a) # 折れ線グラフを描画 ax13.scatter(x,a) # グラフの描画領域を作成 fig2 = plt.figure() # 描画領域内での描画場所を指定(1行3列で配置) ax21 = fig2.add_subplot(1,3,1) ax22 = fig2.add_subplot(1,3,2) ax23 = fig2.add_subplot(1,3,3) # 折れ線グラフを描画 ax21.plot(x,a) # 棒グラフグラフを描画 ax22.bar(x,a) # 折れ線グラフを描画 ax23.scatter(x,a) # グラフの描画領域を作成 fig3 = plt.figure( figsize=[8,8] ) # 描画領域内での描画場所を指定(2行2列で配置) ax31 = fig3.add_subplot(2,2,1) ax32 = fig3.add_subplot(2,2,2) ax33 = fig3.add_subplot(2,2,3) # 折れ線グラフを描画 ax31.plot(x,a) # 棒グラフグラフを描画 ax32.bar(x,a) # 折れ線グラフを描画 ax33.scatter(x,a) # グラフの表示 plt.show()
描画領域の大きさを変更したい場合には、figure( figsize=[10,10] ) のように引数を設定すればOKです。

次に、第4回でも行なった sin 関数の描画を matplotlib を使って行なってみましょう。 (プログラミング演習 I でも行なっているようですが)
import numpy as np
import matplotlib.pyplot as plt
# 等差数列を生成する numpy の関数 linspace により、始点0, 終点20, 項数100の等差数列を生成
# つまり、0~20の区間内を等分割にして100個の点のリストを生成
x = np.linspace(0, 20, 100)
# sin(x)の値を格納したリストを生成(要素数は x と同じ100個)
y = np.sin(x)
# グラフの描画
plt.plot(x, y, label="sin(x)")
plt.title("Sine Curve : y = sin(x)")
plt.legend()
plt.show()
ここでは、数値計算用のパッケージである numpy を利用して等間隔のデータ列や sin 関数の計算を行なっています。
linspace() 関数による等間隔のデータ列(リスト)の作成は非常によく使いますので、ぜひ使えるようにしておいてください。
引数として値のリストを与えれば、計算によって返ってくる値もリストになっているため、
C 言語の時のように明示的に for 文による繰り返し処理をプログラムで書く必要がありません。
これにより、Python ではこのようなグラフの描画も非常にシンプルなプログラムで書くことができます。

ヒント
グラフを描いた枠を横並びに表示するには、上で説明したようにfigure()で描画領域を作成した上で、 add_subplot()で描画場所を指定する。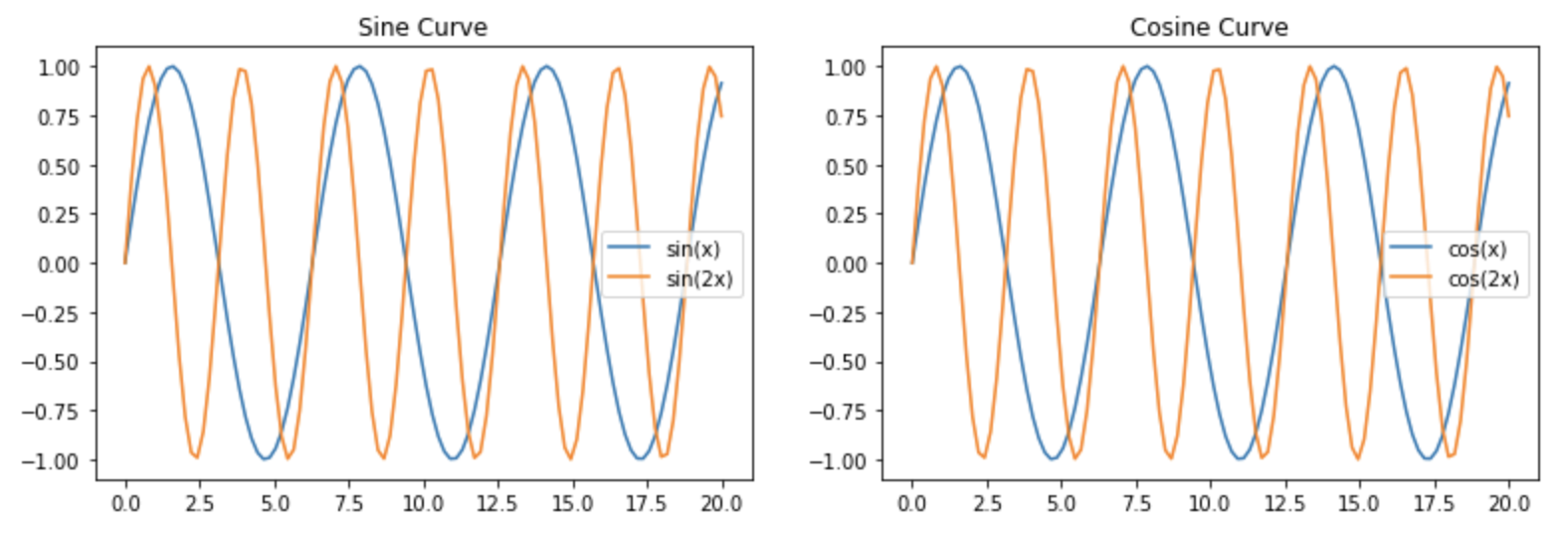
グラフのアニメーションに関しても、第4回でも行なった C 言語によるアニメーションと基本的な考え方は同じです。
matplotlib を利用したアニメーションの作成方法はいくつかありますが、今回はArtist Animation を用いた方法を紹介します。
Google Colaboratory上でのアニメーションは、通常の Jupyter Notebook 上でのアニメーション作成方法と少し異なる箇所があります。 この授業でのプログラムを通常のJupyter Notebook 上で実行しても同じ挙動を示すとは限らないことに注意して下さい。
ArtistAnimationを用いたアニメーションでは、アニメーションの各コマで用いる少しずつずらしたグラフをあらかじめ用意してから、
それらを結合させてアニメーションとして表示します。
あらかじめグラフを全て用意しなければいけないため、アニメーションのコマ数が多い場合には描画までに時間がかかります。
そのような場合には、FuncAnimation を利用した方法でアニメーションを行う方が一般的です。
FuncAnimation の使い方については、次回以降に紹介する予定です。
import numpy as np
import matplotlib.pyplot as plt
from matplotlib import animation, rc
from IPython.display import HTML
# 0~4πの区間内を等分割にして100個の点のリストを生成
x = np.linspace(0, 4*np.pi, 100)
# グラフの描画領域を作成
fig = plt.figure(figsize=[8,4])
# 描画領域内での描画場所を指定(1行1列で配置)
ax = fig.add_subplot(1,1,1)
# 各コマのグラフを格納するために、空のリスト作成
ims=[]
# 描画の終了時間
T = 10
# 描画の1stepの時間
dt = 0.5
# 現在の時間
t = 0
# 凡例を1回だけ表示させるためのフラグ
f_legend = True
# 時刻 T までループ
while t <= T:
# 現在の y の計算
y = np.sin(x + t)
# 現在のグラフを描画
im = ax.plot(x, y, color='red',label="sin(x+t)")
# グラフをリストに追加
ims.append(im)
# 時間を進める
t += dt
# 一度だけ凡例を表示
if f_legend:
ax.legend()
f_legend = False
# 各軸のラベル
ax.set_xlabel("x", fontsize=15)
ax.set_ylabel("y", fontsize=15)
# グラフの範囲を設定
ax.set_xlim([0, 4*np.pi])
ax.set_ylim([-1.1, 1.1])
# ArtistAnimationにfigオブジェクトとimsを代入してアニメーションを作成
anim = animation.ArtistAnimation(fig, ims)
# Notebook 上で表示するためのおまじない
plt.close()
HTML(anim.to_jshtml())
今までに出てこなかった関数も出てきますが、基本的な考え方はシンプルです。
while による繰り返し処理のループ内で、時間を少しずつずらしたグラフを作成(im = ax.plot()の箇所)し、
それを ims というリストに追加しています(ims.append(im)の箇所)。
また、各stepごとに dt だけ時間を追加しています。
凡例については、毎回表示させるとコマ数分だけずれた位置に表示されてしまうため、
ループ内で一度だけ表示するようにしています。
ループが終わったら、最後に fig オブジェクトと ims オブジェクトをArtistAnimationに引数として渡して、
アニメーションを作成します。
最後の行は、Notebook 上で表示するためのおまじないです。
ヒント
グラフを描いた枠を縦並びに表示するには、上で説明したようにfigure()で描画領域を作成した上で、 add_subplot()で描画場所を指定する。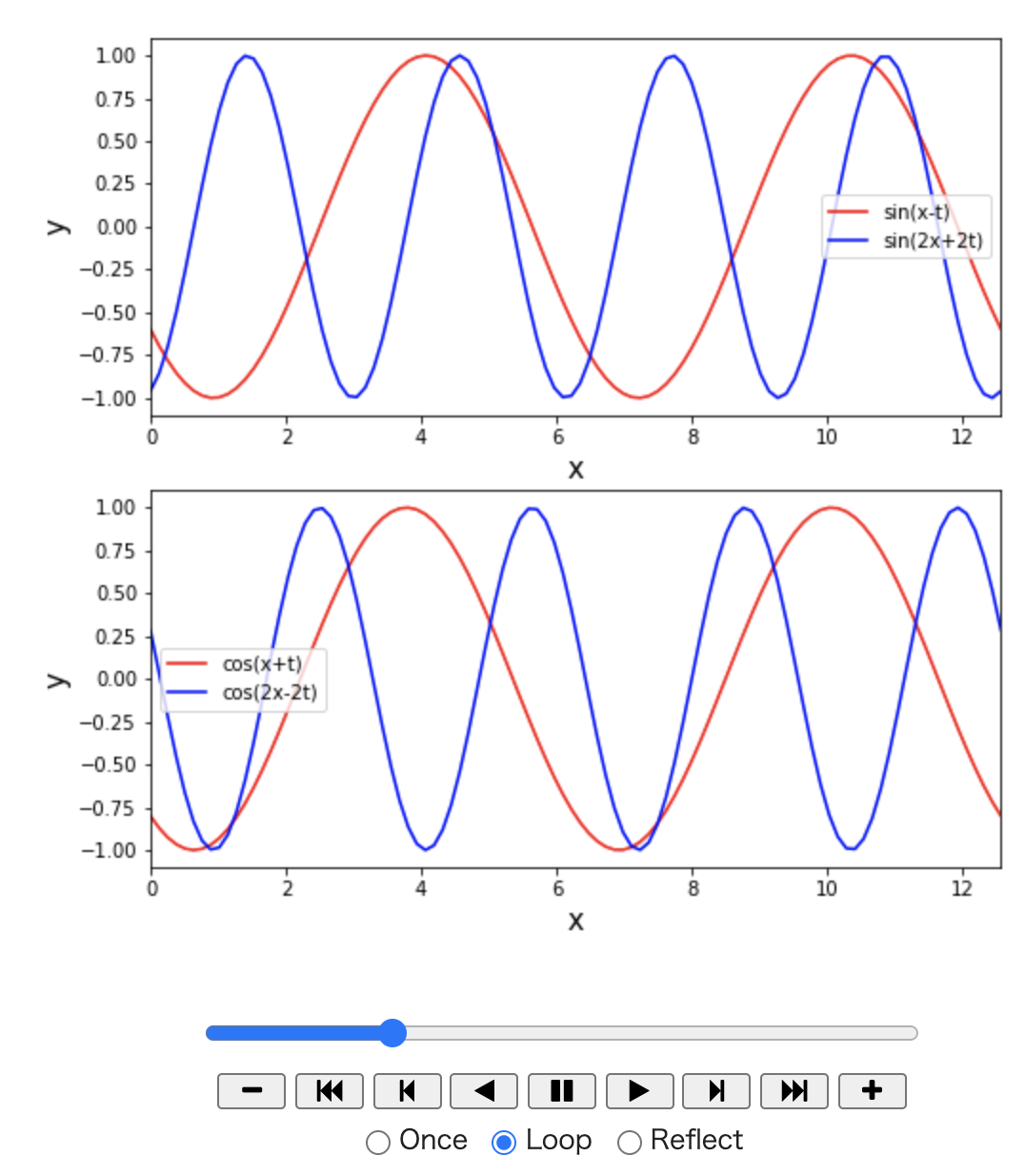
「課題1」と「課題2」の両方について作成したプログラムを提出してください。 課題1と課題2は一つのファイルに入れてしまって構いません。
ただし、コメント文として
学生番号、名前、プログラムの簡単な説明
を書く事。
ファイル名は、08-rep.ipynb として、 提出したファイル単体で実行できるようにすること。
提出締め切り: 2024年11月25日19時