第２回　簡単な数値計算とgnuplotを用いた可視化、C言語のおさらい２（関数、ポインタ）　(2024年9月30日)

今日の内容

前回の課題1および課題2-(2)について

前回の課題1について

前回の課題1の小問2,3に関して、 毎年変数の型について理解がきちんとできていない人が少なからず見受けられるので、 今一度おさらいしておきましょう。 

int a = 1;
int b = 2;

printf("%d\n", a/b);

このように書くと、小問1にもあるとおり、0が表示されます。
これはもちろん a / b が整数同士の演算になっているからです。
整数同士の演算の結果は、当然整数なので 1 / 2 = 0.5 とはならず、0.5が切り捨てられた 0 が演算の結果となります。

これを次のように書き換えてみましょう。 

double a = 1;
int b = 2;

printf("%lf\n", a/b);

すると今度はきちんと0.5が表示されます。
これは a を実数型にしたことによって、a / b の演算結果が自動的に実数型に変換されるためです。
このような自動的な型変換のことを暗黙的型変換と呼びます。
他にも、実数型変数に整数型変数を代入しようとした場合に、右辺の整数型が自動的に実数型に変換されて左辺の実数型変数に代入される場合にも、 暗黙的型変換が起こっています。

それでは次のように書き換えた場合はどうなるでしょうか？ 

int a = 1;
int b = 2;
double c = a/b;

printf("%lf\n", c);

今度もきちんと 0.5 が表示されると思いきや、0.0が表示されます。
これは、c が実数型だとしても a / b の演算結果はあくまで整数型なので、切り捨てられた 0 が右辺の結果となります。
これが左辺に代入されてしまうので、実数型への暗黙的型変換が起こっても 0 が表示されるのです。

これを防ぐためには、以下のように書く必要があります。 

int a = 1;
int b = 2;
double c = (double)a/b;

printf("%lf\n", c);

すると今度は0.5が表示されます。
演算 a / b の前にある(double)は明示的型変換（キャスト）と呼ばれるもので、 一時的に変数の型を変換させることができます。
ここでは、int 型変数 a を一時的に double 型変数に変換することで右側の演算が double / int になるので、 右辺の演算結果が 0.5 となり、これがそのまま左辺に代入されます。
整数同士の演算の結果は、当然整数なので 1 / 2 = 0.5 とはならず、0.5が切り捨てられた 0 が演算の結果となります。

上記のような型変換にまつわる間違いは、今後の課題でも毎年かなり多く発生するので、 今回間違えなかった人も含めてよく注意しましょう。

前回の課題2-(2)について

前回の課題2-(2)の解答例は、こちら

乱数の発生回数を増やすと、円周率の近似値が正確な値に近づくのは簡単に予想できたと思いますが、 円の場合と球の場合の違いはきちんと理解できたでしょうか。

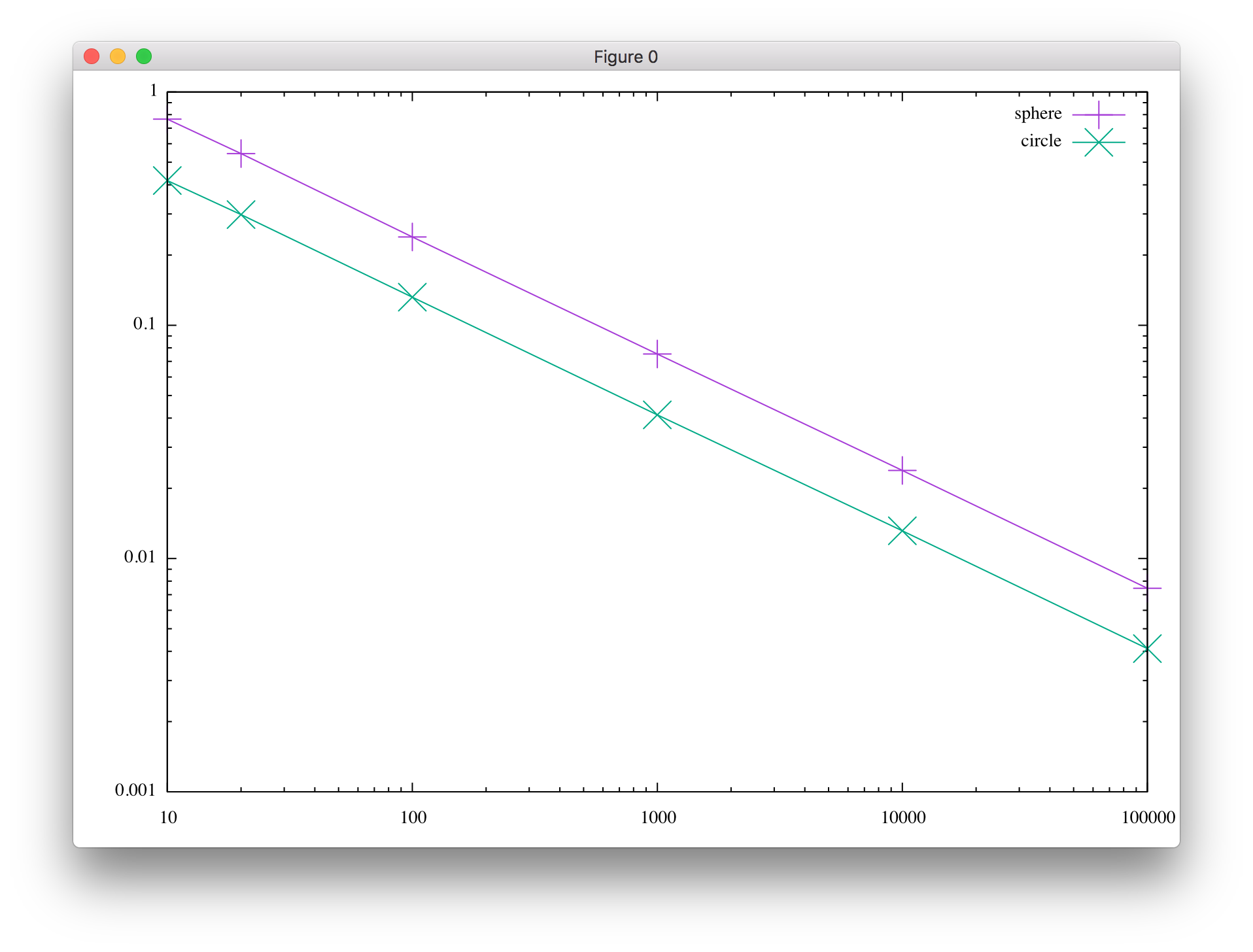
下の図は、横軸が乱数を発生させた回数（サンプル数）、 縦軸は求めた円周率の正確な値からのずれの絶対値（10000回の試行の平均値、誤差）を表しています。 乱数の発生回数が増えると正確な値からのずれが小さくなること、および球（sphere）よりも円（circle）の場合の方が ずれが小さいことがわかります。

ただし、サンプル数を大きくしていったときの誤差の変化（グラフの傾き）は球と円で同じになっています。 これは非常に重要な性質で、高次元の数値積分を行う際に大きな威力を発揮します。 通常の数値積分法では次元が上がるほど精度を上げるために必要な計算量が指数的に増加する（次元の呪い）のに対し、 乱数を用いた数値積分（モンテカルロ積分）では次元に依存しないため、 高次元の数値積分を効率的に行うことが可能となります。

gnuplot および GLSC3D 利用の準備

2024年度も引き続き、GLSC3D を利用します。

今回利用するgnuplotおよび次回から利用するGLSC3Dの下準備を行います。 この準備ができていないと今回以降の演習ができませんので、本日の演習で確実に準備を行います。

2024年度入学の学生以外は以前の授業で gnuplot および GLSC3D が使える状態のはずなので、 以下では2024年度入学の学生向けに導入方法を説明していきます。


gnuplot利用のための準備

gnuplot を利用可能な状態にする（パスを通す）作業を行います。
まず、以下の2つのファイルをダウンロードしてください。

test2024.sh

shexe2024.sh

次に、自分のホームディレクトリ(ev24xxxx)にダウンロードした2つのファイルを移動させてください。

続いてターミナルを開いて、以下のコマンドを１行ずつ実行してください。

cd

chmod u+x shexe2024.sh

./shexe2024.sh

source .zprofile

とします。 これらの作業の途中でエラーが出てしまった場合は、教員が対応しますので質問してください。

この作業で上手くいかない場合には、Macにログインしているアカウントに問題がある可能性があります。 自分で作成したアカウントにログインしている場合には一度ログアウトして、 入学時に最初から存在したアカウント（おそらく sougousuuri という名前）でログインしてみてください。

上記の作業がうまくいけば、前回起動できなかった gnuplot が起動できるはずです。

二分法

非線形方程式の根を求めることは、応用上とても重要です（世の中の現象の多くは、非線形な方程式で表される）。 ここでは、二分法によって根を求めるプログラムを実際に作成し、アルゴリズムとプログラムとの対応をみましょう。

次の問題を考えてみましょう。

もちろん答えは x = √2 ですが、それを二分法を用いて近似的に求めましょう。 （無理数である√2 を近似的に求めるアルゴリズムともいえます。）

gnuplot を用いた二分法の直感的な理解

二分法は、求めたい根を２つの値で挟み込み、徐々に幅をせばめていくことで根を求めるアルゴリズムですが、 根を挟み込む値はこちらが前もって与える必要があります。 今回の例については簡単にグラフを書くことができますが、そうでないこともありますし、 関数のグラフを簡単に確かめたいこともあるでしょう。 そういう場合には、gnuplot を用いてグラフを描画することで、視覚的に理解することができます。

ターミナルで、

gnuplot

と打ち込み、改行キーを押すことで gnuplot が起動します。 起動すると、ターミナル上のプロンプトは gnuplot のものとなり、 gnuplot のコマンドを入力できる状態となります。そこで、

plot　x*x - 2

とすることで、y = x2 - 2 のグラフが得られます。 x の範囲は自動的に決まりますが、以下のように自分で設定することもできます。
例えば、0 ≦ x ≦ 2の区間でグラフを表示したい場合には、以下のようにします。

plot　[0:2]　x**2 - 2

ちなみに、x2は x**2 と表記できます（xnなら x**n）。 同時に f(x) = 0 のグラフも描くとわかりやすいので、書き加えます。

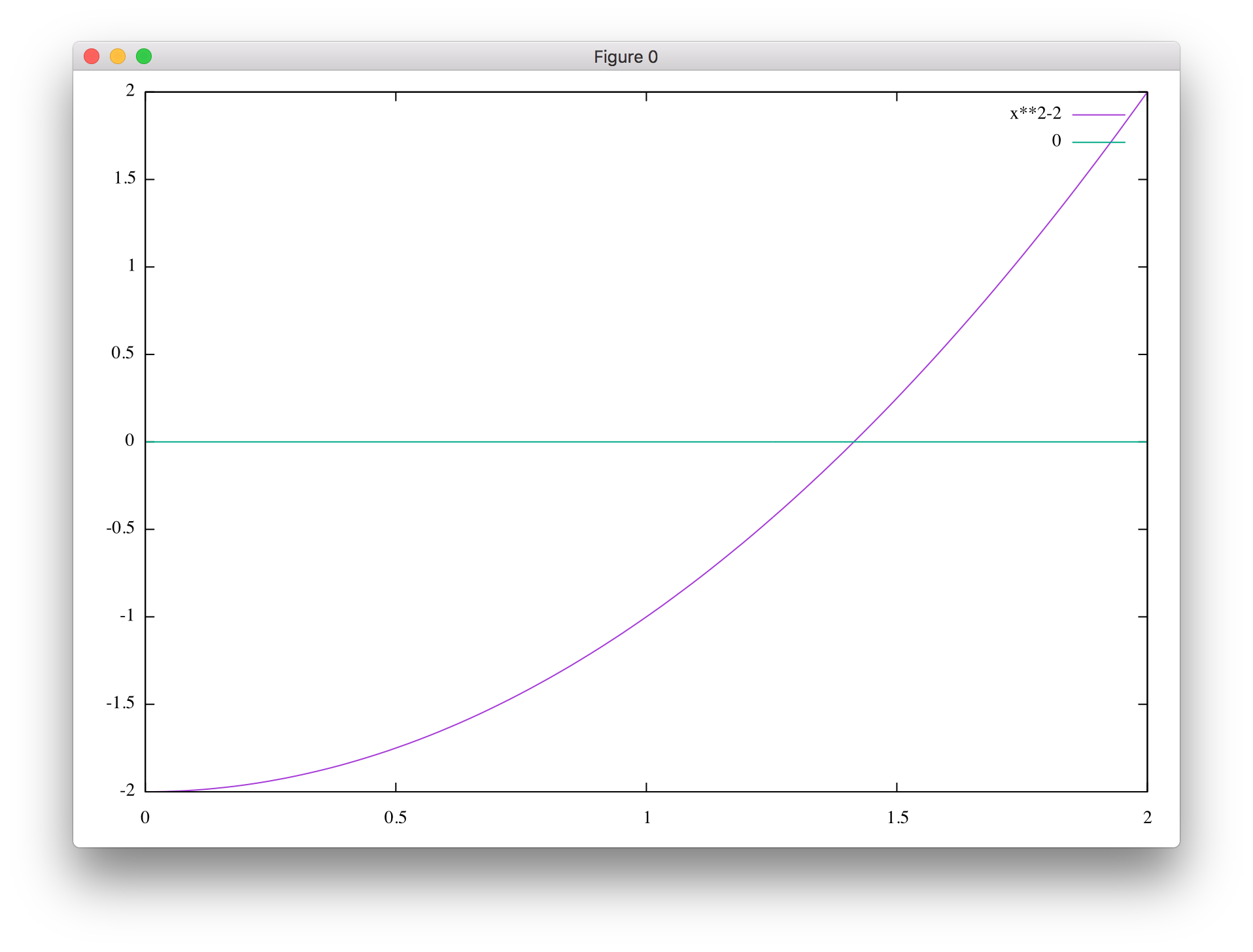
plot　[0:2]　x**2 - 2, 0

すると、下図のような結果が得られ、求めたい根は 1 と 2 の間にあることがわかります。

gnuplot は、

quit

で終了できます。

たとえば、次のようなものも試してみてください。

plot　sin(x)

plot　x**3 - x**2 + 5

C言語による二分法の実装例

まず、二分法のアルゴリズムを示します。

二分法のアルゴリズム

上記アルゴリズムをC言語のプログラムとして実装した例を示します。 ここでは、fabs 関数、exit 関数と、break 文を使っています。

fabs 関数は、引数として実数値をとり、戻り値としてその絶対値を返します。

exit 関数は、引数として整数値をとり（与える整数値には意味はあるが、当面何でも良い）、プログラムを終了させます。 ここでは、A, B の値が不適切であれば、メッセージを表示して終了するようにしています。

break 文は、繰り返し文から強制的に抜ける場合に用います。 ここでは fc == 0.0 という起こりそうに無い状況が起きた場合に使っています。

なお、このプログラムでは数学関数である fabs 関数を使っているので、 コンパイル方法がこれまでと少し異なります。 以下のプログラムをたとえば Bisec.c として打ち込んだ場合、コンパイルは以下のようにします。

cc　Bisec.c　-o　Bisec　-lm

最後の -lm が変更点で（マイナス・小文字のエル・小文字のエム）、数学関数は標準関数では無いため、 このような指定が必要です。 不正確な説明ですが、数学関数を使うので、その数学関数集として定義されたものを自前のプログラムに ひっつける（リンクさせる）ということです。 例えば、sin 関数等も数学関数として使うことができますが、その場合にも同様に -lm が必要になります （コンパイラによっては、sin 関数などを利用する場合は必要ない場合もある）。

以下が、C言語によるソースコードです。

// 二分法
#include <stdio.h>
#include <stdlib.h> // exit 関数を用いる為に必要
#include <math.h>   // fabs 関数を用いる為に必要


double  f(double x);      // 関数 f(x) のプロトタイプ宣言


#define A (1.0)           // f(A) < 0 となるような A を設定
#define B (2.0)           // f(B) > 0 となるような B を設定
#define E (1.0e-10)       // 収束判定に用いる

int main()
{
    // 使用する変数の宣言
    double a, b, c, e, fc;
    int i;

    // 変数の初期化
    i = 0;
    a = A;
    b = B;
    e = E;

    // A, B の値の妥当性チェック
    if( !( (f(a) < 0) && (f(b) > 0) ) )
    {
        printf("A, B の値が不適切です。\n");
        // プログラムを終了させる標準関数
        exit(0);
    }

    // 二分法アルゴリズム
    // |a-b| / 2 > e の間繰り返す
    while( fabs(a - b) / 2.0 > e )
    {
        c = (a + b) / 2.0;

        fc = f(c);

        i++;

        // 繰り返しの回数 i と c の値を表示
        // %10.8lf とは、全部で10文字、小数点以下8桁で表示するという意味
        printf("%d %10.8lf\n", i, c);

        // c の符号により a または b に c を代入
        if( fc > 0.0 )
        {
            b = c;
        }
        else if( fc < 0.0 )
        {
            a = c;
        }
        // fc == 0.0 であれば、c は根であるから繰り返し文を強制的に抜ける
        else
        {
            // break 文によって強制的に繰り返し文を抜けることができる
            break;
        }
    }
}

// 関数 f(x) の定義
double f( double x )
{
    return (x*x - 2.0);
}

上記のサンプルプログラムでは、繰り返しごとに繰り返し回数 i とそのときの c の値を表示するようにしてあります。 このプログラムを実行すると、数値の列が表示されます。

ターミナルで、以下のようにコンパイルして実行します。
（ちなみに、ccg Bisec.c でコンパイルしても下のコンパイルと同様に、Bisec という実行ファイルが生成されます）

cc Bisec.c -o Bisec -lm

./Bisec

実行すると、数値の列がみられ、繰り返しごとに√2の値に近づく様子がわかります。 この数値の列を gnuplot でグラフとしてみるには、次のようにします。

./Bisec > sqrt2.data

このようにすることで、画面には表示されず、sqrt2.data というファイル名のファイルに書き込まれます。 たとえばエディターで sqrt2.data というファイルを開いてみればわかります。 さて、gnuplot で ファイル内の数値を可視化しましょう。

ターミナルで、

gnuplot

として gnuplot を起動し、

plot "sqrt2.data" with linespoints, sqrt(2)

とすると、次のようなグラフが得られます。

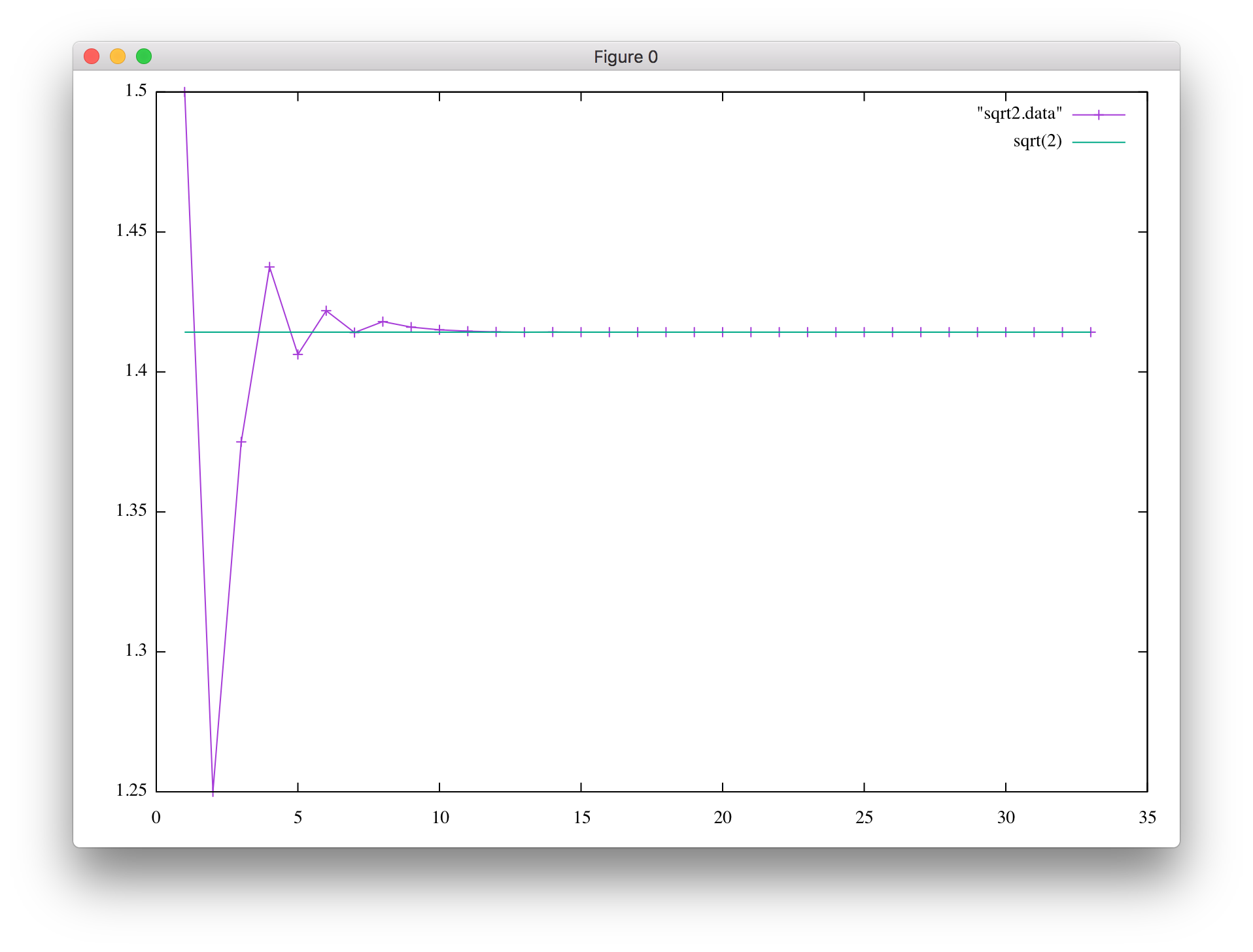
> などの記号を使ってファイル等に出力することをリダイレクトと呼びます。 ちなみに、「コマンド > hoge」の場合にはコマンドによる出力を hoge というファイルに 上書き（既存の情報は全て破棄）するのに対し、「コマンド >> hoge」の場合には コマンドによる出力を hoge というファイルの最後尾に追加書き込み（既存の情報は保持）します。 必要なファイルの情報を消してしまわない様に注意して使いましょう。

データの書き出しと入力促進メッセージに関する重要な注意

上記のように、計算結果を printf 文で数値を画面に表示した後に、gnuplot でそれらをグラフ化する場合、 入力促進メッセージの表示方法が問題となります。 （上記の例には scanf による入力がありませんが、例えば変数 a,b,e をそれぞれ入力し、 実行するようなプログラムが考えられ、その場合には入力促進メッセージが必要となるだろう。）

すなわち、プログラム名が prog であるときに、

./prog > some.data

として、printf 関数の出力を画面ではなく some.data に書き込むわけですが、 このままでは入力促進メッセージ(「初期値を入力してください」といったメッセージ)も画面に表示されず、 some.dataに書き込まれてしまいます。 これではメッセージの意味がない上に、不要な文字列が some.data に書き込まれ、 gnuplot でグラフを作成する際に問題となります。

そこで、入力促進メッセージに関しては通常の printf 関数は使わず、 fprintf 関数を用いることで上記の問題に対応します。 具体的には、入力促進メッセージについては、例えば、

fprintf(stderr, "a の値を入力してください");

というように、

fprintf(stderr, "文字列");

を用いてください。 "文字列" の部分は通常の printf 文と同様に使うことができ、変数内の数値の表示などに使う %d 等の変換文字列も同様に使えます。stderr は文字列の表示先を「標準エラー出力」にせよという意味です。 実は、通常の printf 文は、

fprintf(stdout, "文字列");

と同等です。stdout は「標準出力」と呼ばれ、通常これはターミナルの画面です。 「標準エラー出力」も通常ターミナル出力ですが、プログラムを以下のように実行した際には

./prog > some.data

「標準出力」の出力が some.data に書き込まれ「標準エラー出力」の出力は画面に表示されることになります。

以上をまとめると、以下のようになります。

データの書き出しについては、上記の方法の他にも fopen 関数、fclose 関数等のファイル入出力関数を用いる方法もあります。 様々な参考書やネット上での情報がありますので、自分で勉強してみてください。

gnuplot を用いたグラフ画像の作成

上記で作成したようなグラフを画像ファイルとして保存し、レポートに貼り付けたりすることもあるでしょう。 そのような場合には、先ほどのグラフの描画命令に続いて、次のように入力します。

set term png
set output "graph.png"
replot
quit

これで graph.png という画像ファイルが作成されます。 例えば、sin(x) のグラフの png ファイルを作りたい場合には、gnuplot を起動後、次のようにします。

set term png
set output "sin_graph.png"
set title "Graph of sin(x)"
set xlabel "x"
set ylabel "sin(x)"
plot sin(x)
quit

title や plot の部分は適宜変更します。 png 部分（2カ所）を jpg に変更すれば jpeg 形式で保存されます。 詳しくは、gnuplot を起動して、

set　term

と打ち込むと出力ファイル形式の一覧が得られますので、それを参考にしてください。

gnuplotの使い方 その2

二分法において、c の値が繰り返し毎にどのように変化するかを確認しました。 このとき、他の a, b の値はどのように変化するでしょうか？ すべての値の変化を、まとめてグラフでみることはできないでしょうか？ そのために、上記のプログラムを以下のように少々変更します。 変更部分は赤字部分です。 このプログラムを、Bisec-2.c としましょう。

// 二分法
#include <stdio.h>
#include <stdlib.h> // exit 関数を用いる為に必要
#include <math.h>   // fabs 関数を用いる為に必要


double  f(double x);      // 関数 f(x) のプロトタイプ宣言


#define A (1.0)           // f(A) < 0 となるような A を設定
#define B (2.0)           // f(B) > 0 となるような B を設定
#define E (1.0e-10)       // 収束判定に用いる

int main()
{
    // 使用する変数の宣言
    double a, b, c, e, fc;
    int i;

    // 変数の初期化
    i = 0;
    a = A;
    b = B;
    e = E;

    // A, B の値の妥当性チェック
    if( !( (f(a) < 0) && (f(b) > 0) ) )
    {
        printf("A, B の値が不適切です。\n");
        // プログラムを終了させる標準関数
        exit(0);
    }

    // 二分法アルゴリズム
    // |a-b| / 2 > e の間繰り返す
    while( fabs(a - b) / 2.0 > e )
    {
        c = (a + b) / 2.0;

        fc = f(c);

        i++;

        // 繰り返しの回数 i と a, b, c の値を表示
        // %10.8lf とは、全部で10文字、小数点以下8桁で表示するという意味
        printf("%d %10.8lf %10.8lf %10.8lf\n", i, a, b, c);

        // c の符号により a または b に c を代入
        if( fc > 0.0 )
        {
            b = c;
        }
        else if( fc < 0.0 )
        {
            a = c;
        }
        // fc == 0.0 であれば、c は根であるから繰り返し文を強制的に抜ける
        else
        {
            // break 文によって強制的に繰り返し文を抜けることができる
            break;
        }
    }
}

// 関数 f(x) の定義
double f( double x )
{
    return (x*x - 2.0);
}

プログラムを保存したら、次にターミナルでコンパイルして、実行してみましょう。

cc Bisec-2.c -o Bisec-2 -lm

./Bisec-2

上記のようにすることで、数値の列がみられます。 最初の例では2列のデータでしたが、今度は4列のデータが得られます。 プログラムを見ればわかりますが、1列目から順に、繰り返し数 i、a の値、bの値、cの値となっています。 そこで次に、先ほどと同様にファイルにデータを書き出してみましょう。

./Bisec-2 > sqrt2.data3

今度は、sqrt2.data3 というファイルにデータが書き込まれます。 では次に、gnuplot で ファイル内の数値を可視化してみましょう。

ターミナルで、

gnuplot

として gnuplot を起動し、先程と同様に入力してみましょう。

plot "sqrt2.data3" with linespoints, sqrt(2)

すると、期待に反して先とほぼ同様の結果が得られます。 gnuplot は何も指示しなければ、横軸に1列目の値を用い、縦軸に2列目の値を用います。 同時に a, b, c の時間変化をみたい場合には、次のように指定する必要があります。 gnuplot に、続けて以下のように打ち込んでみましょう。

plot "sqrt2.data3" using 1:2 with linespoints, "sqrt2.data3" using 1:3 with linespoints, "sqrt2.data3" using 1:4 with linespoints

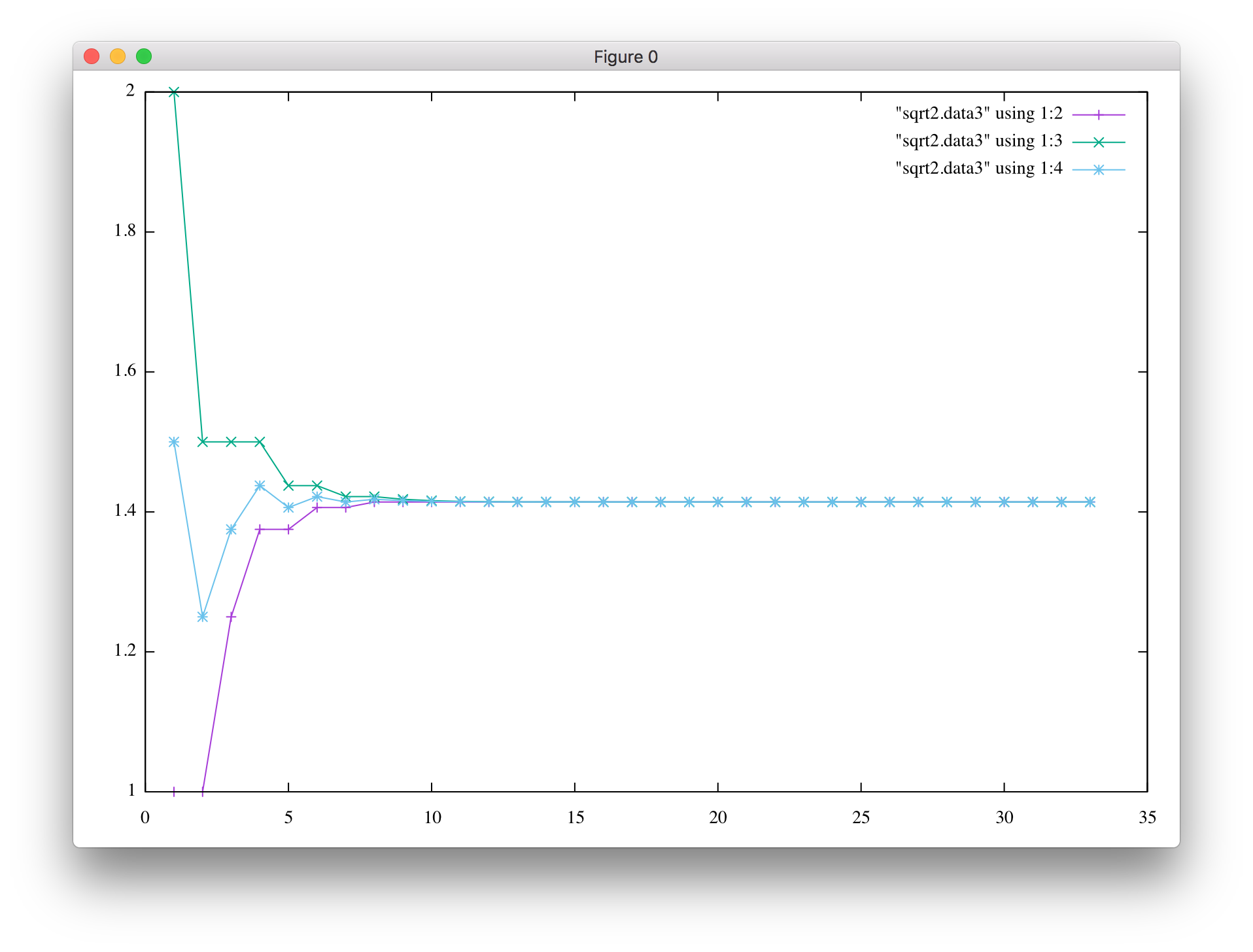
"using x:y" という指定によって、どの列を「横軸:縦軸」に使うかを指示できます。 上のグラフを見ると、c（青) は a（赤）と b（緑）の中点になっていることがわかります。 グラフの見栄えをもう少しよくしてみましょう。 ちなみに、with linespoints は w lp と省略できます。 一番下の t "a" などは、title "a" の省略です。

set title "Graph"
set xlabel "i"
set ylabel "a,b,c"
plot "sqrt2.data3" using 1:2 w lp t "a", "sqrt2.data3" using 1:3 w lp t "b", "sqrt2.data3" using 1:4 w lp t "c"

Mac における画面のスクリーンショットの撮り方

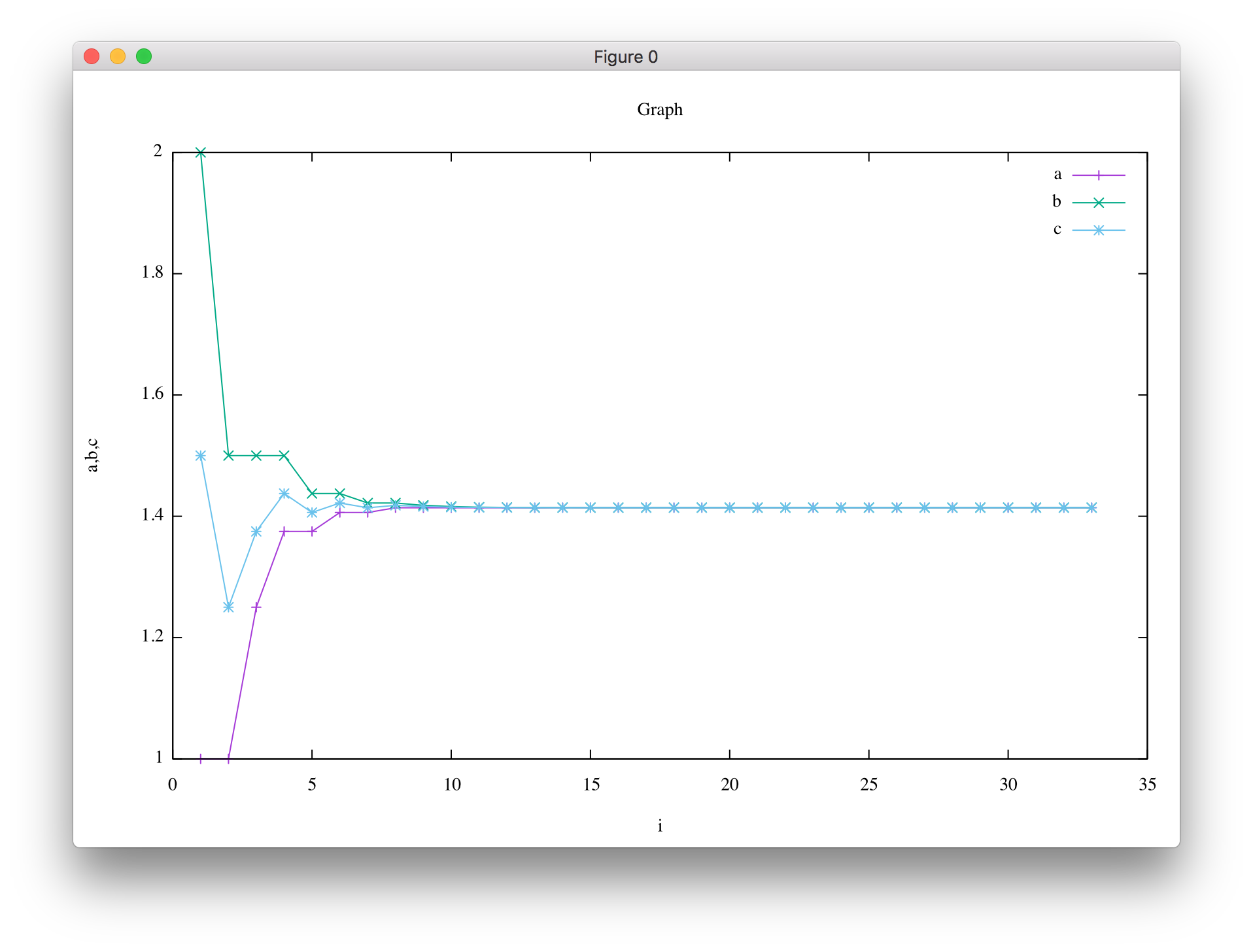
詳しくは、こちらを参照してください。

画面全体のスクリーンショットで必要ない部分を切り取るのが面倒な場合には、 ウィンドウのスクリーンショットを撮る（「command + shift + 4」の後、スペースを押し、撮りたいウィンドウをクリック） のが便利です。

関数の定義と利用

これまで、標準関数と呼ばれる関数をいくつか使いました( printf 関数と scanf 関数）が、 C言語では自分で関数を定義できます。

C言語ではこれから述べる関数のプロトタイプ宣言を書くことが一般的です。 これはプログラムエラーを減らす為の仕組みですので、ぜひ活用しましょう。

 1: #include <stdio.h>
 2: 
 3: int beki(int a, int b);
 4:
 5: int main()
 6: {
 7:     int n;
 8:
 9:     n = beki(2, 3);
10:     printf("%d\n", n);
11:
12:     printf("%d\n", beki(3, 4));
13:
14:     return 0;
15: }
16:
17: int beki(int a, int b)
18: {
19:     int i, ans;
20:
21:     ans = 1;
22:
23:     for (i = 1; i <= b; i++)
24:     {
25:         ans = ans*a;
26:     }
27:  
28:     return ans;
29: }

緑字の部分（３行目および１７〜２９行目）が関数の定義に関わる部分で、 赤字の部分（９行目および１２行目）が定義した関数を使用している部分です。 まずは定義している部分から見ていきましょう。

３行目：

関数のプロトタイプ宣言と呼ばれる宣言です。 後に定義する関数の戻り値の型と引数の型を仕様として、プログラムの先頭部分（main 関数より前）にこのように書きます。 関数を定義する場合には、このプロトタイプ宣言が必ず必要だと思っておいてください。 （省略する方法もありますが、この演習では必ずプロトタイプ宣言をすることとします。）

５〜１５行目：

　main 関数の定義です。

１７〜２９行目：

　beki 関数の定義です。

戻り値と引数

y = sin(x)

と書いたとき、sin が関数名で x が関数 sin の引数。 変数 y には sin(x) の戻り値が入ることになります。 当然変数 x, y にはそれぞれ型があり、関数自体がもつ値（戻り値）にも型があります。

　先のサンプルプログラムの３行目のプロトタイプ宣言や、１７行目の関数定義の部分で、 int と整数型が宣言されているのはその為です。

beki 関数の定義

　では、beki 関数の定義部分を詳しく見てみましょう。１７行目を見ると、

int beki (int a, int b)

となっています。 これは、先のプロトタイプ宣言と通常おなじ記述となります。 はじめの int は、beki 関数の戻り値の型が int であるという意味です。 続いて関数名 beki があり、その後括弧に囲まれ、２つの変数が定義されています。 これらは、引数として渡される値を格納する為の変数で、 それらの名前をそれぞれ a, b とし、型はそれぞれ整数型としています。 つまり、beki(1,2) とこの関数が呼ばれた場合、 a には 1 が、 b には 2 が代入されることになります。

　続いて、中括弧に囲まれた、関数本体の処理内容が続きます。 この中で、新たに（この関数の定義内でのみ有効な）変数 i と ans を定義しています。 さらに23, 25行目では、先の引数部分にあった、変数 a, b が参照されています。 もちろん、 a, b には関数が呼ばれた時に引数として渡されている変数の中身の数値、 または直接数値として渡された場合にはその数値が代入されています。 重要な点として、変数自体が渡されているのではないので、 仮に関数内で a, b に別の値を代入しても、関数呼び出し側での変数（引数）の値が変更されないことに注意して下さい。 引数として渡す変数を関数内で変更したい場合には、このあと復習するポインタを利用します。

　最後の return 文により、 ans の内容が beki 関数の戻り値として返されます。

以上、関数を作る場合に必要なことをまとめると、以下の様になります。

プロトタイプ宣言の効用を見るために、 beki 関数において引数を一つだけにしてみましょう。 警告がでるはずです。

ポインタの基本

ポインタの概念は、わかってしまえば簡単ですが、記法が特殊で混乱しやすいため、説明を注意して聞いて下さい。 幾つか本を読んでもどうもよくわからないという人や、何となくわかったつもりで使っている人も良くいますが、 ここである程度しっかり理解しておきましょう。

これまで関数の利用において、複数の入力に対して、戻り値は一つの場合のみ扱ってきました。 場合によっては、複数の戻り値を得たい場合もあるでしょう。 C言語の特徴でもあるポインタを使えば、そのような事が可能になります。 （ポインタの概念は便利ですが、間違った使い方をすると、たちの悪いプログラムになりますから注意して使いましょう。 特に、配列を使う場合にはポインタの概念を良く理解する事が必要になります。）

例えば、二つの数値を与えると、それら数値の単純和・絶対値和・積の三つの計算をして答えを返す関数を作るとします。 これまでの知識ではうまく行きません。 例えば、以下の様なプログラムでうまく行きそうですが、実際にはうまく行かない事を確認してみましょう。 

#include <stdio.h>
#include <stdlib.h>
void calc01(int a, int b, int plus, int absplus, int mult);
int main()
{
  int a, b, c;
  a = 0; b = 0; c = 0;
  calc01(10, -10, a, b, c);
  printf("%d %d %d\n", a, b, c);
  return 0;
}
void calc01(int a, int b, int plus, int absplus, int mult)
{
  plus = a + b;
  absplus = abs(a) + abs(b);
  mult = a*b;
}

幾つか注意点があります。 まず、絶対値を求める標準関数 abs を使うため、 #include <stdlib.h> が記述されています。 また、calc01 関数について void とありますが、これは（関数としての）戻り値無しという意味です。 （関数 calc01 の定義内に return 文がありません。関数の途中で戻りたい場合には、その場所で return; と書く必要があります。）

main 関数内で整数型変数 a, b, c を用意し、それを関数 calc01 に渡し、関数内で計算内容を代入を代入しているので、 結果が表示されそうですがうまく行きません。

これまでにも学習した通り、C言語において上記の様な関数の記述では、関数の対応する変数に対して「値」が渡されます。 つまり、 main 関数内での calc01 の呼び出しでは、

calc01(10, -10, a, b, c);

となっていますが、a, b, c それぞれの変数の中に格納されている値が calc01 の定義にあるそれぞれ plus, absplus, mult に代入されます （今回の場合には、0, 0, 0 という数字が関数に渡されるだけ）。 main 関数内の a, b, c と calc01 内の plus, absplus, mult は別のもの（別の箱）ですから、 calc01 内の plus, absplus, multに計算結果を代入しても main 関数内の a, b, c に値は代入されません。

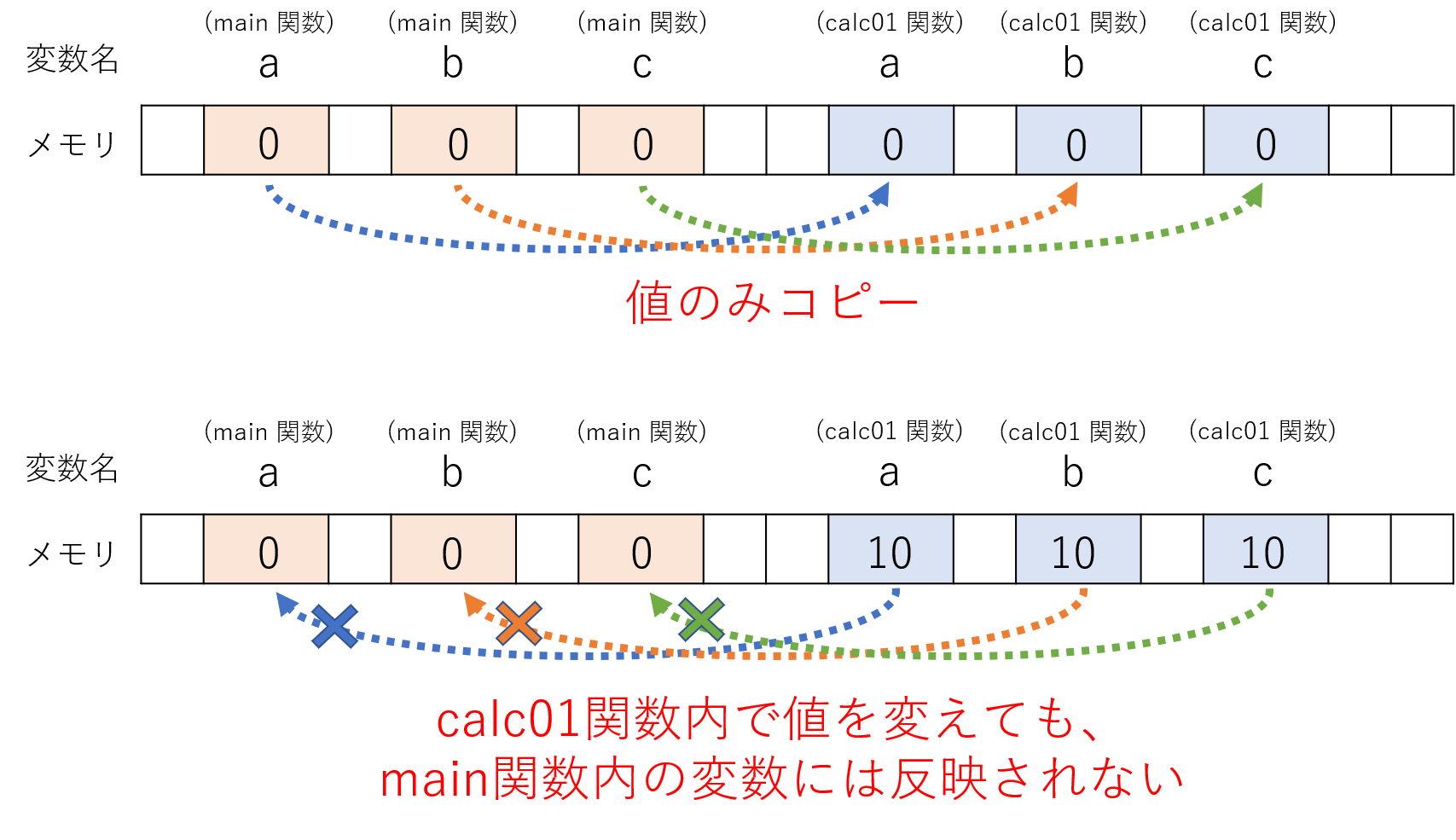
ちなみに、変数名を同じにしてもうまく行きません。 例えば、以下の様にしてもダメです。

#include <stdio.h>
#include <stdlib.h>
void calc01(int a, int b, int plus, int absplus, int mult);
int main()
{
  int plus, absplus, mult;
  plus = 0; absplus = 0; mult = 0;
  calc01(10, -10, plus, absplus, mult);
  printf("%d %d %d\n", plus, absplus, mult);
  return 0;
}
void calc01(int a, int b, int plus, int absplus, int mult)
{
  plus = a + b;
  absplus = abs(a) + abs(b);
  mult = a*b;
}

では、どのようにすればよいのでしょうか？ 関数に箱の中身（数値）を渡すのではなく、箱自体を渡して、その箱に値を入れてもらえば良いのです。 より正確には、箱の位置を教えることで、その場所に計算結果を入れてもらう事ができます。 それがポインタです。 次のプログラムは、期待通りに動きます。

#include <stdio.h>
#include <stdlib.h>
void calc01(int a, int b, int *plus, int *absplus, int *mult);
int main()
{
  int a, b, c;
  a = 0; b = 0; c = 0;
  calc01(10, -10, &a, &b, &c);
  printf("%d %d %d\n", a, b, c);
   
  return 0;
}
void calc01(int a, int b, int *plus, int *absplus, int *mult)
{
  *plus = a + b;
  *absplus = abs(a) + abs(b);
  *mult = a*b;
}

これまで出てこなかった * や & が出てきました。 （&　は scanf 関数で出てきましたが、同じ理由で出てきました。）

int *plus;

で plus という名前の整数型変数へのポインタを定義します。 「整数型変数へのポインタ」とは整数型変数の位置（アドレス）を格納する変数です。

int a;

で定義された整数型変数について、その値が保管されるメモリ上の位置をアドレスと呼びますが、 それは &a で表されます。 つまり、このプログラムでは、関数 calc01 に main 関数内の変数 a, b, c のアドレスを渡す事で、 その場所に直接結果を書き込んでいます。

また、

int *plus;

で定義されたポインタ変数に「値」を代入するには

*plus = 10;

という風に最初に * をつけます。

次の例を見てみましょう。

#include <stdio.h>

int main()
{
  int a = 11;
  int *b;
   
  b = &a;
   
  printf ("%d\n", *b);

  *b = 22;
   
  printf("%d\n", a);
   
  return 0;
}

実行すると、1行目に 11、2行目に 22と表示されます。この例では、

b = &a;

によって、b に a のアドレスを代入しています。 1回目の printf 関数で b の中身（「値」）を表示すると、最初に a に代入された 11 が表示されます。 （b の「値」は、*b と書くことに注意。）その後、

*b = 22;

によって、b の「値」を変更しています。 先のアドレスの代入によって、「a に対して代入すること」と「*b に対して代入すること」が同じ意味となっているので、 2回目の printf 関数で a を表示すると、*b によって更新された値である 22 が表示されます。

◎課題1

方程式 x3 - 2 x2 = 0 の x=2 についての近似解を二分法で計算し、 近似解の変化をgnuplotでグラフとして描画し、表示したグラフを画像ファイルとして出力せよ。 （Bisec-2.c のように a,b,c の変化をそれぞれ描画して下さい）

ちなみに、この方程式には x=0 という解も存在しますが、こちらの解は初期値をうまくとらない限り求めることができません。 理由は、x=0 が重解だからです。二分法は、求める解の近傍で関数の値の正負（符号）が変化することを前提にしていますが、 x=0 の近傍では符号が変化しません。 そのため、二分法でうまく近似解を求めることができません （初期値を -1.0 と 1.0 のようにうまくとれば求めることはできますが。。。）

◎課題2

以下の仕様を満たす関数（ある値が素数かどうか判定する関数）を用いて、 1000以下の奇数のうち素数で無いものを全て求め、 それらを画面に表示し、かつそれらの和も画面に表示するプログラムを作成せよ。

関数の仕様は以下の通り。

関数名： int PrimeNumber(int n)

仕様： 引数として整数 n を受け取り、それが素数であれば戻り値として 1 を返し、n が素数ではないまたは負である場合には -1 を返す

ヒント
for文で繰り返す際に、奇数だけを変数として使いたい場合には

余裕のある人は、さらに以下について答えよ。

素数かどうか判定する関数について、異なるアルゴリズムを用いて複数作成せよ。 さらに、上記の課題を「100000以下の奇数のうち素数でないもの」として、異なるアルゴリズムを用いた関数で計算し、 それぞれの場合のプログラムの実行速度を比較してみよ。

参考

ある2以上の整数 n が素数かどうか判定するアルゴリズムについては、色々と考えられるが、 例えば以下の2つを考えてみよう。

アルゴリズム1

アルゴリズム2

アルゴリズム2の理屈としては、n が n =xyと約数の積で表せるとき、x, y の両方が √ n より小さいことはあり得ない。 同様に、x, y の両方が √ n より大きいこともあり得ない。 つまり、x,y のどちらかは √ n 以上で、もう一方は √ n 以下である。 よって、n が素数でなければ、i を 2 から √ n まで動かす間に、n は i で割り切れるはずである。 また、n が素数でなければ必ず約数の1つは素数になるので、n を 2 から √ n までの素数で割って確かめれば十分である。 また、判定の結果得られた素数は、配列を使って覚えておくことで、上記のアルゴリズム内で活用できる。

◎課題３

5つの実数の入力（scanf関数で入力）に対して、それらの実数の最大値、最小値、平均値を求める関数を作成し、 求めた値を表示するプログラムを作成せよ。 その際、最大値、最小値、平均値をポインタ変数として作成する関数の引数にせよ。

ヒント

計算する関数は、例えば以下の様にすると良い。

関数名：Calculation( double data[5], double *mx, double *mn, double *av)

関数の引数はそれぞれ以下の通りである。

data[5]：入力した5つの実数を格納した配列
mx：最大値のポインタ変数
mn：最小値のポインタ変数
av：平均値のポインタ変数

関数Calculation内で、ポインタ変数 mx, mn, av を用いて計算を行えば、 関数を呼び出したmain関数内での変数の値も更新される。 計算の際には、mx, mn, av がポインタ変数であることに注意（通常の変数の場合と表記が異なることを思い出す）。

ソースコードの例（一部消してあります）

// 最大値最小値平均値
#include <stdio.h>

void Calculation( double data[5], double *mx, double *mn, double *av );

int main()
{
    int i;
    double data[5];
    double Max = 0.0;
    double Min = 0.0;
    double Ave = 0.0;

    // データの入力
    for(i=0; i<5; i++){
        printf("%d つ目の実数を入力してください：", i+1);
        scanf("%lf", &data[i]);
    }

    // 最大値、最小値、平均値の計算
    /* ここで、関数 Calculation を適切な引数を指定して呼び出す */

    // 計算結果の表示
    printf("最大値：%lf\n最小値：%lf\n平均値：%lf\n", Max, Min, Ave);


    return 0;
}

// 与えられた５つのデータの最大値、最小値、平均値を計算する関数
// data:データ　mx:最大値　mn:最小値　av:平均値
void Calculation( double data[5], double *mx, double *mn, double *av )
{
    /*
    ここに関数の中身のコードを書く
    */
    return;
}

課題の提出

「課題1」で作成した画像ファイルと「課題２および課題３」において作成したプログラムを提出してください。
ファイル名は、課題２は 02-rep2.c、課題３は 02-rep3.cとしてください。 画像ファイルの名前は特に指定しません。
ただし、コメント文としてソースプログラムの先頭に

学生番号、名前　を書き込むこと。

また、提出したファイルが正しいものであるかどうかは、毎回確認するよう習慣づけてください。

提出締め切り：　2024年9月30日19時

戻る