前回にGLSC3D利用の準備ができていない人は、前回の内容に従って 速やかに利用できるようにしてください。 分からなければ、すみやかに教員に質問すること。
2024年9月に新たな MacOS 15 (Sequoia) がリリースされました。 OS をバージョンアップした人は、Xcode の更新作業等が必要になる可能性があります。 現在の14 (Sonoma) を使い続けても全く問題ありません。 15へのメジャーアップデートは他の授業で使う予定のソフトウェアへの影響等も考えられるので、 推奨しません。 こちらでも対応できる保証は全くないので、自分で対応できる場合以外はアップデートしない方が良いでしょう。
なお、現在の14を使い続けても全く問題ありませんが、14のセキュリティアップデートは行うようにしてください。
GLSC3Dでは、前回学んだ標準座標系の他に 自由座標系を定義し利用することができます(旧GLSCでは仮想座標系と呼んでいました)。 しかも、自由座標系はいくつでも(もちろん限界はありますが)定義することができます。 2次元の自由座標系を定義するには g_def_scale_2D という関数を使います。
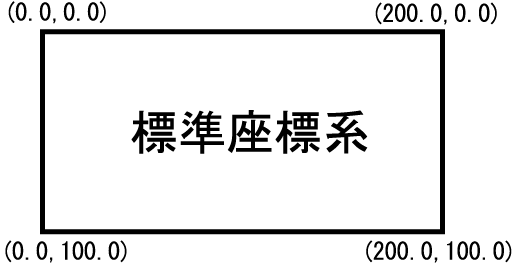
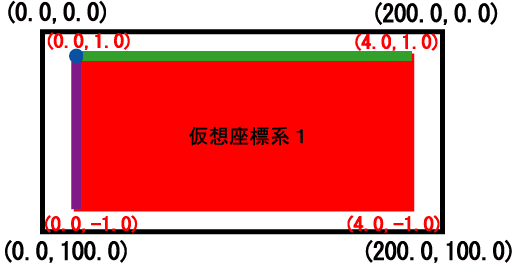
前回扱った標準座標系は、例えば g_init("Test", 200, 100) と初期化されたウィンドウでは、次の図のようになりました。

つまり、左上が座標 (0, 0) であり、右下が (200, 100) となるような座標系です。 例えば、y = sin(x) のグラフを 0 < x < 4 の範囲で描きたい場合、 標準座標系にそのようなグラフを描くには、座標変換の手続きが必要となります。 それではいちいち紛らわしいので、この場合には次のような座標系となっていれば便利です。 (GLSC3Dが自動的に画面上に描画するための座標変換を行ってくれるということです。)
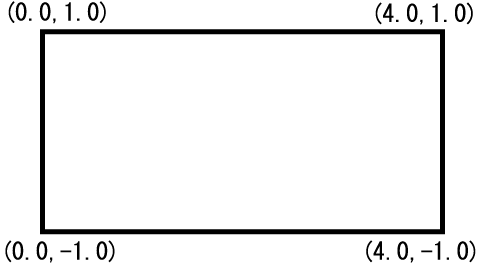
座標系が上図の様になっていれば、y = sin(x) のグラフを描くのも簡単です。 そのような座標系になっていれば、y = sin(x) のグラフを枠内にきちんと収まる形で描けることは容易に想像できるでしょう。 ちょうど、手書きのグラフを描くときに、方眼紙に目盛りを書き込むのに似ています。 GLSC3Dでは、このような座標系を先のウィンドウ内にいくつでも作ることができます。 そして、実際に GLSC3D で絵を描く場合、この座標系(自由座標系と呼びます)を用います。 先の標準座標系は、文字列の描画時と自由座標系の定義時にのみ使います。 (自由座標系をウィンドウ内に定義する場合には何らかの座標系が必要です。標準座標系はその為にあるものだと考えてください。 ちなみにGLSC3Dでは文字列描画は自由座標でも可能。)
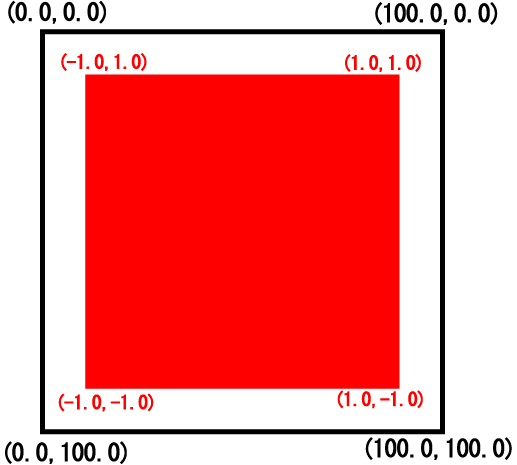
例えば、先の標準座標系の中に1つの自由座標系を定義した場合のイメージを次に示します。
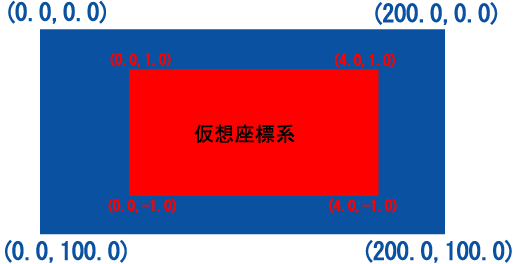
青色が、GLSC3Dのウィンドウ全体をあらわしています。 その中に赤色の自由座標系が定義されている様子を示しています。 このような自由座標系は次の g_def_scale_2D 関数を用いて定義することができます。
GLSC3Dのウィンドウ内に長方形領域を定義して、その長方形内に二次元の座標系を定義する関数が g_def_scale_2d 関数です。 ウィンドウ内に長方形を定義するには、 長方形の位置と大きさを 指定する必要があります。 また、新たに作成する自由座標系の左端、右端、下端、上端の値(x軸およびy軸の範囲)を指定する必要があります。 つまり、長方形の位置と大きさを指定するための4つの値と、自由座標系の範囲を指定するための4つの値で、計8つの値が必要となります。 さらに、自由座標系はいくつでも定義できるので、どの自由座標系の定義であるかを示す通し番号も必要となります。 つまり、g_def_scale_2D 関数には、全部で9つの引数があります。
GLSC3Dマニュアルの g_def_scale_2D 関数の説明部分(p.47)には、 以下のように記載されています。 このように、GLSC3D の関数は引数が多いので、関数利用の際にはマニュアルを参照してください。
g_def_scale_2D:
| id | 整数 | スケール番号。 |
| x_0 | 実数 | 自由座標系での x 座標左端 |
| x_1 | 実数 | 自由座標系での x 座標右端 |
| y_0 | 実数 | 自由座標系での y 座標下端 |
| y_1 | 実数 | 自由座標系での y 座標上端 |
| x_left_std | 実数 | 標準座標系に定義する描画枠の左端の x 座標 |
| y_top_std | 実数 | 標準座標系に定義する描画枠の左端の y 座標 |
| width_std | 実数 | 標準座標系に定義する描画枠の幅 |
| height_std | 実数 | 標準座標系に定義する描画枠の高さ |
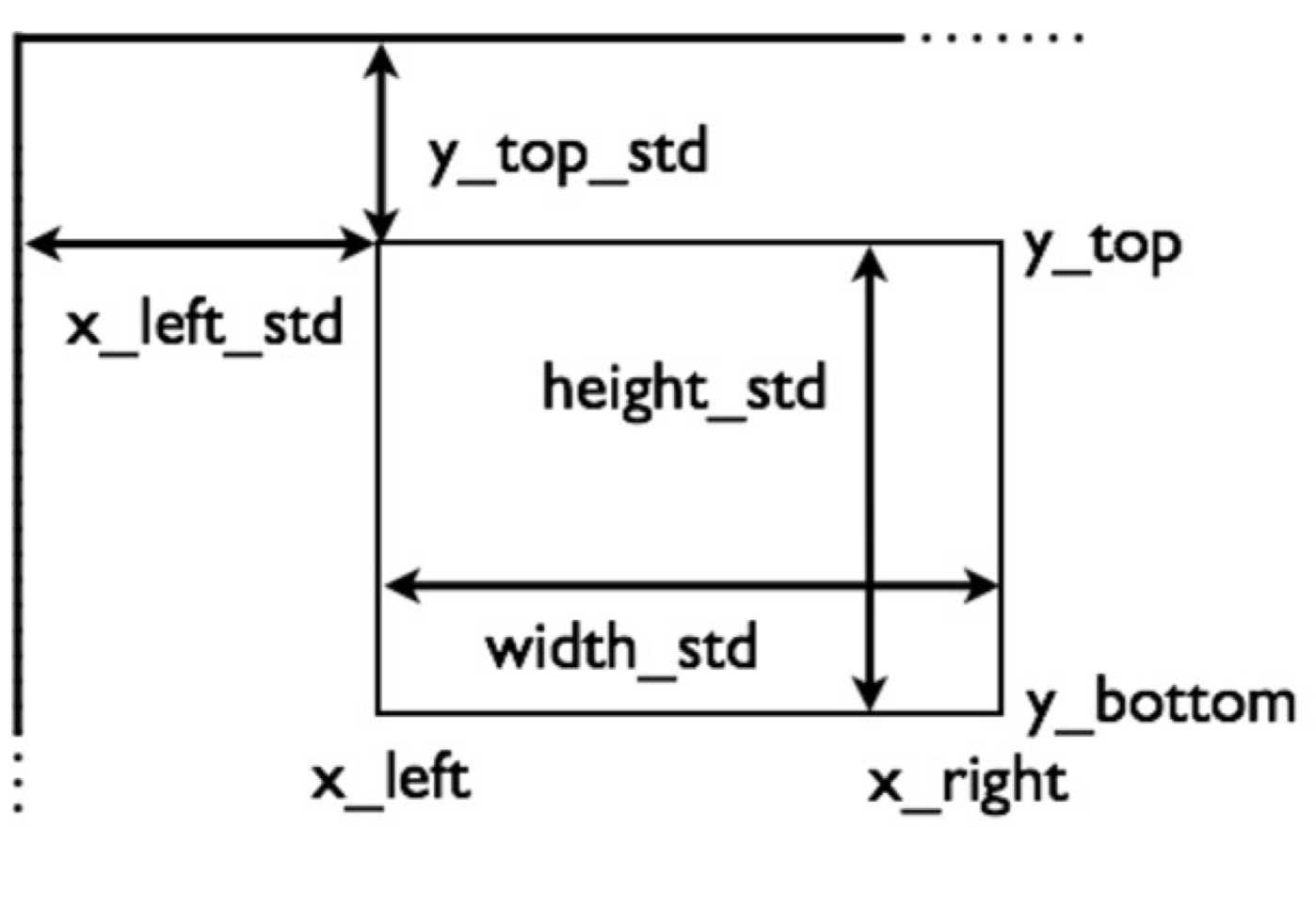
はじめの引数は、これから定義する自由座標系につける通し番号です。 2、3、4、5番目の引数は、自由座標系の左端、右端、下端、上端の値であり、 6、7、8、9番目の引数は、自由座標系の位置と大きさを標準座標系で与えます。 長方形の位置と大きさは、4頂点の座標を与えるのではなく、長方形の左上の標準座標系での座標と、 長方形の幅と高さを与えることに注意してください。
では実際に g_def_scale_2D 関数をつかったサンプルプログラムを見てみましょう。
#include <glsc3d_3.h>
#include <stdio.h>
int main()
{
g_init("Test", 200.0, 100.0);
g_def_scale_2D(1, 0.0, 4.0, -1.0, 1.0, 10.0,
10.0, 180.0, 80.0);
g_cls();
g_finish();
g_sleep(10);
return 0;
}
このプログラムでは、次のような自由座標系を定義しています。
コンパイルして実行してみても、ただウィンドウが表示されるだけですが、実際には自由座標系が定義されています。 そこで次に、自由座標系に図形を描いてみることにします。
GLSC3D では、 g_circle_2D 関数で円を描画することができます。 g_circle_2D には5つの引数があり、はじめの2つで円の中心位置を自由座標系で指定します。 3つめの引数は、描く円の半径となります。 4つめの引数は円のふちを描くかどうかの指定(G_YES または G_NO)で、5つめの引数は円の内部を塗りつぶすかどうかの指定(G_YES または G_NO)を行います。
#include <glsc3d_3.h>
#include <stdio.h>
int main()
{
g_init("Circle", 100, 100);
g_def_scale_2D(1, -1.0, 1.0, -1.0, 1.0, 10.0, 10.0, 80.0, 80.0);
g_cls();
g_sel_scale(1);
g_circle_2D(0.0, 0.0, 0.5, G_YES, G_NO);
g_finish();
g_sleep(10);
return 0;
}
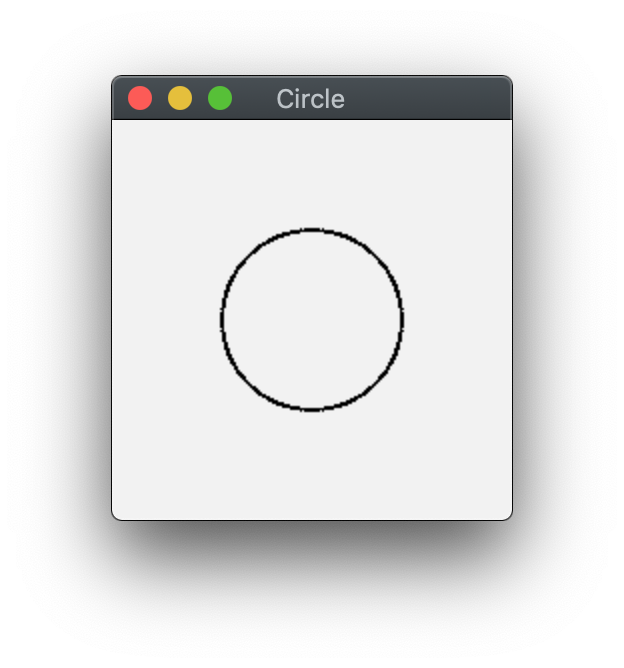
上のプログラムでは、以下のような自由座標系(赤色で示した)を1番(g_def_scale_2D の第一引数)として定義しています。 この自由想座標系に絵を描きたいので、これを選ぶために g_sel_scale 関数で1番の自由座標系を選びます。 その後、g_circle 関数で円を描きます。 このように、自由座標系がたった一つであっても、g_sel_scale で一度選ぶ必要があります。 g_def_scale_2D 関数と g_sel_scale 関数は GLSC3D プログラムには必ず出てくると思ってください。
プログラムの実行結果は次のようになります。
次に、2つの自由座標系を定義して、使ってみましょう。 以下の例では、標準座標系上の全く同じ位置に、同じ大きさの自由座標系を作っています。 ただし、座標のスケールが異なります。
#include <glsc3d_3.h>
#include <stdio.h>
int main()
{
g_init("circle2", 100, 100);
g_def_scale_2D(1, -1.0, 1.0, -1.0, 1.0, 10.0, 10.0, 80.0, 80.0);
g_def_scale_2D(2, -2.0, 2.0, -2.0, 2.0, 10.0, 10.0, 80.0, 80.0);
g_cls();
g_sel_scale(1);
g_circle_2D(0.0, 0.0, 0.5, G_YES, G_NO);
g_sel_scale(2);
g_circle_2D(0.0, 0.0, 0.5, G_YES, G_NO);
g_finish();
g_sleep(10);
return 0;
}
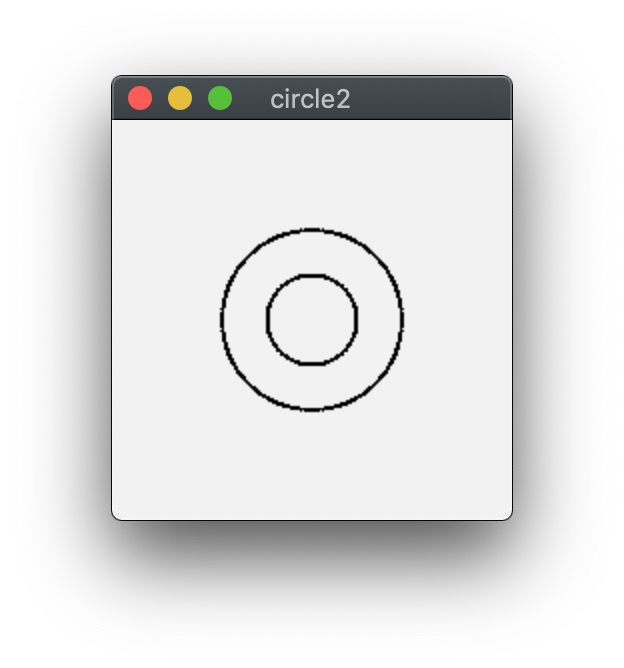
実行結果は次のようになります。2つの g_circle_2D は全く同じなのに(位置、半径が同じ)、2つの見た目違う半径の円が描かれました。
異なる自由座標系を用いて描いているからですが、その意味をよく理解してください。
2つ目の自由座標系は、1つ目のものと比べて2倍の領域で定義されているので、同じ半径の円でも描画される円の大きさは半分になります。
(旧GLSCと異なり、自由座標系をうまくとれば、楕円を描くことも可能です。)
また、円に色をつけることもできます。 g_area_color 関数で、円内部の塗りつぶし色を指定し、 g_line_color 関数でふちの線色を指定します。 色の指定は、前回使った g_text_color 関数と同様に、赤・緑・青・不透明度を指定します。 2つ目の g_circle_2D では、内部塗りつぶしをしない(5つ目の引数が G_NO である)ので先に描かれた赤色が残っています (5つ目の引数を G_YES に変更してみよ)。
#include <glsc3d_3.h>
#include <stdio.h>
int main()
{
g_init("circle3", 100, 100);
g_def_scale_2D(1, -1.0, 1.0, -1.0, 1.0, 10.0, 10.0, 80.0, 80.0);
g_def_scale_2D(2, -2.0, 2.0, -2.0, 2.0, 10.0, 10.0, 80.0, 80.0);
g_cls();
g_sel_scale(1);
g_area_color(1.0, 0.0, 0.0, 1.0);
g_line_color(0.0, 0.0, 1.0, 1.0);
g_circle_2D(0.0, 0.0, 0.5, G_YES, G_YES);
g_sel_scale(2);
g_area_color(0.0, 1.0, 0.0, 1.0);
g_line_color(0.0, 1.0, 0.0, 1.0);
g_circle_2D(0.0, 0.0, 0.5, G_YES, G_NO);
g_finish();
g_sleep(10);
return 0;
}


g_box_2D 関数により、四角形を描くことができます。 g_box_2D 関数の使い方はGLSC3Dマニュアルの p.70 を参考にしてください。 g_circle_2D 関数の使い方が理解できていれば、問題なく理解できるはずです。
g_move_2D 関数と g_plot_2D 関数を用いると、直線を描くことができます。
g_move_2D 関数で直線の始点を指定し、g_plot_2D 関数で直線の終点を指定します。
また、g_line_color 関数で直線の色を指定でき、
g_line_width 関数で直線の幅を指定できます。
(それぞれマニュアル参照 g_move_2D, g_plot_2D は p.69 g_line_color, g_line_width は p.60)
#include <glsc3d_3.h>
#include <stdio.h>
int main()
{
g_init("Line", 200, 200);
g_def_scale_2D(1, -1.0, 1.0, -1.0, 1.0, 10.0, 10.0, 180.0, 180.0);
g_cls();
g_sel_scale(1);
g_area_color(0.0, 0.0, 1.0, 1.0);
g_line_color(0.0, 0.0, 1.0, 1.0);
g_circle_2D(0.0, 0.0, 0.5, G_YES, G_YES);
g_line_color(1.0, 1.0, 0.0, 1.0);
g_line_width(3);
g_move_2D(-1.0, -1.0);
g_plot_2D(1.0, 1.0);
g_line_color(0.0, 0.0, 0.0, 1.0);
g_line_width(1);
g_move_2D(-1.0, 1.0);
g_plot_2D(1.0, -1.0);
g_finish();
g_sleep(10);
return 0;
}

g_plot_2D を連続してプログラム中に書くと、連続した直線を描く事ができます。 直前のプログラムの2つ目の g_move_2D を消去した次のプログラムでは、以下のような結果となります (実際に2つ目の g_move_2D 関数を消去(コメントアウト)して試してみよ)。
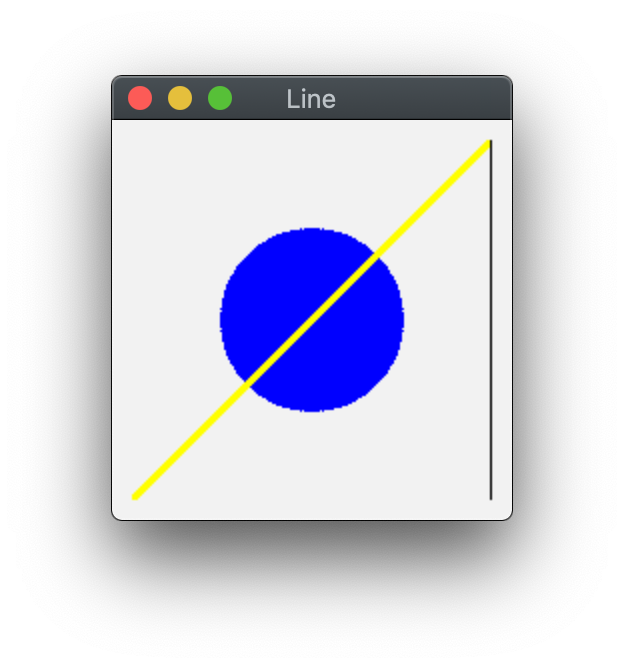
つまり、直前の g_plot_2D 関数で指定された座標を始点とする直線が引かれます。
円が時間と共に移動するアニメーションプログラムを作成せよ。 ただし、領域の端に到達したら跳ね返り、色が変わるようにすること。 (簡単そうに見えて、結構難しいかも)
次に、GLSC3Dを使って y = sin(x) のグラフを描いてみましょう。 実際には、y = sin(x) のグラフは滑らかな曲線ですが、 コンピュータではそのような滑らかな曲線を直接は扱えないので、折れ線で近似します。 つまり、変数 x は実際には連続的に変化する値ですが、とびとびの値を使います。 後の例で見るように、とびとびとはいえ区間を十分に細かく取れば、折れ線で曲線をうまく近似することができます。
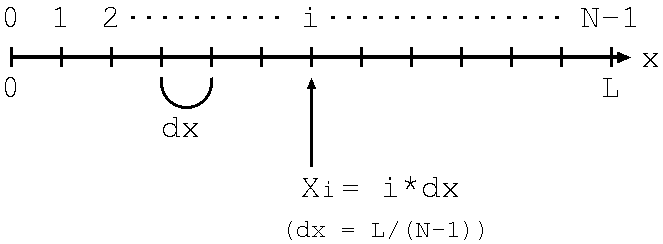
図のように、[0, L] 区間を N-1 等分して、その等分した小区間の幅を dx とします。 N-1 等分すると図のように N 個の区切りが現れますが、それらに 0,1, ...., i, ...., N-1 と番号をつけることにします。 また、N を分割数、dx を分割幅と呼びます。 このとき、
Xi = i * dx
の部分についてそれぞれ y = sin( Xi ) を計算し、それらを折れ線で結ぶことを考えます。 C言語風に書けば
X[i] = dx * i;
Y[i] = sin( X[i] );
をそれぞれ求め、(X[0], Y[0]), (X[1],Y[1]), ...., (X[N-1], Y[N-1]) を結ぶ折れ線を描くことになります。 これをプログラムにすると以下のようになります。 (上記の説明にあわせるためにかなり無駄なことをしています。) 自分で以下のソースコードを打ち込み(コピペし)、実行してみてください。
注意: 数学関数(sin, cos, tan 等)を使う場合には、#include <math.h>(math.h をインクルード)が必要となります。
#include <glsc3d_3.h>
#include <stdio.h>
// 次の文は数学関数を使う場合に必要
#include <math.h>
// 定数の定義
#define N (5)
#define PI (3.1415926)
#define L (2*PI)
int main()
{
int i;
double X[N], Y[N], dx;
// dx を求める
dx = L/(N - 1);
// GLSCの初期化
g_init("Sine Curve", 400, 200);
// 自由座標系の定義
g_def_scale_2D(1, 0.0, L, -1.0, 1.0, 20.0, 20.0, 360.0, 160.0);
g_cls();
// 外枠の描画
g_sel_scale(1);
g_area_color(1.0, 1.0, 1.0, 1.0);
g_line_color(0.0, 0.0, 0.0, 1.0);
g_line_width(2);
g_box_2D(0.0, L, -1.0, 1.0, G_YES, G_YES);
// x軸の描画
g_move_2D(0.0, 0.0);
g_plot_2D(L, 0.0);
// y軸の描画
g_move_2D(L/2.0, 1.0);
g_plot_2D(L/2.0, -1.0);
// X[i] を計算
for(i = 0; i < N; i++)
{
X[i] = i*dx;
}
// Y[i] を計算
for(i = 0; i < N; i++)
{
Y[i] = sin(X[i]);
}
// 折れ線を描く
g_line_color(1.0, 0.0, 0.0, 1.0);
g_line_type(0);
g_line_width(2);
g_move_2D(X[0], Y[0]);
for(i = 1; i < N; i++)
{
g_plot_2D(X[i], Y[i]);
}
g_finish();
g_sleep(100);
return 0;
}
上記プログラムに、グラフの左端右端等の情報を書き入れたプログラムの出力を使って、N の値とグラフの関係を見てみましょう。 青色の破線で書かれたグラフが描きたいグラフ y = sin(x) です (とはいっても、もちろんこれも N=100 での折れ線です)。 赤色の実線が描こうとしている折れ線です。
N=5 の場合は以下のようになります(赤線)。 これでは、まったく y = sin(x) のグラフには見えません。
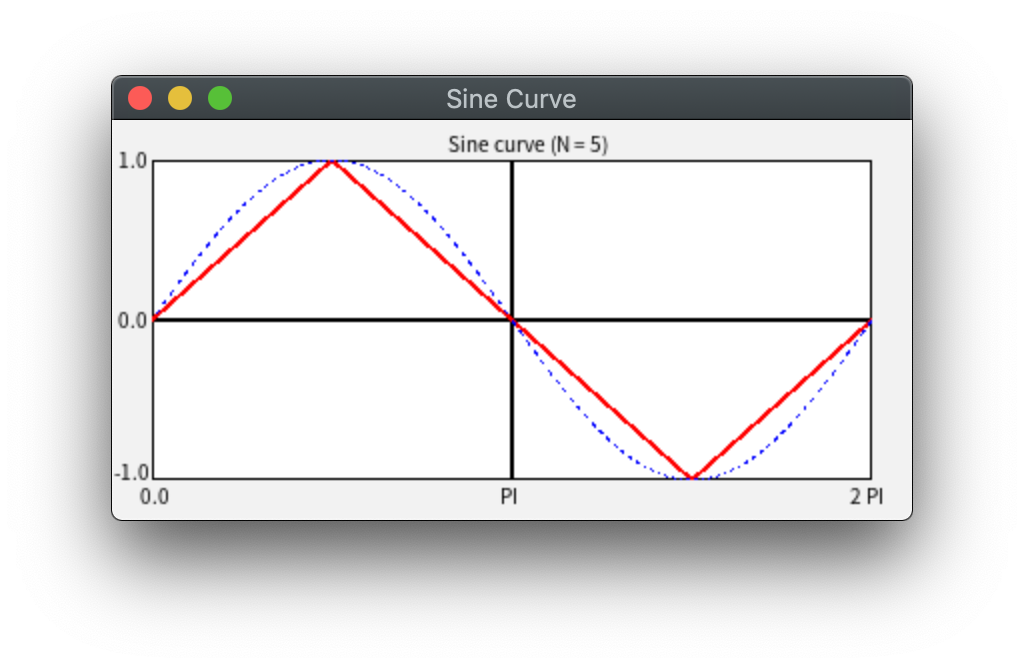
つづいて、N=10 の場合(赤線)。曲線っぽくみえてきました。
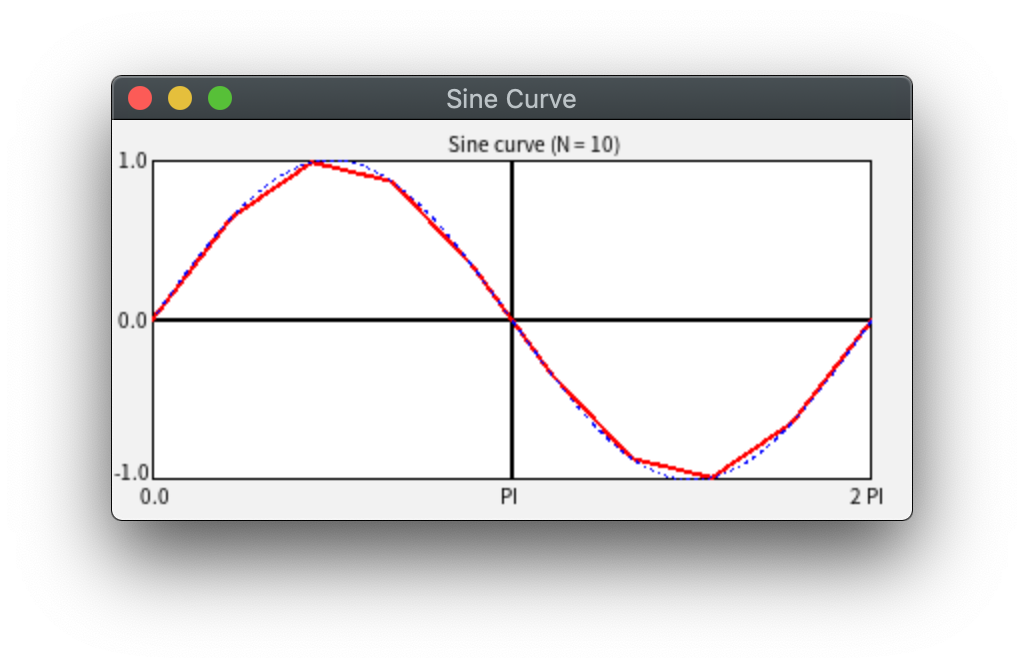
N=50 の場合(赤線)。見た目はほぼ y=sin(x) のグラフに見えます。
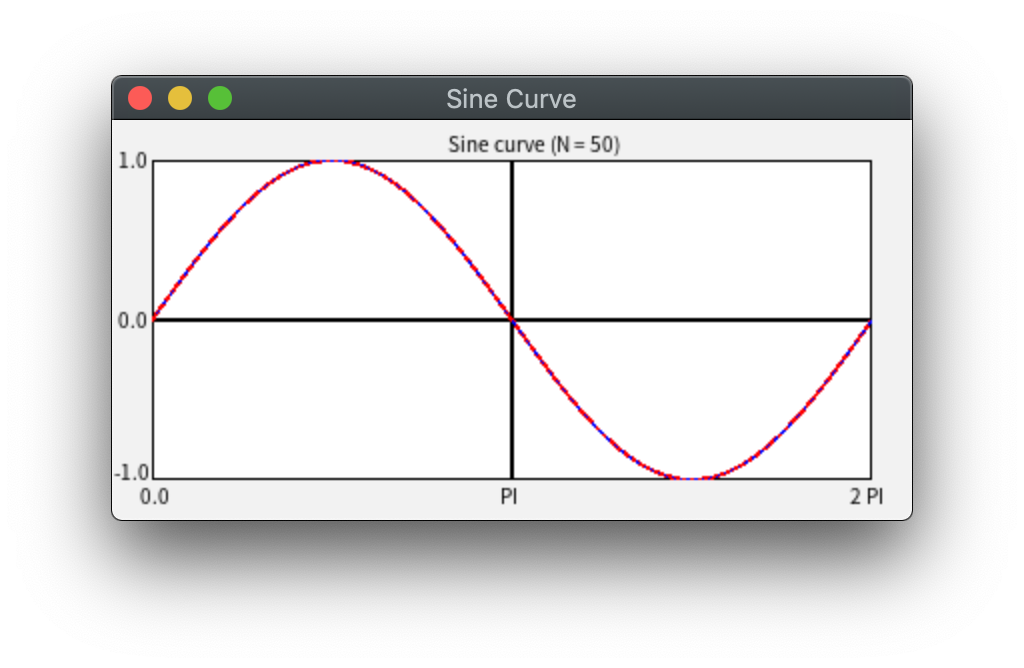
自由座標系を2つ用意し、scanf関数で入力した k の値を用いて、下の図のように、
y = sin(k*x) のグラフと y = cos(k*x) のグラフをそれぞれの自由座標系に対して描け。
(下図ではN=100のグラフを重ねて表示しているが、これは描かなくても良い。できそうなら試してください)
このとき、必ず自由座標系を2つ用意し、グラフのタイトル、縦軸と横軸の値も表示すること。
自由座標系を使えば、cosの方はsinのほぼコピペでできる!)
ヒント
自由座標系を2つ使うには、文字列については、前回の文字列の描画(その2)で説明した手法 を用いて書くと良い。 また、文字列の描画についてはg_text_standard 関数(標準座標系での配置)、 あるいは g_text_2D_virtual 関数(自由座標系での配置)を用いる。
おまけ
k の値を大きくすると、正確なグラフが表示されなくなることを確かめてみよ。 また、なぜそうなるのか理由を考えてみよ。

前回アニメーションの作り方を学んだので簡単です。 ここでは、t は時間として扱いますが、当然連続量として扱うことができないので、先ほどまでの x 同様、とびとびの値(離散値)として扱います。 先ほどの x と同様に考え、t の範囲を [0, T] として、それを K-1 等分します。 その小区間の幅を dt として(つまり、 dt = T/(K-1))、
Tk = dt * k
とすることにより、 Tk を止めるごとに Y[i] = sin(Xi + Tk) のグラフを描くことを繰り返せば、アニメーションとなります。 以下のサンプルプログラムを打ち込み(コピペし)、実行してみてください。 これまでのアニメーションプログラムと仕組みが同じであることに気づくことが重要です。
#include <glsc3d_3.h>
#include <stdio.h>
#include <math.h>
// 定数の定義
#define N (50)
#define K (100)
#define PI (3.1415926)
#define L (2*PI)
#define T (10.0)
int main()
{
int i, k;
double Y[N], dx;
double dt;
// dx, dt を計算
dx = L/(N - 1);
dt = T/(K - 1);
// GLSCの初期化
g_init("Moving Sine Cruve", 400, 200);
// 自由座標系の定義
g_def_scale_2D(1, 0.0, L, -1.0, 1.0, 20.0, 20.0, 360.0, 160.0);
for(k = 0; k < K; k++)
{
g_cls();
// 描画する自由座標系の選択
g_sel_scale(1);
// 外枠の描画
g_area_color(1.0, 1.0, 1.0, 1.0);
g_line_color(0.0, 0.0, 0.0, 1.0);
g_line_type(0);
g_line_width(2);
g_box_2D(0.0, L, -1.0, 1.0, G_YES, G_YES);
// x軸の描画
g_move_2D(0.0, 0.0);
g_plot_2D(L, 0.0);
// y軸の描画
g_move_2D(L/2.0, 1.0);
g_plot_2D(L/2.0, -1.0);
// Y[i] を計算
for(i = 0; i < N; i++)
{
Y[i] = sin(i*dx + k*dt);
}
// 折れ線を描く
g_line_color(1.0, 0.0, 0.0, 1.0);
g_line_type(0);
g_line_width(1);
g_move_2D(0.0, Y[0]);
for(i = 1; i < N; i++)
{
g_plot_2D(i*dx, Y[i]);
}
g_finish();
g_sleep(0.05);
}
g_sleep(10);
return 0;
}
自由座標系を2つ用意して、y=sin(x+t) のグラフのアニメーションと
y=cos(x+t)のグラフのアニメーションが、それぞれの自由座標系に対して描画されるような
プログラムを作成せよ。
(必ず自由座標系を2つ用意し、グラフのタイトル、縦軸と横軸の値も表示すること。)
ヒント
基本方針は課題1と全く同じ。 違いは、アニメーションなので描画についての部分が for 文内に入っているだけ。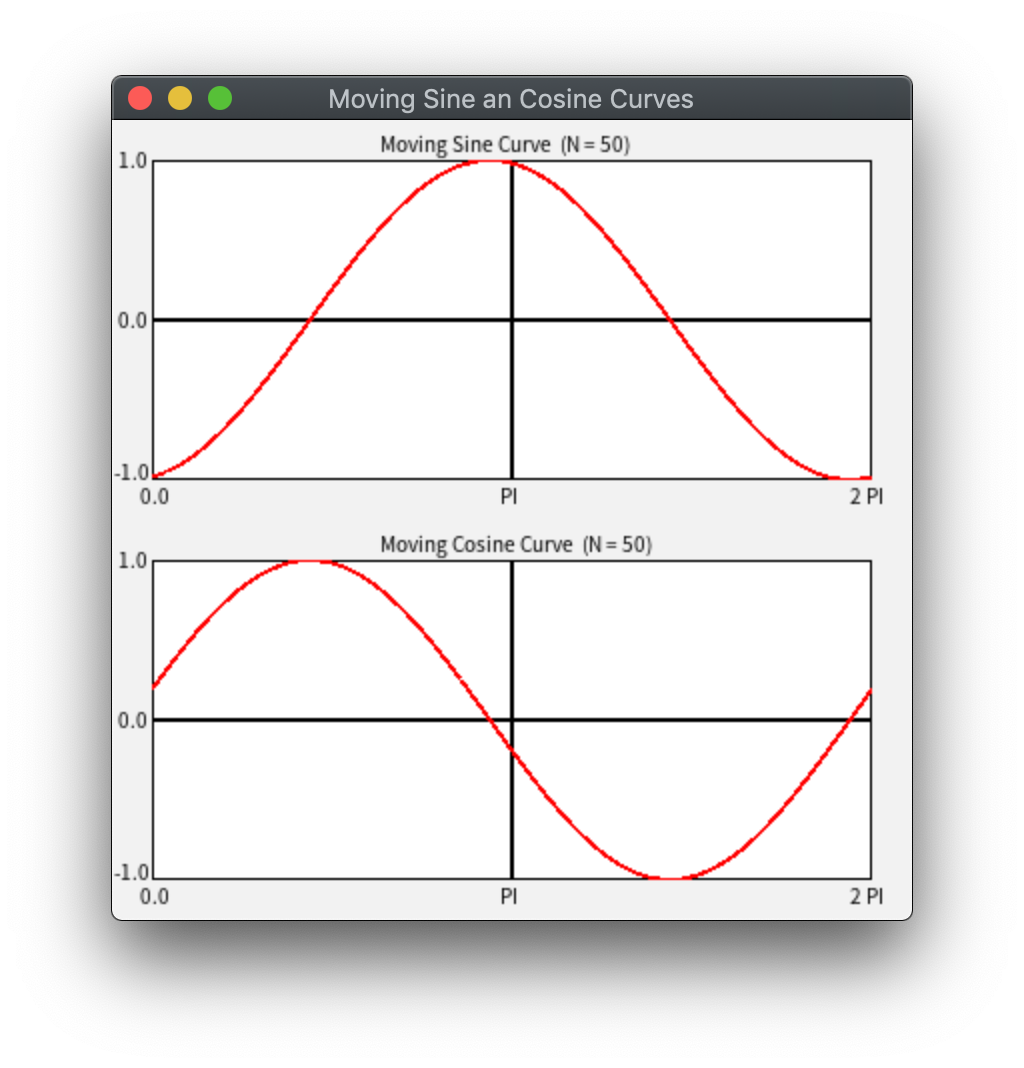
以下のような図形(リサジュー図形)を描くプログラムを作成せよ。 さらに、曲線を描く過程をアニメーションで表示せよ。
ヒント
「曲線を描く過程」をアニメーションにするためには、 各ステップごとに「それまでの時刻の時刻の全ての線分」を描く必要があるので、 各線分を繋ぐための全ての点の座標を保存しておく必要がある。 具体的には、アニメーションのための繰り返し(for文)の中に、 それまでの線分を描くための繰り返し(for文)を入れる。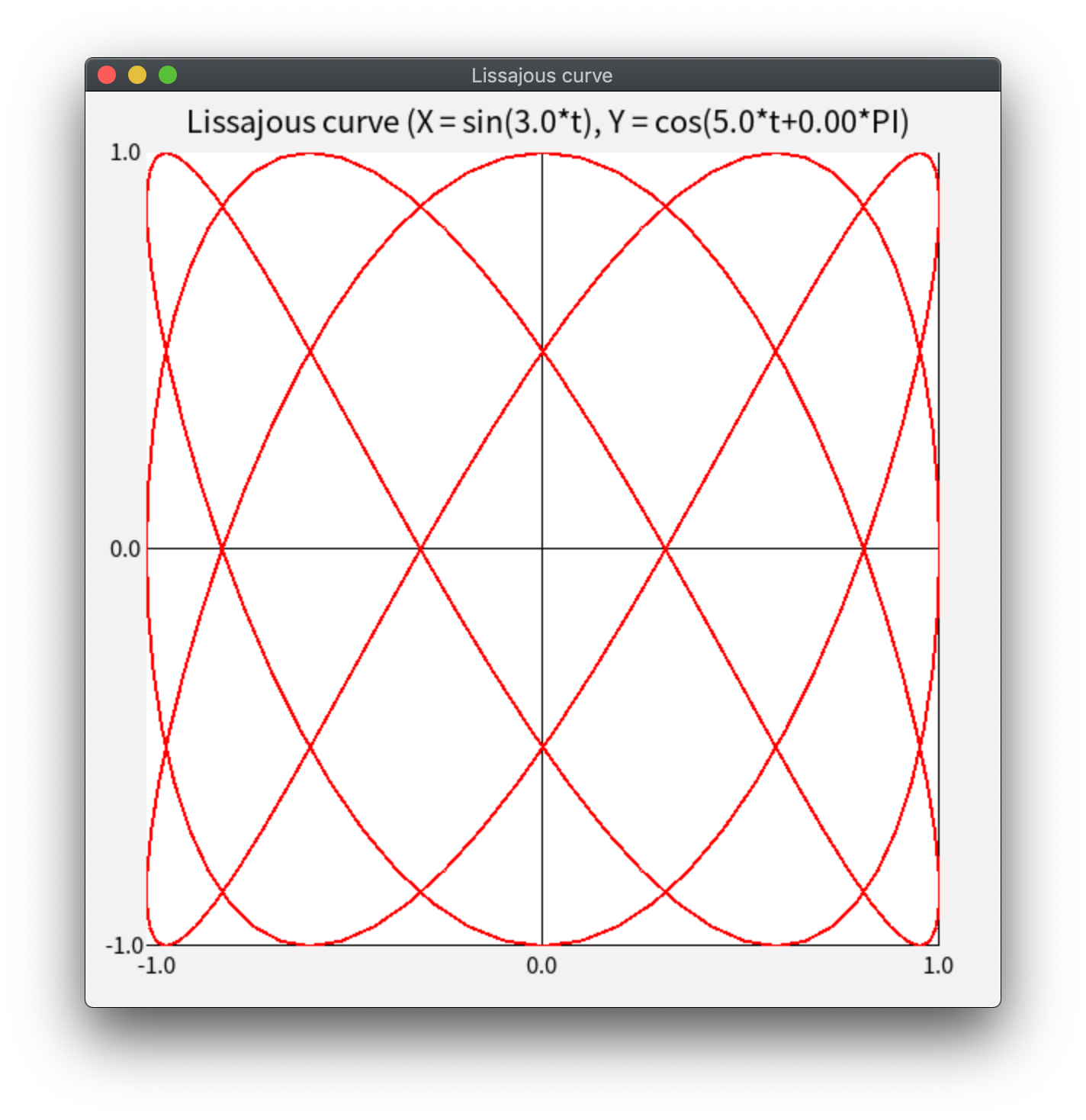
「課題1」、「課題2」、「課題3」で作成したプログラムのうち、最低どれか2つを提出してください。
(課題3については、課題1、2が簡単だという人向けです。
課題1、2は確実にできるようになって欲しいので、それが問題なくできる人が取り組んでください。)
ただし、コメント文として、
学生番号、名前、プログラムの説明
を書くこと。 ファイル名は、課題1は 04-rep1.c、課題2は 04-rep2.c、課題3は 04-rep3.c として、 ファイル単体でコンパイルできるようにすること。
提出締め切り: 2024年10月14日19時