第6回連立方程式の解法 (1)

来週の授業について

出張のため、来週(6/2)の授業はオンデマンド形式で実施します。

来週の月曜日までに、授業用Webを用意しておきます。各自の都合の良いタイミングで、授業用Webの指示に従って受講してください。出席はとりません。
6/2は、授業時間中も0609教室は利用できませんので、注意してください。
来週に限らない話ですが、質問がある場合はビークルダイナミクス研究室にてTAに質問をすることが可能です。

6.1 ガウス・ジョルダン(Gauss-Jordan)法

以下のような連立一次方程式(ここでは3元一次を例にとる)

の解を数値演算(解析的ではなく、すなわちコンピュータで)により求める。ガウス・ジョルダン法は以下の手順により計算を行う。

(1)式を a₁₁ で割り、x₁の係数を1にする。→ (1)'式
(2)式から、(1)'式をa₂₁倍したものを引く。→ (2)'式
(3)式から、(1)'式をa₃₁倍したものを引く。→ (3)'式

すると、次のように(2)式、(3)式のx₁の係数は0になる。

同様に、

(2)'/a'₂₂ → (2)''
(1)'-(2)''*a'₁₂
(3)'-(2)''*a'₃₂

としてx₂の項を消してゆくと、

となる。さらに、

(3)''/a''₃₃ →(3)'''
(1)''-(3)'''*a''₁₃
(2)''-(3)'''*a''₂₃

としてx₃の項を消していくと、最終的に

となって解を得ることができる。

6.2 具体例

上の作業を具体的な数値を代入して実行してみる。例えば、次のような3元の連立方程式

の場合、以下のような3行4列の係数行列を作って作業することになる。

6.3 プログラム・コーディング

この操作をプログラムとして実現するには、どうすれば良いだろうか？
また、一般にn元の連立方程式を解く場合には、どのようなプログラムを記述すれば良いだろうか？？
プログラミングの際には、以上の操作を 抽象的 あるいは 一般的 に記述する必要があります。

前節の最後の式の左辺が

のように単位行列になっていることに注目しよう。より一般に、n元の連立方程式を取り扱う場合にも、下図のように単位行列が得られるまで「掃き出し演算」を行えばよいことがわかる。

この作業を一般的に記述すると次のようになる。(一般的な作業手順のことをアルゴリズムと呼ぶ)

ピボットが含まれる行に対し、行の要素(a_ii, a_ii+1, ... , a_in, b_i)をピボット係数(a_kk)で割る。結果としてピボットは1となる。なお、ピボットの左側の要素(a_k1, a_k2, ... , a_kk-1)は既に0になっているので割らなくて良い。
ピボット行以外の各行に対し、ピボットと同じ列が消去されるように
(各行の要素)-(ピボット行の要素)×(係数)
の計算を行う。ここで、係数としてはピボットと同じ列の要素を用いれば、ピボットと同じ列が消去されることになる
次の行に移る

サンプルプログラム: gauss_jordan.cpp

6.4 例題

上のサンプルプログラムを修正し、以下の4元1次連立方程式の解をガウス・ジョルダン法により求めよ。

課題 (提出〆切：金曜22時)

mat_Ab.txtには，今回の授業で説明した連立1次方程式 Ax=bを表す係数行列が記述されている。このtxtファイルを読み込み、連立方程式の解をガウス・ジョルダン法により求め、連立方程式の解を画面に出力せよ。
- プログラムのファイル名は6_1.cppとすること。
- ファイルに含まれる係数行列のサイズはあらかじめ分かっているという前提でプログラムを作成して構わない。
- サンプルプログラムの改良を行わずに実行するとプログラムは実行途中で停止する。なぜプログラムが停止するかを考え、対策せよ。
- 読み込むtxtファイルは、プログラム内で指定すること。
- コマンドライン引数は実行ファイル名のみにすること。
- 最終的に下記の例に示した通りに解を出力すること。例はプログラムの実行例を示すものであり、値は適当であるため注意すること。計算過程も画面出力することをおすすめする。
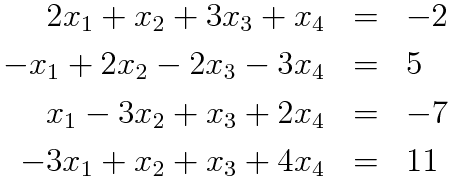
```
Z:\compmech\ex6>6_1.exe
--------- Solutions ---------
x_1 =    12.000
x_2 =   -11.000
x_3 =    14.000
x_4 =   -11.000
```
Output_Mat.cppは、係数行列Aを自動生成し、mat_A_rand.txtというファイル名のtxtファイルとして出力するプログラムである。生成される行列のサイズは、実行するごとにランダムで決定され、3x3から7x7までの範囲で変化する。また、行列の要素も乱数により決定される。この自動生成された行列Aをmat_A_rand.txtから読み込み、その逆行列を求めて画面に出力するプログラムを作成せよ。

プログラムのファイル名は6_2.cppとすること。
Output_Mat.cppをブラウザで表示すると、文字化けします。ファイルをダウンロードし、エディタで開いて確認してください。
ガウス・ジョルダン法を応用すると、以下に述べる「掃き出し法」を用いて逆行列を求めることができる。
6_2_sample.cppは、この課題のプログラムの一部である(こちらも文字化けするので、ファイルをダウンロードして確認してください)。不足している部分やガウス・ジョルダン法を行うプログラム等を補いプログラムを完成させよ。
mat_A_rand.txtに含まれる行列Aは、Output_Mat.exeを実行するたびにサイズが変更されるため、ファイルを読み込む際に行列のサイズを判定する処理を行う必要がある。この処理は、6_2_sample.cppに含まれている。
malloc()関数やnew()関数を利用すると、配列のサイズを動的に調整することができるが、少し難しくなるため、今回はあらかじめ行列Aの最大サイズ(N=7)を想定して配列を宣言している。
作成したプログラムを動作確認する際に行列Aのサイズが異なる場合でも正しく動作することを確認すること。
読み込むtxtファイル名は、プログラム内で指定すること。
コマンドライン引数は実行ファイル名のみにすること。
最終的に下記の例に示した通りに解を出力すること。例はプログラムの実行例を示すものであり、値は適当であるため注意すること。計算過程も画面出力することをおすすめする。

  Z:\compmech\ex6>6_2.exe
  -------- Inverse Matrix --------
   0.343   1.453  -0.661  -1.224  -0.029
  -0.257  -1.376   0.710   1.204  -0.229
  -0.371  -0.955   0.502   1.041   0.114
  -0.114   1.135  -0.494  -0.878   0.343
   0.086  -0.065  -0.094   0.122  -0.257