
グラフの探索
日常的に活用されもっとも抽象化されている概念にグラフ構造がある。 人間関係に代表される同盟と敵対、物品の移動など交通路、町や国など地図の隣接、病気の伝搬、化学反応や食物連鎖、さらには知識や概念の体系など、 世界事象のあらゆる関係性は何らかのグラフ構造として記述されるからである。 このために、グラフを構成する頂点を列挙する探索アルゴリズムは重要な応用に直結する。
グラフ(graph) $G=(V, E)$ とは頂点(vertex)または節(ノード node)の集合 $V=_\{v_1,v_2,\dots,v_n\}$ と頂点 $v_j$ と $v_k$ との結びつきを辺(edge) $e_{jk}$ とする辺の集合 $E=\{\dots, e_{jk},\dots\}$ を指定して定義される。
また、辺の構成において、辺 $e_{jk}$ を頂点 $v_j$ から $v_k$ への結びつきと考えて$v_k$ から $v_j$ への辺 $e_{kj}$ とを区別する有向グラフ(digraph)か無向グラフを区別することは実用上でも重要な場合が多い。 有向グラフの辺は矢印で表す。 頂点からある頂点への辺が高々1本であるグラフを単純(simple)という。 ここでは、主に単純グラフを扱うことにする。
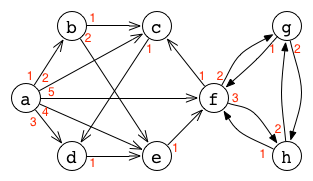 左図は有向グラフを表している。
各頂点に添えられた赤い数字は、隣接する頂点の順番を示している。
左図は有向グラフを表している。
各頂点に添えられた赤い数字は、隣接する頂点の順番を示している。
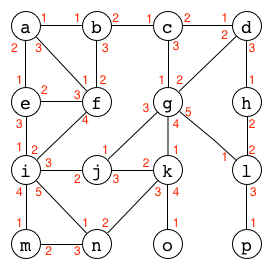 右図は無向グラフを表している。
各頂点に添えられた赤い数字は、隣接する頂点の順番を示している。
右図は無向グラフを表している。
各頂点に添えられた赤い数字は、隣接する頂点の順番を示している。
頂点から1つの辺でつながっている頂点の並びである隣接関係(adjacency relation)が、その並びに順序がついている隣接リスト(adjacency list)である場合と、順序が付いていない隣接集合((adjacency set)で与えられるかによって順序付きグラフ(ordered graph)が順序のない非順序グラフに分けられる。 与えられた頂点から辺で結ばれたどの隣接頂点を選ぶかに受洗順位を付けてあるのが順序付きグラフで、実際的理由から暗黙裡に順序付きグラフを仮定することが多い。
グラフの探索
二分木の探索とその応用については、二分木の探索で紹介した。
グラフ $G=(V, E)$ において、$n$個かならる頂点 $V=\{v_1, v_2,\dots, v_n\}$ を何らかの方法で1回だけ訪れること \[ \text{Search of $G$}= v_{\tau(1)},v_{\tau(2)},\dots ,v_{\tau(n)} \] を$G$の探索(search)または走査(traversal)という。 ここで $\tau$ は $(1,2,\dots, n)$ の並べ替え(permutaion)である。 $n$個の頂点を持つグラフの探索は $n!$ 通りある。
グラフの記述
与えられたグラフを表現するには、頂点とその隣接関係を与えればよい。 順序付きグラフのためには、隣接関係として順序を付けて(数学的には括弧 ( と ) を使って)、頂点 $v_j$ では 1番目が $v_{\ell_j(1)}$ 2番目が $v_{\ell_j(2)}$、...k番目が $v_{\ell_j(k_j)}$ というように並べる。 隣接関係に順序を付けない非順序付きグラフは、隣接する頂点を括弧 { と } で囲って集合として表せばよい。
たとえば、順序付きグラフを表すには次のように与えればよい(括弧 ( と ) を { と } で置き換えると非順序グラフになる)。 \begin{align*} \ell_{v_1}&=(v_{\ell_1(1)},v_{\ell_1(2)},\dots v_{\ell_1(k_1)})\\ \vdots\\ \ell_{v_j}&=(v_{\ell_j(1)},v_{\ell_j(2)},\dots v_{\ell_j(k_j)})\\ \vdots\\ \ell_{v_n}&=(v_{\ell_n(1)},v_{\ell_n(2)},\dots v_{\ell_n(k_n)}) \end{align*}
この隣接関係によるグラフの表し方は、自然に向き付けられた辺を表すことができていることに注意する。 ある頂点 $v_j$ の隣接関係に頂点 $v_k$ が現れ、一方で $v_k$ の隣接関係に $v_j$ が現れないときには、辺は $v_j$ から $v_k$ への $e_{jk}$ があり、$v_k$ から $v_j$ への辺が内ことになるからである。
グラフ $G=(V, E)$ は次のような隣接行列(adjacency matrix)$A(G)$ で表すこともできる。 $n$個の頂点に番号を付けて(ここではPython的に添字を 0 から $n-1$ とした)、$i$番目頂点 $v_i$ と $v_j$ が辺で結ばれていれば行列要素 $a_{i,j}=1$、辺で結ばれていなければ 0 とする。 \[ a_{i,j}=\left\{ \begin{array}{ll} 1 & \text{$v_i$ and $v_j$ is connected}\\ 0 & \text{not connected} \end{array} \right. \] 無向グラフの場合には $a_{i,j}=a_{j,i}$ であるため隣接行列は対称行列となる。 \[ A(G) =\begin{bmatrix} a_{0,0} & a_{0,1}& \dots & a_{0,n_1}\\ a_{0,1} & a_{1,1}& \dots & a_{1,n-1}\\ \vdots & \vdots& \ddots &\vdots\\ a_{k,0} & a_{k,0}& \dots & a_{k,n-1}\\ \vdots & \vdots& \ddots & \vdots\\ a_{n-1,0} & a_{n-1,1}& \dots & a_{n-1,n-1} \end{bmatrix} \]
グラフ構造のPythonでの実装
グラフ頂点の消滅生成イベントが発生した場合や、辺の追加・切断・付け替えが発生した場合など、動的にグラフを取り扱うためには隣接関係を再設定することが必要になる。 このような取り扱いを可能とするクラスとしてグラフを実装するには、このようなメソッド定義が必要になり、クラス設計自体が複雑になる。
ここでは、グラフを構成する頂点を与えて、その隣接関係を指定することによって静的にグラフ構造を表現する簡便な方法だけに留めよう。
有向グラフ

左図は順序付き有向グラフ(上図を再掲)を表している。 各頂点に添えられた赤い数字が、隣接する頂点間に導入された順番を示している。
次は8個の頂点 a, b, c, d, e, f, g, h に数字 0 から 7 を割り当て、辺に向きのある非順序有向グラフをPythonで oG0 と表したものである。
各頂点の隣接関係をPythonのリスト表現(記号 [ と ] で囲む)で表して順序付きとそ、その各隣接関係をリストにしてグラフを表している。
a, b, c, d, e, f, g, h = range(8) oG0= [ # Ordered digraph, node labels are numbers [b, c, d, e, f],#a [c, e], #b [d], #c [e], #d [f], #e [c, g, h], #f [f, h], #g [f, g] #h ]
次は同じ有向グラフ構造であるが、非順序グラフ G0 としてPythonで表したものである。 各頂点の隣接関係をPythonの集合(記号 { と } で囲む)で表し、各隣接関係をリストにしてグラフ G0を表している。
a, b, c, d, e, f, g, h = range(8)
G0= [ # UnOrdered digraph, node labels are numbers
{b, c, d, e, f},#a
{c, e}, #b
{d}, #c
{e}, #d
{f}, #e
{c, g, h}, #f
{f, h}, #g
{f, g} #h
]
無向グラフ

左図は辺に向きを付けない無向グラフ(上図を再掲)を表している。 各頂点に添えられた赤い数字が、隣接する頂点間に導入された順番を示している。
次は16個の頂点 a, b, c, d, e, f, g, h, i, j, k, l, m, n, o, p に数字 0 から 15 を割り当て、辺に向きのある順序付き有向グラフをPythonで oG1 と表したものである。
各頂点の隣接関係をPythonのリスト表現(記号 [ と ] で囲む)で表して順序付きとそ、その各隣接関係をリストにしてグラフ oG1 を表している。
a, b, c, d, e, f, g, h, i, j, k, l, m, n, o, p = range(16) oG1= [ # Ordered graph(undirected), node labels are numbers [b, e, f], #a [a, c, f], #b [b, d, g], #c [c, g, h], #d [a, f, i], #e [a, b, e, i], #f [c, d, j, k, l],#g [d, l], #h [e, f, j, m, n],#i [g, i, k], #j [g, j, n, o], #k [g, h, p], #l [i,n], #m [i, k, m], #n [k], #o [l] #p ]
次は同じ有向グラフ構造であるが、非順序グラフ G1 としてPythonで表したものである。 各頂点の隣接関係をPythonの集合(記号 { と } で囲む)で表し、各隣接関係をリストにしてグラフを表している。
a, b, c, d, e, f, g, h, i, j, k, l, m, n, o, p = range(16)
G1= [ # UnOrdered graph(undirected), node labels are numbers
{b, e, f}, #a
{a, c, f}, #b
{b, d, g}, #c
{c, g, h}, #d
{a, f, i}, #e
{a, b, e, i}, #f
{c, d, j, k, l},#g
{d, l}, #h
{e, f, j, m, n},#i
{g, i, k}, #j
{g, j, n, o}, #k
{g, h, p}, #l
{i,n}, #m
{i, k, m}, #n
{k}, #o
{l} #p
]
深さ優先探索
与えられたグラフ Gの頂点を set_univisited(G) によって、頂点属性を True として Unvisited に設定して「非訪問」リストを返す関数 set_univisited(G) である。
def set_univisited(G):
vstates = []
for vertex in range(len(oG1)):
vstates.append(None)
return vstates
次は、上の関数 set_univisited(G) を実施した結果を states として、与えられたグラフ Gの頂点 start から深さ優先探索(Depth First Search)して、訪れた頂点を出力する関数 DFS(G, start) である。
states = set_univisited(G)
def DFS(G, start):
states[start] = True
print start,
for u in G[start]:
if not states[u]:
DFS(G, u)
他の考え方による深さ優先探索
同じ結果をもたらす、別の深さ優先探索の関数を考えることができる。
与えられたグラフ Gの頂点 start から深さ優先探索(Depth First Search)して、訪れた頂点を出力する関数 DFS1(G, start, Visited=None) である。
def DFS1(G, start, Visited=None):
if Visited is None:
Visited = set()
Visited.add(start)
print start,
for u in G[start]:
if u in Visited:
continue # next for loop
DFS1(G, u, Visited)
有向グラフの場合、出発点によってはグラフの全ての頂点を訪れることができないことがある。 たとえば、上の順序付き有向グラフ oG0 を 頂点 g から深さ優先探索すると \[ oG_0: g\rightarrow f\rightarrow c\rightarrow d\rightarrow e\rightarrow h\quad \text{(finished)} \] となり、頂点 a には到達しない。
グラフの連結性(connectedness)などを調べるアルゴリズムが必要な所以である。
横幅優先探索
次は与えられたグラフ G(無向グラフでも有向グラフでもよい)の指定された頂点 srat から横幅優先探索(Breadth First Search)して、訪れた頂点を出力する関数 DFS(G, start, Visited=None) である。 データ操作 dequeue を使うために、Python標準ライブラリの collections をインポートしている。
import collections# for using dequeue
def BFS(G, s):
Visited= {s: None} # visited set of child:parent, edge from parent to child
UnVisited = collections.deque([s]) # list of unvisited nodes
while UnVisited:
u = UnVisited.popleft()
print u, # vising now
for v in G[u]:
if not(v in Visited):
UnVisited.append(v)
Visited[v] = u # v can be reached from u
return Visited
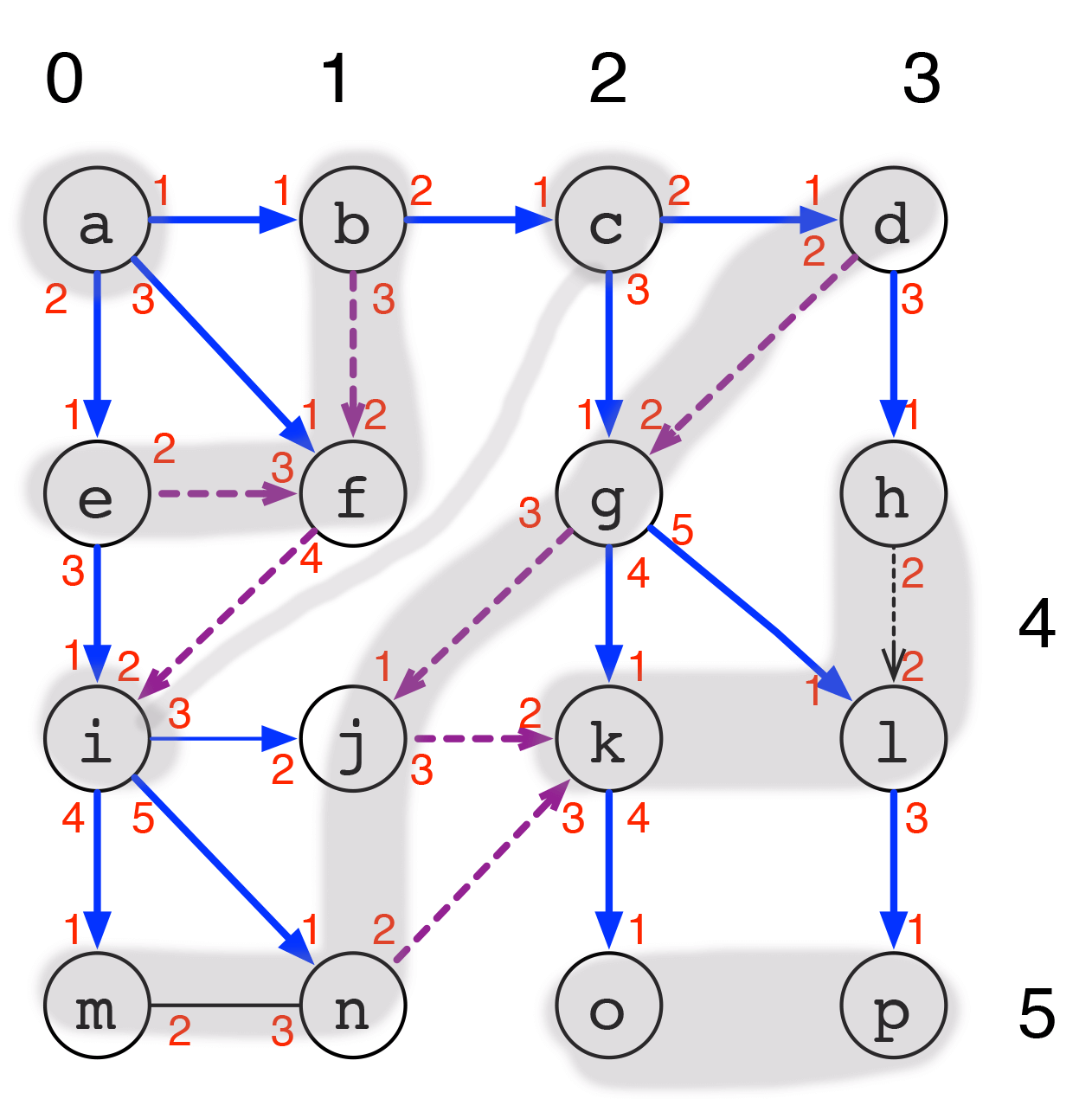 左図は上の順序付き有向グラフを oG1 を横幅優先探索した様子である。
頂点 a から探索を始めると、次のようになる(from "Data Structures and Algorithms in Python",Goodrich,Tamassia and Goldwasser, Wiley 2013)。
\[
oG1: a\rightarrow b\rightarrow e\rightarrow f\rightarrow c\rightarrow i\rightarrow d\rightarrow g\rightarrow j\rightarrow m\rightarrow n\rightarrow h\rightarrow k\rightarrow l\rightarrow o\rightarrow p \quad \text{(finished)}
\]
左図は上の順序付き有向グラフを oG1 を横幅優先探索した様子である。
頂点 a から探索を始めると、次のようになる(from "Data Structures and Algorithms in Python",Goodrich,Tamassia and Goldwasser, Wiley 2013)。
\[
oG1: a\rightarrow b\rightarrow e\rightarrow f\rightarrow c\rightarrow i\rightarrow d\rightarrow g\rightarrow j\rightarrow m\rightarrow n\rightarrow h\rightarrow k\rightarrow l\rightarrow o\rightarrow p \quad \text{(finished)}
\]
隣接関係に順序が付いていることによって、この結果になること理解しよう。
