Webページでは数式を表すためにLaTeX表記が使えるMathJaxを利用しています。 WebブラウザにはSafari/Chrome/Firefoxを使って下さい（IEでは表示できないようです。）

二分木（binary tree）クラスとその利用

データ構造としての木は多くのアルゴリズムにおいて中心的な考え方を提供する。特に、木は階層的構造を表現するのに都合が良い。

木構造の再帰的定義

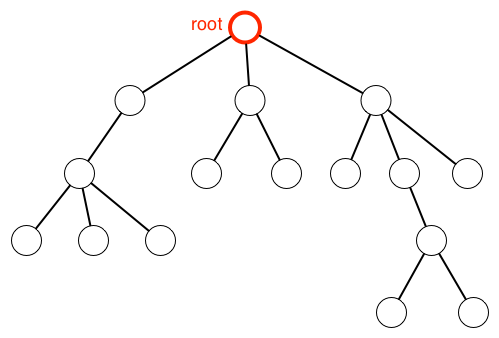
グラフ（graph）$G=(V, E)$ とは、頂点（vertex)または節（node）の集合 $V=(v_1,v_2,\dots, v_n)$ がそれぞれ辺（edge/arc）$e_{ij}$ で結ばれるという辺の集合 $E$ で特徴付けられる。木（tree）とは、左図のように閉路（closed path）のない連結なグラフである。木の各頂点は（閉路を形成しないように）複数の頂点に枝分かれして、元の頂点を親（parent）といいう、親から枝分かれした頂点を子（child）という。子を持たない頂点を葉（leaf）という。

これらの頂点の祖先（ancester）を特別に根（root）という。根からある頂点に到達する経路（1通りしかない）で渡る辺の数を頂点の深さ（depth）、その最大値を木の高さ（height）という。特に、以下で考えるように、子の並び方に順序がある木を順序付き木（ordered tree）という。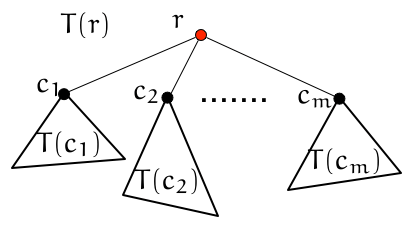

木の構成からわかるように、木 $T$ は次のように再帰的に定義される。

1つの頂点 $r$ からなるグラフは $r$ をルートとする木 $T$ である。
ルート $r$ とする木 $T(r)$ は、$r$ からその子への頂点 $c_1,\dots,c_m$ への辺を取り除いて得られる $c_1,\dots,c_m$ をルートとする部分木 $T(c_1),\dots,T(c_m)$ に分割される。
辺を取り除く操作を回復させて（記法 $\oplus$ で表すとしよう）形式的に書くと \[ T(r)=\{r\} \oplus T(c_1) \oplus \dots \oplus T(c_m) \]

2分木 binary tree

木の枝分かれ、つまり、親頂点の子の数が2であるような木を二分木（binary tree）という。 $r$ をルートとする二分木 $T(r)$ は、ルートだけからなる部分木 $\{r\}$ と（$r$ からの辺を取り除いて得られる） $r$ に関する左部分木 $T_{L(r)}$ および右部分木 $T_{R(r)}$ に分割される。
辺を取り除く操作を回復させて（記法 $\oplus$ で表すとしよう）形式的に書くと \[ T(r) = \{r\} \oplus T_{L(r)} \oplus T_{R(r)} \] である。

二分木をリストで表す関数

次の関数定義では、二分木 r の生成 binary_tree(r)、ルート値の設定 put_root(root, new_val)、左部分木への要素挿入 insert_left(root, new_branch)、右部分木への要素挿入 insert_right(root, new_branch)、ルート値の取得 get_root(root)、左部分着の取得 get_left(root)、左部分着の取得 get_right(root) を定義した。

def binary_tree(r = None):
    return [r, [], []]

def put_root(root, new_val):
    root[0] = new_val

def insert_left(root, new_branch):
    t = root.pop(1)
    if len(t) > 1:
        root.insert(1, [new_branch, t, []])
    else:
        root.insert(1, [new_branch, [], []])
    return root

def insert_right(root, new_branch):
    t = root.pop(2)
    if len(t) > 1:
        root.insert(2, [new_branch, [], t])
    else:
        root.insert(2, [new_branch, [], []])
    return root

def get_root(root):
    return root[0]

def get_left(root):
    return root[1]

def get_right(root):
    return root[2]

演習：この関数定義をつかって、次を実行するスクリプト binary_list_tree.py を書いて実行しなさい。

r = binary_tree()
print r
put_root(r, 3)
print r
insert_left(r, 4)
print r
insert_right(r, 6)
print r
insert_right(r, 7)
print r
insert_left(r, 5)
print r
left = get_left(r)
print left
print(get_root(left))
right = get_right(r)
print right 
print get_root(right)

実行結果は次のようになる。

$ ./binary_list_tree.py
[None, [], []]
[3, [], []]
[3, [4, [], []], []]
[3, [4, [], []], [6, [], []]]
[3, [4, [], []], [7, [], [6, [], []]]]
[3, [5, [4, [], []], []], [7, [], [6, [], []]]]
[5, [4, [], []], []]
5
[7, [], [6, [], []]]
7

二分木を表すクラス binarytree

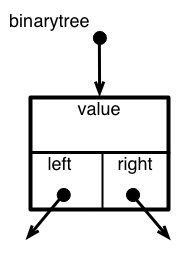
上のように、二分木をリストを使って表すと、括弧 [ と ] に埋もれてしまう。そこで、次のようにして二分木を表すクラス binarytree を定義しよう。インスタンスの生成は binarytree(a) だが、引数を取らない場合にはルートの値を持たない（None）空ツリーを生成する。

クラス binarytree は二分木の頂点 node の内部構造を与えている。 node.value のノードの値を保持、node.left および node.right は他の二分木の頂点を指し示すポインタが格納される（インスタンスとして生成されたとき（二分木の葉に相当）には、何も指し示していないので None に初期化されている。

その状況をよく示すのは、二分木の左右に新たに値 insert を持つノードを挿入するメソッド insert_left(insert) および insert_right(insert) である。

class binarytree:
    def __init__(self, root = None):
        self.value = root
        self.left = None
        self.right = None

    def insert_left(self, insert):
        if self.left == None:
            self.left = binarytree(insert)
        else:
            t = BinaryTree(insert)
            t.left = self.left
            self.left = t

    def insert_right(self, insert):
        if self.right == None:
            self.right = binarytree(insert)
        else:
            t = binarytree(insert)
            t.right = self.right
            self.right = t

    def get_right(self):
        return self.right

    def get_left(self):
        return self.left

    def put_root(self, obj):
        self.value = obj

    def get_root(self):
        return self.value

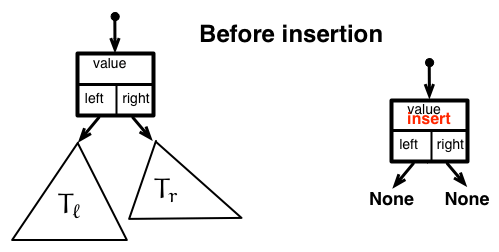
二分木の左部分木への要素挿入のメソッド insert_left(self, insert) と右部分木への要素挿入のメソッド insert_right(root, insert) に注目しよう。インサートしたい値 insert を指定してインスタンス binarytree(insert) を生成する（左図の右）。二分木のleft が self.left == None （何もポイントしていない）なら、self.left = binarytree(insert) によって left がインスタンスをポイントさせるようにしている。

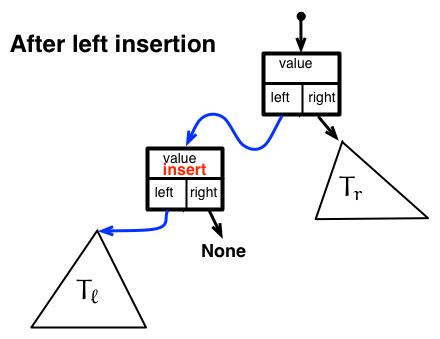
一方、二分木のleft が左部分木を持てば（右図）、インスタンス t = BinaryTree(insert) の left に左部分木をポイントさせるために t.left = self.left とし、さらに、右部分木として left がインスタンス t を指すように self.left = t とするのである。

演習：上のスクリプト binary_list_tree.py をクラス binarrytree を使って書き直したスクリプト binary_tree.py を実行してみなさい。

二項演算式の二分木表現

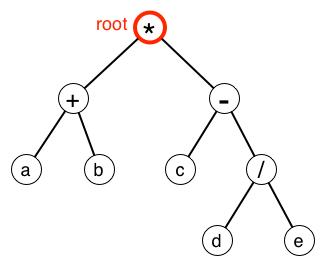
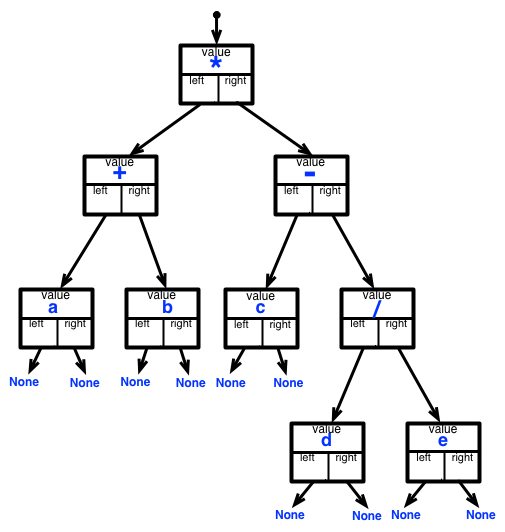
2項 $a, b$ の演算 $a\odot b$ は、演算子 $\odot$をルートに $a$を左側の子、 $b$を右側の子として二分木で表されることに注意すると、二項演算子を1つ以上含む計算式は二分木で表されることを示すことができる。この二分木には、葉以外の頂点には演算子が、葉にはオペランドが配置されている（一般に、$a\odot b\not= b\odot a$ であるために、二分木は順序月である必要があることに注意しよう）。右図は (a + b) * (c - d / e) の二分木表現である。

二項演算式の二分木表現において、ルートとなる記号はどのように決定されるかを考えてみなさい。

演習：左図（クリックして拡大）のように、上の (a + b) * (c - d / e) の二分木表現をクラス binarytree を使って表現してみなさい。

二分木の探索

グラフ $G=(V, E)$ において、$n$個かならる頂点 $V=\{v_1, v_2,\dots, v_n\}$ を何らかの方法で1回だけ訪れること \[ \text{Search of $G$}= v_{\tau(1)},v_{\tau(2)},\dots ,v_{\tau(n)} \] を$G$の探索（search）または走査（traversal）という。ここで $\tau$ は $(1,2,\dots, n)$ の並べ替え（permutaion）である。 $n$個の頂点を持つグラフの探索は $n!$ 通りある。

与えられたグラフ $G$ をそのグラフ構造を反映していかにして効率的に探索するかは、人工知能をはじめとする多くの戦略的アルゴリズムにおける中心的課題の一つである。

二分木の構造を活かした探索は次の3つがある。

前順探索（pre-order search）：ルートを訪れ、左部分木を探索、右部分木を探索する。
中順探索（in-order search）：左部分木を探索、ルートを訪れ、右部分木を探索する。
後順探索（post-order search）：左部分木を探索、右部分木を探索して、ルートを訪れる。

スタックの応用(承前)では、2項演算子からなる計算式を括弧 ( と ) を使わずに、後置き記法(逆ポーランド記法)で表式を表すことができた。これは偶然のことではなく、二項演算子の二分木表現の探索として考えると次の対応にあることが分かる。

前順探索 $\Leftrightarrow$ 前置き記法（prefix notation）
中順探索$\Leftrightarrow$ 中置き記法（infix notation）
後順探索$\Leftrightarrow$ 後置き記法（postfix notation）

次は、binarytreeクラスの二分木インスタンス btree を後順探索するグローバル関数 post_order_serach(btree) の定義である（Python2で書いている。記号を改行しないように、カンマ(,)をつけて print している）。

def post_order_serach(btree):
    if btree != None:
        post_order_serach(btree.get_left())
        post_order_serach(btree.get_right())
        print btree.get_root(),

グローバル関数 post_order_serach の使い方は次のようになる。

bt = binarytree()
...
   インスタンス bt を生成してから目的の二分木 btree を得るプロセス
...
post_order_serach(bt) # br の頂点を後順探索で書き出す

探索のメソッド化

一方、binarytree クラスのメソッドとして二分木を後順探索するように上のクローバル関数 post_order_serach を書き換えるには次にように書く。クラス内のメソッドであるので、引数に self が必要であること以外に、5,7行目で左部分木 self.left および右部分木 self.right が存在することを確認して　から、それぞれの部分木にメソッド post_order_serach() を適用していること、その後に9行目でルート値 self.value を書き出していることに注意しよう。（ここでも、Python2で書いている。記号を改行しないように、カンマ(,)をつけて print している。）

# inside definition of class binarytree

    def post_order_serach(self):
        if self != None:
            if self.left:
                self.left.post_order_serach()
            if self.right:
                self.right.post_order_serach()
            print self.value,

クラス binarytree 内のメソッドとして定義した post_order_serach を使うには次のようにする。

bt = binarytree()
...
   インスタンス bt を生成してから目的の二分木 btree を得るプロセス
...
bt.post_order_serach() # br の頂点を後順探索で書き出す

二項演算式の二分木表現 btree に対して、post_serach_binarytree(btree) が後置き記法を与えることを確かめるスクリプト post_serach.py を書いて実行しなさい（たとえば、(a + b) * (c - d / e) の二分木表現を使う）。