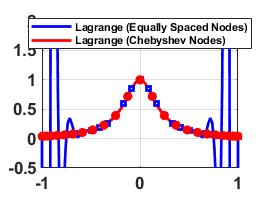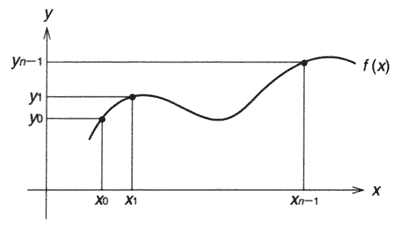

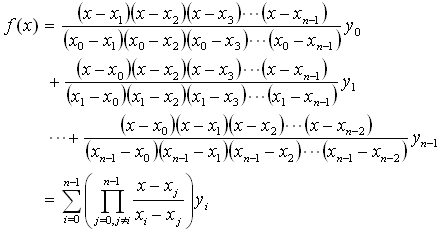
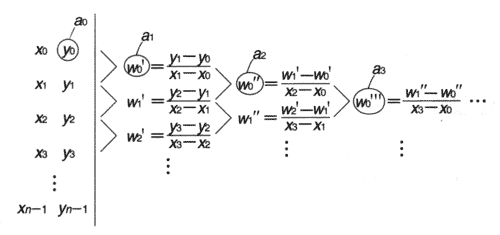
double x[3] = {0, 4, 8};
double y[3] = {1.2, -2.3, 6.4};
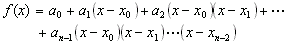
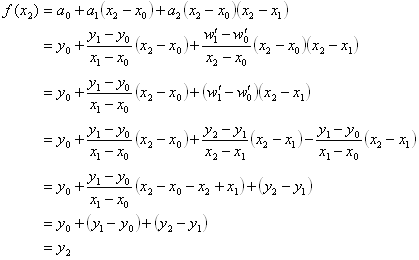
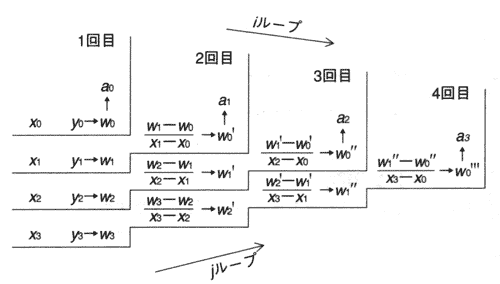
Z:\compmech\ex8> 8_1.exe data2.txt Num of data: 9 x = -19.6085, y = -24.061475 (Lagrange), y = -24.061475 (Newton) … x = 4.3000, y = 1.500000 (Lagrange), y = 1.500000 (Newton)
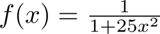

Z:\compmech\ex8> 8_2.exe output.csv Interpolation results saved to output.csv