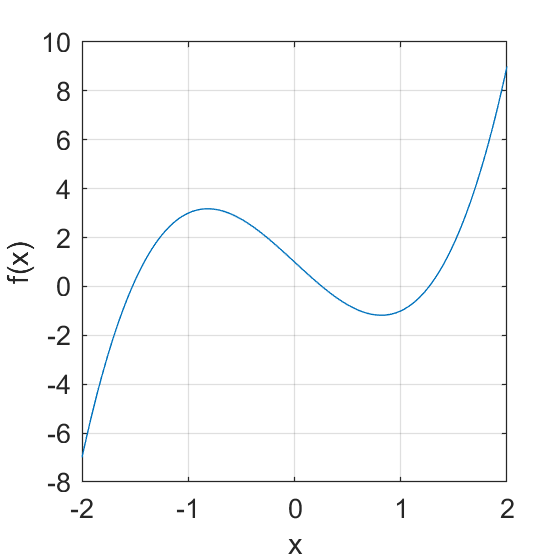
図 解くべき方程式の把握
double func(double x) {
return( 2*x*x*x - 4*x + 1 );
}
ここでは、対象とする区間を、a = -2, b = 2として考える。このとき、値の推移をなるべく細かく把握できるよう、この区間を n=100 分割して値を表示することにする。
#include<stdio.h>
double func(double x) { ... (上に書いてあるので、省略)
int main(void) {
const double a = -2.0;
const double b = 2.0;
const int n = 100;
for(int i=0; i<=n; i++) { ...
(以降の処理を考えてください)
以下のような出力結果が得られるよう、上のプログラムの続きを作成せよ。
x = -2.000, f(x) = -7.000 x = -1.960, f(x) = -6.219 x = -1.920, f(x) = -5.476 ... x = 1.960, f(x) = 8.219 x = 2.000, f(x) = 9.000
z:\compmech\ex04> func_test.exe > data.txtこれらの値を利用すると、Excelなどを利用して下図のようにグラフの形状を確認することもできる。 f(x) = 0 を満たす解は、区間[-2 -1], [0 1], [1 2]に存在することがわかる。

#include<stdio.h>
typedef double fp(double); //関数ポインタ
double func(double x) {
return( 2*x*x*x - 4*x + 1 );
}
double func2(double x) {
return( 4*x*x*x - 3*x*x + 2*x + 1 );
}
void show_func(fp* func, const double a, const double b, const int n) {
for(int i=0; i<=n; i++) { ...
(5.1と同じ処理を記述)
}
}
int main(void) {
show_func(func, -2, 2, 100);
show_func(func2, -2, 2, 100);
return 0;
}
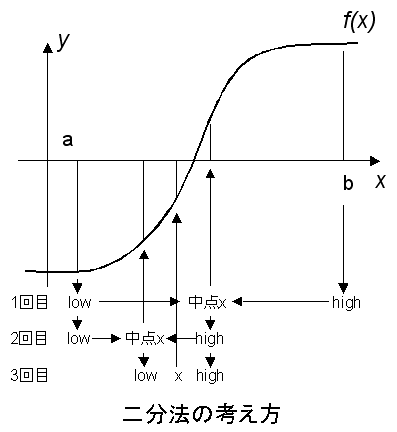
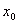 を初期値とする.
を初期値とする.
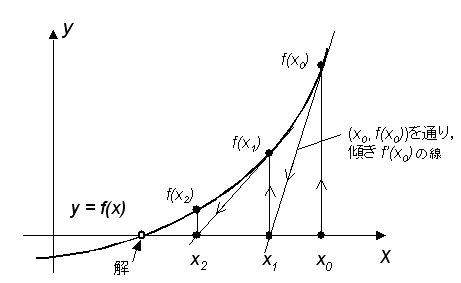
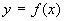 の
の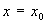 における接線を引き,
における接線を引き,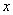 軸と交わったところを
軸と交わったところを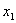 とし,以下同様の手順で
とし,以下同様の手順で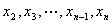 と求めていく.
と求めていく.
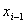 から
から 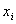 を求める方法は、点
を求める方法は、点 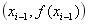 、傾き
、傾き 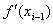 の直線の方程式を考えることにより
の直線の方程式を考えることにより
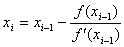
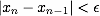 になったときの
になったときの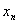 の値を求める解とする.そうでなければ2.以降を繰り返す.
の値を求める解とする.そうでなければ2.以降を繰り返す.
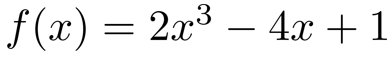
// 関数f(x)の微分式
double dfunc(double x)
{
return /* 求める関数の導関数 */ ;
}
Z:\compmech\ch05>5_1.exe 0.12 0.45 0.78 ----- Answers ‘f(x) = 0.0’ ----- x[1] = 1.234 (initial value: 0.12 --> iteration: 3 times) x[2] = 5.678 (initial value: 0.45 --> iteration: 6 times) x[3] = 9.012 (initial value: 0.78 --> iteration: 9 times)
Z:\compmech\ch05>5_2.exe 1.2 3.4 1.2 ----- Answers ‘x = 1.5’ ----- < Bisection Method > theta = 1.234 rad (low: 1.2, high: 3.4 --> iteration: 56 times) < Newton Method > theta = 1.234 rad (initial value: 1.2 --> iteration: 3 times)