Webページでは数式を表すためにLaTeX表記が使えるMathJaxを利用しています。 WebブラウザにはSafari/Chrome/Firefoxを使って下さい（IEでは表示できないようです。）

自由度2の力学 Henon-Heiles系

Hamiltonの正準方程式

解析力学の教えるところによると、Lagrangian $L(\boldsymbol{q},\dot{\boldsymbol{q}},t)$ が与えられたとき、運動方程式はEuler-Lagrange方程式 \[ \frac{d}{dt}\left(\frac{\partial L}{\partial \dot{q_i}}\right)-\frac{\partial L}{\partial q_i}=0,\qquad i=1,\dots, n \] で与えられる。

いま、$q_i$ に共役な運動量 $p_i$ を \[ p_i =\frac{\partial L}{\partial\dot{q_i}},\qquad i=1,\dots, n \] で定義する。 もし、$\dot{q_i}$ が $q_1,\dots,q_n$ および $p_1,\dots,p_n$ の関数 $\dot{q_i}=\dots{q_i}(\boldsymbol{q},\boldsymbol{p})$ と解くことができる、つまり、次の関数行列式が非零 \[ \left\vert \frac{\partial^2 L}{\partial\dot{q_i}\partial\dot{q_k}} \right\vert \not=0 \] のとき、Legendre変換によって得られる関数 \[ H=\sum_{i=1}^n \dot{q_k}p_k -L(\boldsymbol{q},\dot{\boldsymbol{q}},t) \] は $q_1,\dots,q_n$ および $p_1,\dots,p_n$ の関数 $H(\boldsymbol{q},\boldsymbol{p}, t)$ となる。 $H$ を Hamiltonian という。

Hamiltonian $H(q_1,\dots q_n, p_1,\dots ,p_n, t)$ が与えらたとき、位置 $q_i$ と運動量 $p_i$ に関する運動方程式を正準方程式（canonial eqs. of motion）といい、次で与えられる。 \begin{align*} \frac{d}{dt}q_i &=\frac{\partial H}{\partial p_i},\\ \frac{d}{dt}p_i &=-\frac{\partial H}{\partial q_i}. \end{align*}

正準方程式の数値計算

ポテンシャル関数 $U(q_1,\dots ,q_n)$ をもつHamiltonian $\displaystyle H(q, p)=\sum_{i=1}^n \frac{1}{2m_i}p_i^2 +U(q_1,\dots ,q_n)$ の正準方程式 \begin{align*} \frac{d}{dt}q_i &= \frac{p_i}{m_i},\\ \frac{d}{dt}p_i &= -\frac{\partial U}{\partial q_i}\equiv f(q_1,\dots ,q_n) \end{align*} を差分化して運動方程式を数値計算してみよう。 すなわち、差分刻み$\Delta t$と初期値$\boldsymbol{q}^{(0)}=(q_1^{(0)},\dots ,q_n^{(0)})$, $\boldsymbol{p}^{(0)}=(p_1^{(0)},\dots ,p_n^{(0)})$のもとで時刻 $t_j=j\Delta t$ における数値解 $\boldsymbol{q}(t_j)=\boldsymbol{q}^{(j)}$, $\boldsymbol{p}(t_j)=\boldsymbol{p}^{(j)}$を求める。

微分方程式の数値解法で触れたように、計算精度の向上にはRunge-Kutta法（さらにはその改良版）など多くの研究がある。 Henon-HeilesはRunge-Kutta法を使った（[論文]75ページ左下段）。 ここでは、正準方程式というHamilton系の特性である同時刻交換関係を保つように考案したV. Moncrief がFinite-difference approach to solving operator equations of motion in quantum theory（Phys. Rev. D 28, 2485）で提案した差分スキームを使ってみよう。

Moncriefは次のような差分方程式が有効であることを示した（論文の式(5)）。 $f_k(\boldsymbol{q}^{(j)})=\displaystyle-\frac{\partial U(\boldsymbol{q})}{\partial q_k}$として \begin{align} q_k^{(j+1)} &= q_k^{(j)} + \frac{\Delta t}{m_k} \left( p_k^{(j)} +\frac{\Delta t}{2} f_k(\boldsymbol{q}^{(j)}) \right),\\ p_k^{(j+1)} &=p_k^{(j)} +\frac{\Delta t}{2} \left(f_k(\boldsymbol{q}^{(j)})+f_k(\boldsymbol{q}^{(j+1)}) \right). \end{align}

Henon-Heiles系

Henon-Heilesは 1964年にThe applicability of the third integral of motion: Some numerical experiments（he Astrophysical Journal 69: 73–79）において、次の自由度2のHamitonianの数値的研究を行った。 \[ H(x,y,p_x,p_y)=\frac{1}{2}(p_x^2+p_y^2)+\frac{1}{2}(x^2+y^2)+x^2y-\frac{1}{3}y^3 \]

解くべき運動方程式は次のようになる。 \begin{align} \dot{x}&=p_x\\ \dot{y}&=p_y\\ \dot{p_x}&=-x-2xy\\ \dot{p_y}&=-y-x^2+y^2 \end{align}

初期条件

先の演習で確かめたように、時間の恒量である全エネルギー値 $E$ は Hamiltonian $H$ の関数値から定まり、 運動の軌道は4次元の相空間内の集合 \[ \left\{ (x,y,p_x,p_y) \,\vert\, E=\frac{1}{2}(p_{x}^2+p_{y}^2)+\frac{1}{2}(x^2+y^2)+x^2y-\frac{1}{3}y^3 \right\} \] で定まる3次元超平面上にある。 $E$ の値によっては運動は有界範囲で生じるとは限らないことを後で見る。

Henon-Heilesは運動の様子を見るために $x=0$ で、しかも $x$ 方向の速度が正、つまり運動量$p_x$が負値から $p_x=0$を通過して $p_x>0$ であるように軌道が $(y,p_y)$ 平面を横切る点列 $P_1,P_2,\dots$ としてプロットした（[論文]Fig.3、式(9)）。 このとき 横断面 $(y,p_y)$ 上の点　$P_m\rightarrow P_{m+1}$ はPoincare写像を与える。

系の 全エネルギー $E$ は初期値 $(x_0=0,y_0,p_{x0},p_{y0})$ で与えられ、初期値 $p_{x0}$ は式 \begin{equation} p_{x0}=\sqrt{2E-p_{y0}^2-y_0^2+\frac23 y_{0}^3} \end{equation} を満たすように取ればよい。

ポテンシャル関数と停留点判別式

偏微分可能な2変数関数 $f(x,y)$ において、 \[ \frac{\partial f}{\partial x}(a,b)=\frac{\partial f}{\partial y}(a,b)=0 \] であるような点 $(a,b)$を停留点（または臨界点）という。

[定理] $C^2$級の2変数関数 $f(x,y)$の停留点 $(a,b)$ において、次が成り立つ。 \[ f_{xx}(a,b)=\frac{\partial^2 f}{\partial x^2}(a,b),\quad f_{xy}(a,b)=\frac{\partial^2 f}{\partial x\partial y}(a,b),\quad f_{xx}(a,b)=\frac{\partial^2 f}{\partial y^2}(a,b) \] としたときの判別式 $(a,b)$ \[ D(a,b)=f_{xx}(a,b)f_{yy}(a,b)-f_{xy}^2(a,b) \] において、 \begin{align*} D(a,b)>0 \quad\text{and}\quad f_{x}(a,b) >0\quad & \text{$(a,b)$ は極小}\\ D(a,b)>0 \quad\text{and}\quad f_{x}(a,b) <0\quad & \text{$(a,b)$ は極大}\\ D(a,b) < 0\quad & \text{$(a,b)$ は鞍点（双曲点）}\\ D(a,b) =0\quad & \text{$(a,b)$ の極値の判定不能}\\ \end{align*}

Henon-Heiles系のポテンシャル関数 $U(x,y)=\displaystyle\frac{1}{2}(x^2+y^2)+x^2y-\frac{1}{3}y^3$の性質を調べておこう。 停留点$ (x_0,y_0)$ は \[ (0,0),\quad (0,1), \quad \left(\frac{\sqrt{3}}{2},-\frac12\right),\quad \left(-\frac{\sqrt{3}}{2},-\frac12\right) \] であり \[ U_{xx}=\frac12 (2+4y),\quad U_{xy}=2x,\quad U_{yy}=\frac12 (2-4y) \] より、$(0,0)$ だけが極小で、ほかの3点は鞍点である。

演習：

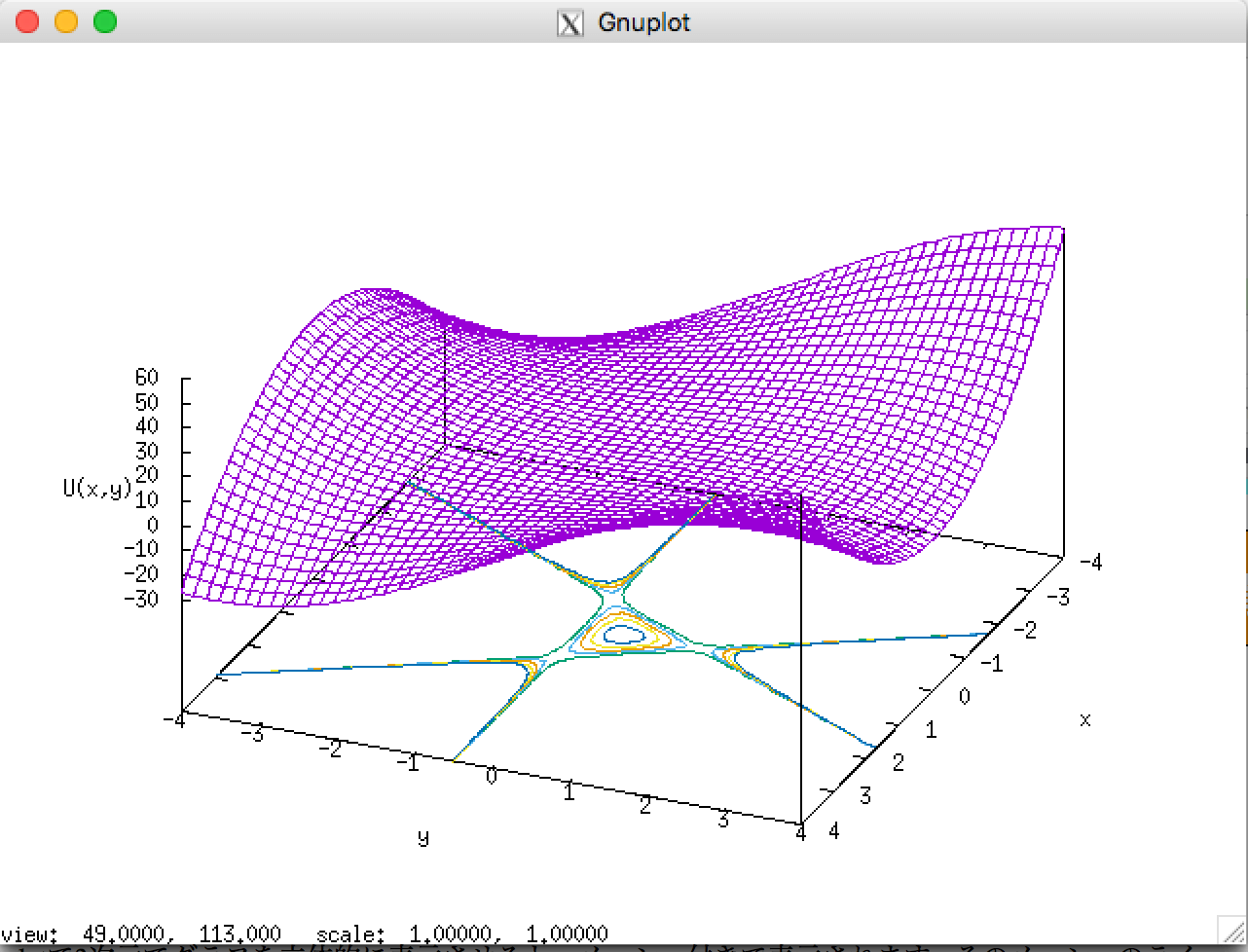
左図（クリックで拡大）は、Henon-Heiles系のポテンシャル関数 $U(x,y)$ の様子とその等高線である。 このような図を Gnuplotで描いてみなさい。
（ヒント）： set isosamples, set contour, set cntrparam levels incremental, set nokey などを使った設定をしてから splot u(x,y) する。

有界運動となる全エネルギー

運動方程式をベクトル場とする不動点（$(\dot{x},\dot{y},\dot{p_x},\dot{p_y})=(0,0,0,0)$となる点集合）を考えよう。 式(3)(4)より、$p_x=p_y=0$ であって、全エネルギー $E$ は $E=\frac{1}{2}(x^2+y^2)+x^2y-\frac{1}{3}y^3$ となっている。 このとき式(5)からは $x(1+2y)=0$、(5)からは $-x^2=y(1+y)$ の関係にあることより これより \begin{gather*} x=0 \quad \text{and} \quad y=1, -1\\ \text{or}\\ x\not= 0 \quad \text{and} \quad y=-\frac{1}{2} \end{gather*} を満たす。

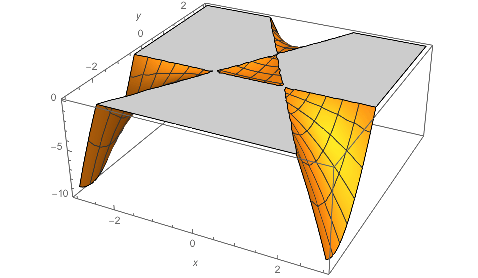
従って、$(0,1), (\sqrt{3}/2,-1/2), (-\sqrt{3}/2,-1/2)$ はポテンシャルの停留鞍点で、これらを結ぶ正三角形上にある点は不動点でもある。 その全エネルギー値は $E=\displaystyle\frac16$ である。 したがって、$E> 1/6$ を越えるエネルギーでは、左図（クリックで拡大）のポテンシャル値 $1/6 での断面から示唆されるように、この双曲不動点から近傍から無限遠へ遠ざかる軌道が存在することになる。

以上のことから、Henon-Heiles系の全運動エネルギーは $E < 1/6=0.1666\dots$ であるようにして、初期条件 $(x_0=0,y_0,p_{x0},p_{y0})$ を選んで数値計算を行うことにする。

Henon-Heiles系の数値計算

次は、式(1), (2) で与えらるMoncriefの方法によるHamiltonの運動方程式の差分化 moncrief(z0, dt, force) である。 引数 z0 で座標の組 q0$=(x_0,y_0,\dots)$ と運動量 p0$=(p_{x0}, p_{y0},\dots)$ からなるリスト z0$=(x_0,y_0,\dots, p_{x0}, p_{y0},\dots) $ を与えたときの時間刻み dt$=\Delta t$ 後のリスト $(x_1,y_1,\dots, p_{x1}, p_{y1},\dots) $ を返す。 各運動量成分に働く力関数のリストは force で与えられるとしている。

# Moncrief didderence method for force after a time step dt
def moncrief(z0, dt, force):
    # z0 = [x0, y0, ..., px0, py0, ...] list of initial positions and  momentums
    # time step
    # list of force functions
    width = len(z0) / 2# degrees of freedom
    t = 0
    q = z0[0:width]
    p = z0[width:]
    z1 = []# [x1, y1,.., px1, py1...]
    f0 = map(lambda a: a(*q), force)
    for i in range(width):
        q[i] += dt * (p[i] + dt / 2.0 * f0[i])
    z1.extend(q)
    f1 = map(lambda a: a(*q), force)
    for i in range(width):
        p[i] += dt / 2.0 * (f0[i] + f1[i])
    z1.extend(p)
    return z1

次は、 24行目の q0$=(x_0,y_0)$ および 26行目で p0$=(p_{x0}, p_{y0})$ で初期卯条件を与え、時間刻み dt$=\delta t =0.01$ 、時間刻み dt$=\Delta t$ を使って、経過時間 $T=300$ にわたる軌道 orbit を計算している。 ただし式(7) にあるように、10行目では、$x=0$ および全エネルギ- $e$ としたとき$y$座標値の初期値 $y_0=$y および$y$-運動量の初期値 $p_{y0}=$py から$x$-運動量の初期値 $p_{x0}$を求める関数 give_px(e, y, py) を定義している。 これを使って 25行目で初期値 px$ を決めている。

時間刻み dt 後の軌道成分をMoncriefの方法を使って求めるために、引数として与える初期値の組 z0 を用意するために、30行目で 空リスト [ ] を定義し、31行目で座標要素を追加して [x0,y0]、32行目で運動量要素を追加して [x0,y0,px0,py0] としている。 また、軌道成分を格納する空リスト orbit を33行目で用意して、34行目で初期軌道要素を追加していることに注意しよう。35行目から38行目でMoncriefの方法をくり返し適用して時間経過 T に渡る軌道成分を orbit に追加している。

import Gnuplot # Gnuplot.py がインストールされているとき
import math

# force functions(right hands of dpx/dt, dpy/dt) of Henon-heiles system
def fx(x, y):
    return -x - 2.0 * x * y
def fy(x, y):
    return -y - x**2 + y**2

# give a momentum px under the condion x=0 with given energy e
def give_px(e, y, py):
    return math.sqrt(2.0 * e - py**2 -y**2 + 2.0/3.0 * y**3)

# Total energy
def energy(x, y, px, py):
    return (px**2 + py**2) / 2.0 + (x**2 + y**2) / 2.0 + (x**2) * y  -  y**3 / 3.0


# force functions
henon_heiles = [fx, fy]

# data for calculation
e=0.165
q0 = [0.0, 0.0]# (x0,y0)
px = give_px(e, 0.0, 0.1)
p0 = [px, 0.1]# (px0, py0)
dt = 0.01#time step
T = 300# total time

z0 = []
z0.extend(q0)# forst part of list(positions)
z0.extend(p0)# second part of list(momentums)
orbit = []
orbit.append(z0)
for i in range( int(T/dt) ):
    z1 = moncrief(z0, dt, henon_heiles)
    z0 = z1
    orbit.append(z0)
#print orbit
for i in range(len(orbit)):
    print energy(orbit[i][0], orbit[i][1], orbit[i][2], orbit[i][3])

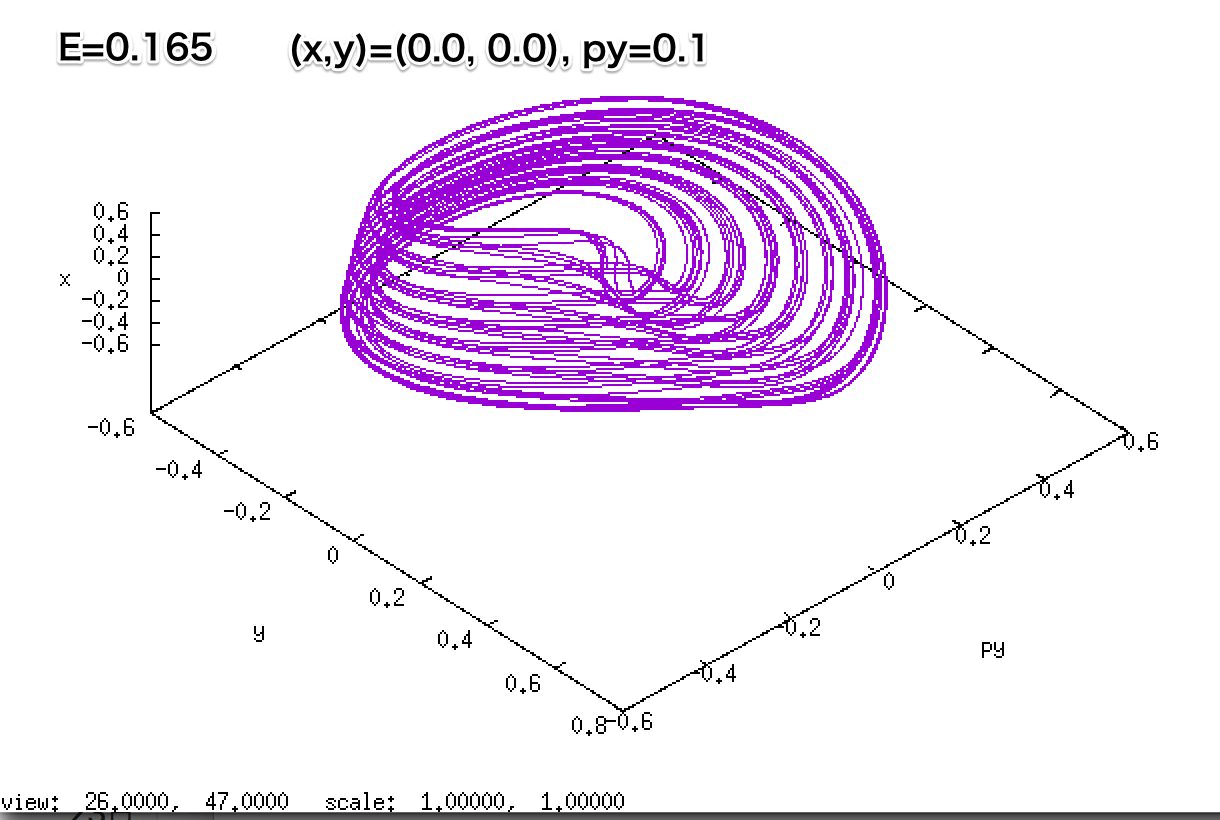
次は、Gnuplot.py がインポートできる環境下での軌道の様子をプロットするための追加スクリプトである。

xorbit = []
yorbit = []
zorbit = []
for i in range(len(orbit)):
    xorbit.append(orbit[i][1])
    yorbit.append(orbit[i][3])
    zorbit.append(orbit[i][0])
#print xorbit
#print yorbit
 
dat = Gnuplot.Data(xorbit, yorbit, zorbit)
gp = Gnuplot.Gnuplot()
gp('set terminal x11')
gp('set style data lines')
gp.set(xlabel="y",
 ylabel="py",zlabel="x")
gp.splot(dat)

Poincareの切断面の方法

軌道が平面 $x=0$ を $p_x$ であるような（$p_x$が増加する方向で平面 $x=0$ を横切る）平面 $x=0$ 上の点列 $(y_i,P_{y_1})$ を求めることによって軌道の様子を知る微分方程式の数値解法（Poincareの切断面の方法 surface of section）の方法を採用してみよう（Henon-Heiles[論文]の式(9)）。

数値軌道列 $\{(x_i,y_i,p_{x_i},p_{y_i})\}$ において、平面 $x=0$の点 $(y,p_y)$ が平面 $x=0$を「下からから上に」横断するとは、次のような条件を満たす集合 $(y_k,p_{y_k})$ だと考えることができる。 \[ \left\{ (y_k,p_{y_k}) \, \vert \, x_kx_{k+1} <0 \quad\text{and}\quad p_{x_k}>0\quad\text{and}\quad p_{x_{k+1}} >0 \right\} \]

Henon-Heilesの数値実験を再現する

Henon-HeilesのThe applicability of the third integral of motion: Some numerical experimentsにある、エネルギー値 E = 0.0833（Fig.4）、E = 0.125（Fig.5）および E = 0.16667（Fig.6）について、論文の図から $(y_0,p_{y_0})$ を読み取って、平面 x=0 を $p_x>0$ で横切る点列 $\{(y_i,p_{y_i})\}$ をプロットしてみよう。