Webページでは数式を表すためにLaTeX表記が使えるMathJaxを利用しています。 WebブラウザにはSafari/Chrome/Firefoxを使って下さい（IEでは表示できないようです。）

微分方程式の数値解法

$m$次元空間$M$内の解曲線 $\boldsymbol{x}(t)=(x_1(t),\dots,x_m(t))$ を初期条件 $\boldsymbol{x}(t_0)=(x_1(t_0),\dots,x_m(t_0))$ のもとで定める微分方程式系 \begin{align*} \frac{dx_1}{dt}&=v_1(\boldsymbol{x}, t), \quad x_1(t_0)=x_{10}\\ \vdots &\\ \frac{dx_m}{dt}&=v_m(\boldsymbol{x}, t), \quad x_m(t_0)=x_{m0} \end{align*} をベクトル表記して、次のように表す。 \[ \frac{d\boldsymbol{x}}{dt}=\boldsymbol{v}(\boldsymbol{x},t),\qquad \boldsymbol{x}(t_0)=\boldsymbol{x}_0 \] この微分方程式は各点 $\boldsymbol{x}$ および時間 $t$ 毎に各点で接線ベクトル $\boldsymbol{v}(\boldsymbol{x},t)\in \mathbb{R}^m$ を与えているとみることができ、$\boldsymbol{v}:M\rightarrow \mathbb{R}^m$ をベクトル場ということがある。

時間経過 $\Delta t$ 後にの $\boldsymbol{x}$ の変化$\Delta\boldsymbol{x}(t)=\boldsymbol{x}(t+\Delta t)-\boldsymbol{x}(t)$を考えると 関数$\boldsymbol{x}(t)$の微分操作とは \[ \frac{d\boldsymbol{x}}{dt}＝ \lim_{\Delta t\rightarrow 0}\frac{\boldsymbol{x}(t+\Delta t)-\boldsymbol{x}(t)}{\Delta t} \] の関係にある。 このことを素朴に考えると、有限ではあるが十分小さい時間変位 $\Delta t$ に対しては \[ \frac{\boldsymbol{x}(t+\Delta t)-\boldsymbol{x}(t)}{\Delta t}\approx \boldsymbol{v}(\boldsymbol{x}(t),t) \] が期待できる。 そこで時間刻み $\Delta t$ ごとに、$t$ をパラメータとする解曲線 $\boldsymbol{x}(t)$ に近いと考えられる離散的な値を逐次求める微分方程式の数値解法がさまざまに考案されてきた。

時刻$t=t_0$における初期条件$\boldsymbol{x}(t_0)$から逐次的に求めて得られる点列を$\{\boldsymbol{x}_n\}(n=0,1,2,\dots)$と表記する（$\boldsymbol{x}_0=\boldsymbol{x}(t_0)$）。 以下では、簡単のために時間刻みを $\Delta t$ を一定とする。

Euler法

Euler法とは、 点列 $\boldsymbol{x}_0, \boldsymbol{x}_1,\dots, \boldsymbol{x}_n,\dots$ を次のようにして逐次的に求める方法である。

\[ \boldsymbol{x}_{n+1}= \boldsymbol{x}_n +\Delta t\cdot \boldsymbol{v}(\boldsymbol{x}_n, t_n),\quad t_n = t_0 + n\Delta t,\quad n\geqq 0. \]

次で定義したPython関数 euler_orbit(x0, T, dt, vectorfield) は、Euler法を使って解軌道の数値リストを求めている。 vectorfield はベクトル場 $\boldsymbol{v}$ を定める $m$ 個の関数名のリスト [$v_1$, $\dots$, $v_m$] である。 時刻 $t_0$ における$m$次元（2行目の width に次元の値が格納される）の初期点リスト x0 =[$x_{01}$,$\dots$,$x_{0m}$]から出発して、時刻 $t_0$ から $t_0+T$ までを指定した時間刻み dt から逐次的に定まる $N=\lfloor T/dt\rfloor$ 個からなる$m$次元ベクトル値のリスト [$\boldsymbol{x}_0$, $\boldsymbol{x}_1$, $\dots$, $\boldsymbol{x}_N$] を返す（3行目で $\boldsymbol{x}_0$ を $\boldsymbol{x}$ とおいて、while文で更新した点を orbit.append(list(x)) によって数値軌道リスト orbit に次々と追加している）。

def euler_orbit(x0, T, dt, vectorfield):
    width = len(x0)
    x = x0
    t = 0
    orbit = []
    orbit.append(list(x))
    while t <= T:
        vx = list(map(lambda v: v(t, *x), vectorfield))
        for i in range(width):
            x[i] += dt * vx[i]
        orbit.append(list(x))
        t += dt
    return(orbit)

8行目でPython的技法 vx = list(map(lambda v: v(t, *x), vectorfield)) を使っている。 *x は可変長引数）を表す。 lambda v: v(t, *x) は無名関数（ラムダ関数）として、t, *x をセットして関数v(t, *x)を定義している。 ただし、この関数vの実体はmapを使って、ベクトル場 $\boldsymbol{v}(t,\boldsymbol{x})$ を定めている関数名のリストvectorfildから得ていることがポイントである。

mapはリストvectorfildから各関数要素（オブジェクト）を取り出して無名関数定義に渡す。 無名関数lambda v: v(t, *x)は既に値が格納された引数tと可変引数*x を使って関数値を計算する。 その結果、vxには与えられた点でのベクトル場値$\boldsymbol{vx}$がリストとして格納されている。

vxはリストであるため、値$\boldsymbol{x} + dt \cdot\boldsymbol{vx}$ を計算して改めて $\boldsymbol{x}$ とするために 9,10行目のように、for文を使ってリスト要素毎の代入計算 x[i] += dt * vx[i] をしている。

可変長引数

Pythonの記号であるアスタリスク (*) は通常、乗算（掛け算）として利用される（文字列についても 'apple' * 4 は 'appleappleappleapple' と掛け算の意味として使う）。 しかし、関数定義の際の引数の並びに、アスタリスク (*) を1つ付けて可変長引数（variable arguments）の意味を持たせるように使うことができる。 アスタリスク (*) を2つ付けてキーワード可変長引数とすることもできる。 関数定義において、引数にアスタリスク (*) を1つ付ける任意の個数の引数が、１つのタプル型オブジェクト（括弧 ( と ) に挟まれたカンマ区切りの並び）の要素に格納される。

次の例を見てみよう。関数 func は形式的には x, y および arg の3つの引数を取るように見えるが、'a', 'b', 'c', 'd', 'e', 'f' の6つの引数を与えると、x に 'a' が、y に 'b' が、そして arg には残りの 'c', 'd', 'e', 'f' がセットされたことがprintで確認できる。 つまり、引数 x, y 以降に渡した任長さの引数並びが args にタプル型オブジェクトの要素として格納されたことが分かる。

>> def func(x, y, *args):
>>     print a, b, args
>> print func('a', 'b', 'c', 'd', 'e', 'f')
('a', 'b', ('c', 'd', 'e', 'f'))
>> print func('a', 'b', 'c', 'd')
('a', 'b', ('c', 'd'))
>> print func('a', 'b', 'c')
('a', 'b', ('c',))
>> print func('a', 'b')
('a', 'b', ())

Euler法でLorenz系を解いてみる

Lorenz方程式（式 (25), (26), (27)）をEuler法で解いてみよう。 次のスクリプト diffeq_lorenz.py は、ベクトル場 vector = [v1, v2, v3] で定まるLorenzの微分方程式を初期点 x0 = [0.1, 0.1, 0.1]、時間区間 T = 20 、刻み幅 0.01 で（Euler法を逐次的に適用して）2000個の要素からなる軌道リスト orbit を求めている。

ここでは、グラフィックス描画モジュール matplotlib とその関連モジュールを使って、解軌道を3次元プロットしている。 描画された画像はマウスで回転して解軌道の様子が観察できる。

# -*- coding: utf-8 -*-
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d.axes3d import Axes3D# for 3dim plot

# vector fields v1, v2, v3 of the right hands of Lorenz eq.
p, r, b = 10.0, 28.0, 8.0/3.0
def v1(t, x, y, z):
return(-p * x + p * y)
def v2(t, x, y, z):
return(-x * z + r * x - y)
def v3(t, x, y, z):
return(x * y - b * z)

def euler_orbit(x0, T, dt, vectorfield):
width = len(x0)
x = x0
t = 0
orbit = []
while t <= T:
    orbit.append(list(x))
    vx = list(map(lambda v: v(t, *x), vectorfield))
    for i in range(width):
        x[i] += dt * vx[i]
    #print x,
    t += dt
return(orbit)

vector = [v1, v2, v3]
x0 = [0.1, 0.1, 0.1]
dt = 0.01
T = 20

orbit = euler_orbit(x0, T, dt, vector)
#print(orbit)

xlist = []
ylist = []
zlist = []
for x, y, z in orbit:
    xlist.append(x)
    ylist.append(y)
    zlist.append(z)

# plot in 3-din space
fig = plt.figure()
ax = fig.gca(projection='3d')
ax.plot(xorbit, yorbit, zorbit)
#ax.plot(orbit[:][0], orbit[:][1], orbit[:][2])# <= !!!! Not CORRECT !!!!
ax.set_xlabel('x(t)')
ax.set_ylabel('y(t)')
ax.set_zlabel('z(t)')
plt.show()

ここでは、グラフィックス描画モジュール matplotlib とその関連モジュールを使って、解軌道を3次元プロットしてみよう。 描画された画像はマウスで回転して解軌道の様子が観察できる。 次のプログラムの先頭の2,3,4行は先のスクリプト diff_euler.py の先頭でインポートする。 先のスクリプトdiff_euler.pyの32行目の後に、以下の11行目以下を加えておく。 モジュールmatplotlibを使って描くために、 時間刻み dt ごとに逐次的に求めた x,y,z-成分リスト[$x_i$,$y_i$,$z_i$](i=$0,1,2,\dots$)からなるリストから、x-成分、y-成分およびz-成分だけが並んだリスト xorbit, yorbit , zorbitを用意している。 22行目でこれらのリストをmatplotlibに渡して軌道を描いている。 このような形でプロットするのはnumpyやmatplotlibの仕様である。

# -*- coding: utf-8 -*-
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d.axes3d import Axes3D# for 3dim plot
....
....
orbit = euler_orbit(x0, T, dt, vector)

xlist = []
ylist = []
zlist = []
for x, y, z in orbit:
    xlist.append(x)
    ylist.append(y)
    zlist.append(z)

# plot in 3-din space
fig = plt.figure()
ax = fig.gca(projection='3d')
ax.plot(xorbit, yorbit, zorbit)
ax.set_xlabel('x(t)')
ax.set_ylabel('y(t)')
ax.set_zlabel('z(t)')
plt.show()

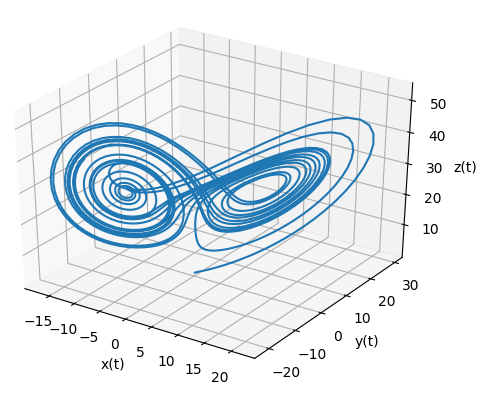
p=10, r=28.0, b = 8.0/3.0のとき、Euler法によるLorenz系の軌道。 初期条件 (0.1,0.1,0.1), 時間刻み dt = 0.01, 時間 T = 10.

Numpyを使って効率化を図る

上のスクリプトの9-15行目のようにして matplotlibに渡すデータを整形することが二度手間のように思える。 Euler法で得られる軌道要素のリストは長さ3の$x,y,z$成分からなるリストを要素としたリスト(長さ$N$とする）で、数学的には$N\times 3$（$N$行3列）の行列である。 目的とするxorbit, yorbit および zorbit は、この$N\times 3$行列の各列の要素からなるリストである。

モジュール NumPy はこうした場合に強力な手段を与える。 NumPy (通常 import numpy as np としてインポートされる）で最も重要なクラスnp.ndarray(object) を使うと多次元配列の簡単で多彩な取扱が可能になる（objectの各次元ごとの要素数が等しいとする）。 クラス np.ndarray のコンストラクタとして通常 np.array(リスト) によって（多次元配列を）生成する。

この事実はSciPyで微分方程式を解くで積極的に使われる。

次のPython Shellの例を見てみよう。 多次元リスト a は$4\times 3$の配列とみなせる。 Pythonでは多次元リスト a のスライス（要素の切り出し）は a[i][j]などと行われるが、このままでは各行または各列の要素全体をスライスできない。 3行目は a[1][2]} で行列の2行目3列目の要素を取り出す。 5行目の結果は、a[:]でリスト全体が取り出され、a[:][2]でのインデックス2の要素を返すが、全行にわたって3列目の要素全体は返さない。

>>> import numpy as np
>>> a = [[1,2,3], [4,5,6], [7,8,9], [10,11,12]]
>>> a[1][2]
6
>>> a[:][2]
[7, 8, 9]
>>> na = np.array(a)
>>> na[:, 2]
array([ 3,  6,  9, 12])
>>> na[1, :]
array([4, 5, 6])

7行目で na = np.array(a) とリストをndarray化すると、8行目で行列の3列目全体、10行目で2行目全体が arrayとして取り出されていることがわかる。 ndarry化したときの行列要素 A のスライスの形は A[j, k] であって、A[j][k] でないことに注意する。

さて、NumPyを使って求めた軌道要素リスト orbit を3行目で nporbit = np.array(orbit) と$N\times 3$行列としてndarray化する。 このとき、各列要素 xorbit, yorbit, zorbit を別途計算することなく、16行目のようにしてmatplotlibで描かせることができる。

....
orbit = euler_orbit(x0, T, dt, vector)
nporbit = np.array(orbit)

#xorbit = []
#yorbit = []
#zorbit = []
#for x, y, z in orbit:
#    xorbit.append(x)
#    yorbit.append(y)
#    zorbit.append(z)

# plot in 3-din space
fig = plt.figure()
ax = fig.gca(projection='3d')
ax.plot(nporbit[:, 0], nporbit[:, 1], nporbit[:, 2])
.....

Runge-Kutta法

演習：調和振子の微分方程式で分かるように、Euler法は誤差が単純に蓄積し、真の解から急速に遠ざかってしまい、実用的には微分方程式の数値解としては精度は十分ではない。 Runge-Kutta法は時間刻み dt の中間点を使って大幅に誤差の発生を抑える工夫がな微分方程式の数値計算法である。

次で定義したPython関数 runge_kutta_orbit(x0, T, dt, vectorfield) は、Runge-Kutta法を使って解軌道の数値リストを求めている。 vectorfield はベクトル場 $\boldsymbol{v}$ を定める $m$ 個の関数リスト [$v_1$, $\dots$, $v_m$] である。 時刻 $t_0$ における$m$次元（2行目の width に次元の値が格納される）の初期点リスト x0 =[$x_{01}$,$\dots$,$x_{0m}$]から出発して、時刻 $t_0$ から $t_0+T$ までを指定した時間刻み dt から逐次的に定まる $N=\lfloor T/dt\rfloor$ 個からなる$m$次元ベクトル値のリスト [$\boldsymbol{x}_0$, $\boldsymbol{x}_1$, $\dots$, $\boldsymbol{x}_N$] を返す。 3行目でリストx0 を xに代入して、while文で更新した点を orbit.append(list(x)) によって数値軌道リスト orbit に次々と追加している。

Euler法とは異なり、while文内で時刻 $t_n=n\Delta t$ に求めた値 $\boldsymbol{x}_n$ から次の時刻 $t_{n+1}=t_n + dt$ での値 $\boldsymbol{x}_{n+1}$ を求めるために、22,23行目で中間の刻み幅 dt/2 を使った増分を計算した k1, k2, k3, k4 を使っている（計算量は4倍になる）。

def runge_kutta_orbit(x0, T, dt, vectorfield):
    width = len(x0)
    x = x0
    t = 0.0
    orbit = []
    while t <= T:
        orbit.append(list(x))
        x1 = x
        # python3 requests list() as below:
        k1 = list(map(lambda v: v(t, *x1), vectorfield))
        x2 = x
        for i in range(width):
            x2[i] += dt / 2.0 * k1[i]
        k2 = list(map(lambda v: v(t + dt / 2.0, *x2), vectorfield))
        x3 = x
        for i in range(width):
            x3[i] += dt / 2 * k2[i]
        k3 = list(map(lambda v: v(t + dt / 2.0, *x3), vectorfield))
        x4 = x
        for i in range(width):
            x4[i] += dt * k3[i]
        k4 = list(map(lambda v: v(t + dt, *x4), vectorfield))
        for i in range(width):
            x[i] += dt / 6.0 * (k1[i] + 2.0 * k2[i] + 2.0 * k3[i] + k4[i])
        t += dt
    return(orbit)

数値解の誤差

時間刻み $\Delta t$ を小さくすることが望ましいことは明かである。 正しい結果は $\Delta t\rightarrow 0$ の極限で「のみ」もたらされるのであって、微分方程式の数値解から得られ結果は真の解ではない。 しかし、$\Delta t$ を小さくすればするほど、同じ計算法でも時間経過は遅くなり計算量が増す（それでも有限の時間刻みで計算している以上、誤差の存在から逃れられない）。

また、時間刻み $\Delta t$ を一定にする積極的な理由もない。 ベクトル場 $\boldsymbol{f}(\boldsymbol{x},t)$ が急峻なときには、わずかな $\Delta t$ であっても大きな変化 $\boldsymbol{x}(t+\Delta t)-\boldsymbol{x}(t)$ をもたらすため、そのような箇所では時間刻みを細かくすることが望ましい。 たとえば、万有引力やCoulomb力のように距離の二乗に反比例する力が働くとき場合である。 仮に、衝突解がもたらされる場合、その原因が数値誤差に起因するか、実際に起こり得る現象化を吟味することは容易いことではない。

常微分方程式の数値解法は、ここで取り上げた中間点を考慮して精度を向上させるRunge-Kutta法など実用上広く用いられている方法がいくつかあるが、誤差限界は存在している。 非線形方程式では、たとえばLorenz方程式のような単純な場合でも真の解の挙動が知られていないために、それ自体が研究対象になり得る（Smale(1998)の Mathematical Problems for the Next Century（Mathematical Intelligencer 20 (2): 7–15）の問題14）。 実際、 精度保証付き数値計算の研究は W. Tucker(2002)の A Rigorous ODE Solver and Smale’s 14th Problemによって非線形常微分方程式については一応の解決をみたが（参考：「 \href{http://www.math.sci.hokudai.ac.jp/~zin/papers/kokyuroku.pdf}{精度保証付き数値計算の力学系への応用について}）、偏微分方程式においては依然として大きな研究テーマであり続けている。 明日に天気予報についても断定できるほどの確度はまだない。

---

Copyright 2004 水谷正大