Webページでは数式を表すためにLaTeX表記が使えるMathJaxを利用しています。 WebブラウザにはSafari/Chrome/Firefoxを使って下さい（IEでは表示できないようです。）

Webの数式表現

Webの数式表現はきわめて大切で、Web技術を使う電子書籍（たとえばEPUB形式の電子書籍）における数式表示の需要がある。

LaTeXで生成したPDFファイルから数式を切り出した画像としてWebページ貼り込めは済むわけではない。 Webの表示はPDFのようなページレイアウト固定でなく、ウィンドウサイズやフォントの大きさによってレイアウトが変化するreflow型）であるので、画像の貼り込みでは読みやすい数式表示とはならない。 また、画像の貼り込みではページコンテンツから数式内容を読み取る処置ができない。

Webページでの数式表現には幾つかの提案がある。

blue-sqMathMLの利用
数式を記述するMathML（Mathematical Markup Language）を定義し、これを理解するWebブラウザで表示する。
blue-sqMediaWikiによるTeX組版の利用
MediaWikiソフトウェアがLaTeX互換の表式をソフトウエアTexvcによってMathML出力を生成して、Webページにレンダリングを行う。 GNU General Public Licenseで配布されている。。 Wikisourceの高木貞治プロジェクトで利用されている。
blue-sqMathJaxの利用（ここで取り上げる方法）
JavaScriptによって各種LaTeX表式をWebページにレンダリングするオープンソースソフトウエア。 アメリカ数学会(AMS)と工業応用数学会(SIAM)とのMathJaxコンソーシアムで開発されている。 複雑な数式のWeb表現のために、筆者の知る範囲ではもっとも簡便である。

MathJaxの利用

このページもそうであるが、MathJaxを利用してWebページ内にLaTeX表式を使って数式表現を行うことは簡単である。 HTMLファイルのヘッダ部（<head>と</head>の間）に次のように記述する。 

<head>
....
<script type="text/javascript"
  src="http://cdn.mathjax.org/mathjax/latest/MathJax.js?config=TeX-AMS-MML_HTMLorMML">
</script>
<script type="text/x-mathjax-config">
  MathJax.Hub.Config({
    TeX: { equationNumbers: { autoNumber: "AMS" }},
    tex2jax: {
      inlineMath: [ ['$','$'], ["\\(","\\)"] ],
      processEscapes: true
    },
    "HTML-CSS": { matchFontHeight: false },
    displayAlign: "left",
    displayIndent: "2em"
  });
</script>
....
</head>

MathJaxを使うことを3-5行目で宣言しており、Webブラウザ側の処理に必要なJavaScriptである MathJax.js をWebサイト cdn.mathjax.org から読み込むように指定している。 ここでは、TeX-AMS-MML_HTMLorMML を指定することによって、TeX、LaTeXの標準的記法だけでなく、AMSmath と AMSsymbols パッケージを使ったAMS-LaTeX表式も表現可能としている。

したがって、上記のようにして MathJaxを利用して数式をつかったコンテンツを作成・確認するためにネットワーク環境下での作業が必要である（MathJaxで利用するJavascriptをローカルに置くことも可能である）。

6-17行目はMathJax表示を調整している。 7行目は、HTML本文でLaTeXと同じように $\backslash [$ と $\backslash ]$ で挟まれた箇所に数式番号無しで数式を書くためのMathJaxスクリプトである（ここでは \$\$ と \$\$ の代わりに $\backslash [$ と $\backslash ]$ を使うとしている）。 11-12行目は、数式を中央揃えでなく左から全角2文字分くらいで揃えるよう指定している（11,12行を書かないと、数式は中央揃えとなる）。 これらの詳しい意味はLoading and Configuring MathJaxに説明があるので必要に応じて参照して欲しい。

Math MLとの比較

Webページに数式を表示するためにW3C が標準化を進めている書式 MathML がある。 よく考えられているのだがMathML 耐久テスト参照）、一番の問題はMathMLとして数式を表すための記述コード量が多くなること、そしてMathJaxがそうであるようにLaTeX記述でWebページに数式を表示できる

MathJaxを使ってLaTeXのようにして $4 \sin^2(x)-4 \cos^2(x)$ を表示するごく単純な表現 $\$4 \backslash sin \^2(x)-4 \backslash cos \^2(x)\$$ はMathMLでは次のように長大になる。 LaTeX表式が数式を美しく簡素に表現できることがわかる。 4 sin 2 x - 4 cos 2 x 

<math>
    <mn>4</mn>
    <msup>
      <mi>sin</mi>
      <mn>2</mn>
    </msup>
    <mi>x</mi>
    <mo>-</mo>
    <mn>4</mn>
    <msup>
      <mi>cos</mi>
      <mn>2</mn>
    </msup>
    <mi>x</mi>
</math>
演習： 上のMathMLをHTMLファイルに書いて、ブラウザで閲覧しなさい。

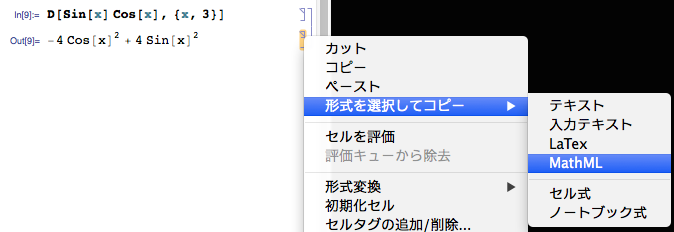
mathematica_mathm

上のMathMLのコードはMathematicaの出力をMathMLで書き出してHTMLにペーストした。 右図（クリックで拡大）のように、MathematicaではLaTeX形式で書き出すことも可能だ。


MathJaxの数式表示

このページでも使っているMathJaxによる数式表現のためはLaTeXの数式をHTML本文に書けばよい。 実例付きコマンド一覧には TeX Commands available in MathJaxを参照（表示には時間がかかる）。

演習： 以下の数式表現をHTMLファイルに記述して、Webページとして表示しなさい。 LaTeX表記とその表示との対応をよく理解することが大切だ。

光は真空中を1秒間に約 $3.0 × 10^8$ メートル進む。 光速を $c$ で表す。 

光は真空中を1秒間に約 $3.0 × 10^8$ メートル進む。
光速を $c$ で表す。

$x^2=2$ を満たす数 $x$ は、2の平方根 $\sqrt{2}$ を使って $x=\pm\sqrt{2}$ と表される。 数 $\sqrt{2}$ は \[ \sqrt{2} \approx 1.41421356237 \] である。 

$x^2=2$ を満たす数 $x$ は、2の平方根 $\sqrt{2}$ を使って $x=\pm\sqrt{2} と表わされる。
数 $\sqrt{2}$ は
\[
\sqrt{2} \approx 1.41421356237
\]
である。

\[ \sum_{k=1}^n k = 1+ 2+ \dots + n=\frac{n(n-1)}{2} \] 

\[
\sum_{k=1}^n k = 1 + 2 + \dots + n = \frac{n(n-1)}{2}
\]

2次方程式 $ax^2 + bx + c =0$ の根の公式は \[ x=\frac{-b\pm\sqrt{b^2-4ac}}{2a} \] である。 

2次方程式 $ax^2 + bx + c =0$ の根の公式は
\[
x=\frac{-b\pm\sqrt{b^2-4ac}}{2a}
\]
である。

$(a+b)^n$ は2項係数 $\displaystyle\binom{n}{n-k}=\frac{n!}{(n-k)!\times k!}$ を使って \[ (a+b)^n=\sum_{k=0}^n \binom{n}{n-k}a^{n-k}b^k \] 

$(a+b)^n$ は2項係数 $\displaystyle\binom{n}{n-k}=\frac{n!}{(n-k)!\times k!}$ を使って
\[
(a+b)^n=\sum_{k=0}^n \binom{n}{n-k}a^{n-k}b^k
\]
と表される。

Fibonacci数列 $\{f_n\}$ は次のように定義される。 \begin{align*} f_0 &= 1\\ f_1 &= 1\\ f_n &= f_{n-1}+f_{n-2}, \qquad n\geq 2 \end{align*} 

Fibonacci数列 $\{f_n\}_{n=0}$ は次のように定義される。
\begin{align*}
f_0 &= 1\\
f_1 &= 1\\
f_n &= f_{n-1}+f_{n-2}, \qquad n\geq 2
\end{align*}

\begin{align} \langle f_1(x)\,|\, \phi(x-\ell)\rangle_{L^2} &= \sum_k c^*_k\int_{-\infty}^\infty \phi\left(2(t-\frac{k}{2})\right)^*\phi(t-\ell)\,dt\\ &= \sum_\ell \left\{ c_{2\ell}\int_{\ell}^{\ell+\frac12}\phi\left(2(t-\ell)\right)^*\phi(t-\ell)\,dt \right. \nonumber \\ & \left. \qquad + c_{2\ell+1}\int_{\ell+\frac12}^{\ell+1}\phi\left(2(t-\ell-\frac12)\right)^*\phi(t-\ell)\,dt\right\} \\ &=0 \quad\text{であるためには $c_{2\ell}=-c_{2\ell+1}$ に限る} \nonumber \end{align} 

\begin{align}
\langle f_1(x)\,|\, \phi(x-\ell)\rangle_{L^2} 
&= \sum_k c^*_k\int_{-\infty}^\infty 
     \phi\left(2(t-\frac{k}{2})\right)^*\phi(t-\ell)\,dt\\
&= \sum_\ell \left\{ c_{2\ell}\int_{\ell}^{\ell+\frac12}
     \phi\left(2(t-\ell)\right)^*\phi(t-\ell)\,dt \right. \nonumber \\
& \left. \qquad + c_{2\ell+1}\int_{\ell+\frac12}^{\ell+1}
     \phi\left(2(t-\ell-\frac12)\right)^*\phi(t-\ell)\,dt\right\} \\
& = 0 \quad\text{であるためには $c_{2\ell}=-c_{2\ell+1}$ に限る} \nonumber
\end{align}

MathJaxでWebページを書こう

演習： 次の数式をWebページに表示しなさい。 \[ \frac{\pi}{2} = \sum_{k=0}^{\infty} \frac{(2k)!}{2^{2k}(k!)^2} \frac{1}{2k+1} = \prod_{k=1}^{\infty} \frac{4k^2}{4k^2 - 1} \]