
この授業では、Anaconda というデータサイエンスや機械学習を含む科学技術計算向けの Python のプラットフォームです。
プログラミング演習 I では、Jupyter Notebook を用いて Python のプログラミングを行なったかもしれませんが、
Anaconda をインストールすることで、
Jupyter Notebook やその上位互換的な位置付けの Jupyter Lab などを簡便に使うことができる様になります。
Google Colaboratory という Google が提供するクラウド環境上で Jupyter Notebook を
利用することもできますが、この授業では Anaconda をインストールしてローカル(自分のPC上)でプログラムを動かします。
Google Colaboratory 上で動いていたプログラムがそのまま動かせるわけではないことに注意してください。
まずは、こちらの Anaconda の公式サイトから インストーラーをダウンロードして、自分の Mac にインストールしてください。
サイトに接続したら、緑色の "Download" をクリックするか、ページの下まで移動してください。
どちらの場合でも、自分の使っている Mac に応じてダウンロードするファイルを選択してください。
基本的には、2021年度以前入学の学生は Intel と書かれている方をダウンロードすれば問題ないはずです。
2022年度以降入学の学生は、基本的には Apple Silicon と書かれた方をダウンロードしてください。
ダウンロードが完了したら、インストーラーを開いて指示に従ってインストールしてください。 インストール先については特に変更する必要はないでしょう。
インストールが完了したら、アプリケーションとして Anaconda-Navigator が利用可能になりますので、 起動してみましょう。

起動すると、画面のようにアップデートの確認が出る場合があります。
これが出た場合には、利用を始める前にアップデートしてしまいましょう。
具体的には、アップデートの確認に対して "Yes" を選択します。
ただし、Anaconda-Navigator を開いたままではアップデートできないので、一旦閉じてからアップデートを行います。
アップデートが完了したら、再び起動してみると以下の様な画面が出てきます。
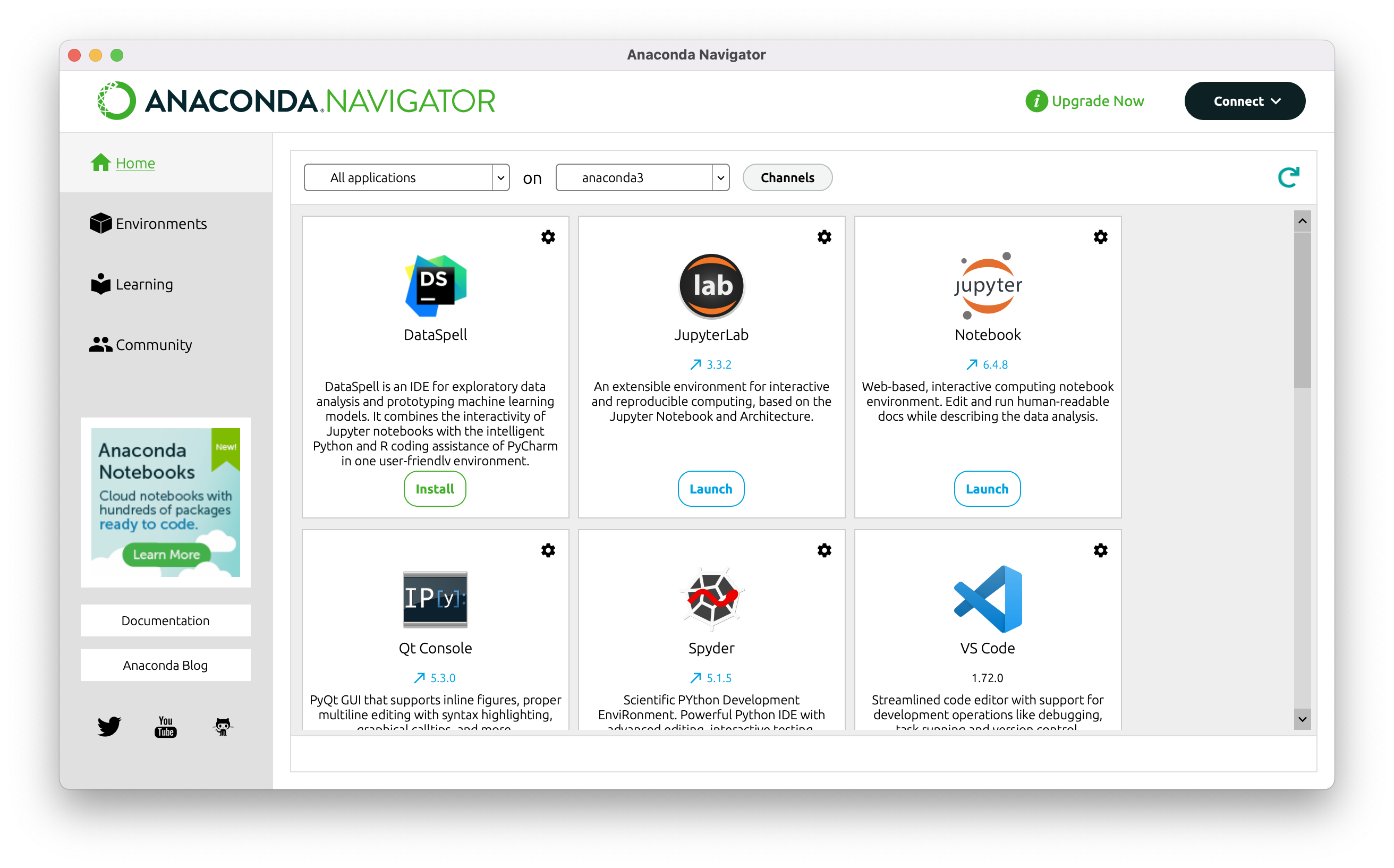
この画面から、Jupyter Notebook や JupyterLab、Spyder といったアプリケーションを起動することができます。
今後この授業では、JupyterLab と場合によっては VS Code を利用していきます。
Jupyter Notebook を利用するのでも基本的には問題ありませんが、
授業資料の画像では JupyterLab を利用していますので、その点だけ注意して下さい。
それぞれのアプリケーションは、"launch" で起動することができます。
アプリケーションによっては "Install" と表示されているものもあるので、インストールしてから利用することになります。
とりあえず今日は、JupyterLab を利用してみることにしましょう。
起動すると、Jupyter Notebook の時と同様にブラウザ上で JupyterLab が起動して、以下の様な画面が出てきます。
ここでは、一番上の Notebook の Python3 を選択します。

すると以下のような画面が出てきますので、こちらでプログラムをしていきます。
セルの中にコードを書き、左側の横向き三角マークを押す(あるいは、command + Enter を押す)とプログラムが実行されます。
次に、以下の1次元ランダムウォークのプログラムが動くかを確認してみましょう。
(1次元ランダムウォークについては、プログラミング演習 I でやっているはず?2次元はこの演習でやります)
以下のソースコードを貼り付けて、実行してみましょう。(ここでは、中身については説明しません)
上の方にある「+」を押せば(あるいはキーボードで「B」を押せば)新しいセルを追加できるので、
追加したセルに貼り付けて実行してみましょう。
import numpy as np
import numpy.random as rd
import matplotlib.pyplot as plt
N = 100
r = rd.randint(0,3,N)
s = np.zeros(N)
s[0] = 0
for i in range(N-1):
if r[i] == 0:
s[i+1] = s[i] + 1
elif r[i] == 1:
s[i+1] = s[i] - 1
else:
s[i+1] = s[i]
x = np.arange(N)
plt.plot(x,s)
plt.show()
以下のようなグラフが描画されれば、成功です。(グラフの形状は実行ごとに変わるので、グラフが表示されればOKです)
今日の授業ではここまで確認できれば問題ありません。
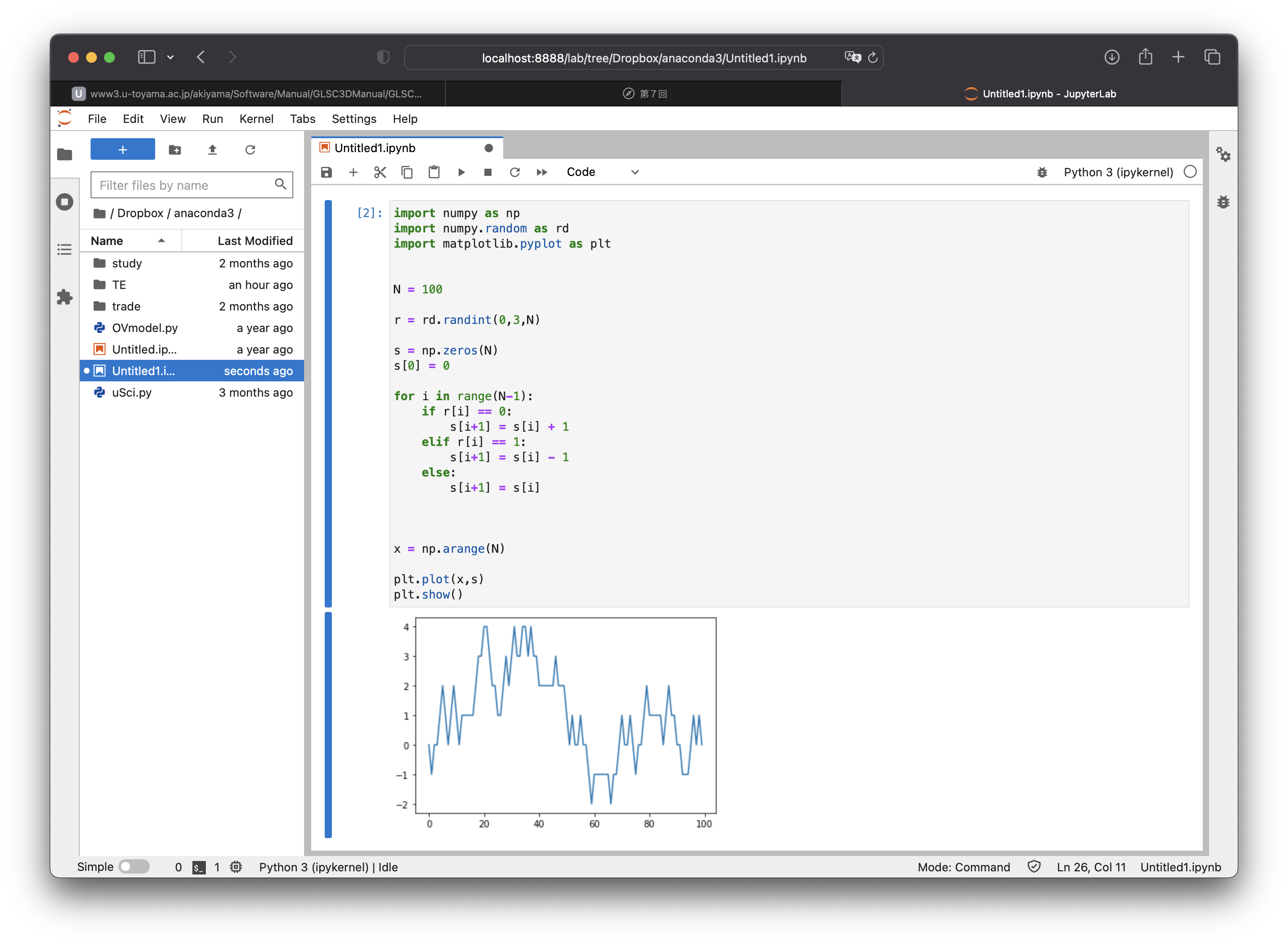
上で表示させた1次元ランダムウォークの実行画面のスクリーンショットを撮って、その画像ファイルを提出してください。
スクリーンショットの撮り方は、以下に示した通りです。
その他、表示されているグラフの画像をそのままFinderへドラッグ&ドロップすることで保存することも可能です。
(これは言葉では分かりづらいので、授業内で実演します)
詳しくは、こちらを参照してください。
画面全体のスクリーンショットで必要ない部分を切り取るのが面倒な場合には、 ウィンドウのスクリーンショットを撮る(「command + shift + 4」の後、スペースを押し、撮りたいウィンドウをクリック) のが便利です。
「課題」で作成した画像ファイルを提出してください。
画像ファイルの名前は特に指定しません。
また、提出したファイルが正しいものであるかどうかは、毎回確認するよう習慣づけてください。
提出締め切り: 2024年11月18日19時
今回の授業の残り時間は、中間レポート課題に取り組む&中間レポート課題に対する質問を 受け付ける時間になります。 締切前の最後の授業になるので、分からないことは今日の授業内で聞いておくようにしてください。
また、すでに提出されている中間レポート課題の中には、文頭や文中の説明が不十分なものが少なからず見受けられます。 自分の言葉で十分に説明するようにしてください。 他にも、プログラムが見やすいように適切に字下げを行っていないものも見受けられますので、採点基準を今一度見直して適宜修正を行ってください。
コッホ曲線とは、以下の操作を繰り返すことにより得られる図形である。
1. 直線を引く
2. 直線を3等分する
3. 直線を等分した2点を頂点とする正三角形をつくる
4. 出来上がった各線分について2、3を繰り返す
上記の操作を適当な回数(十回程度)繰り返して得られる図形を描くGLSC3Dのプログラムを作成せよ。 以下に、そのようなプログラムの実行例をあげる。
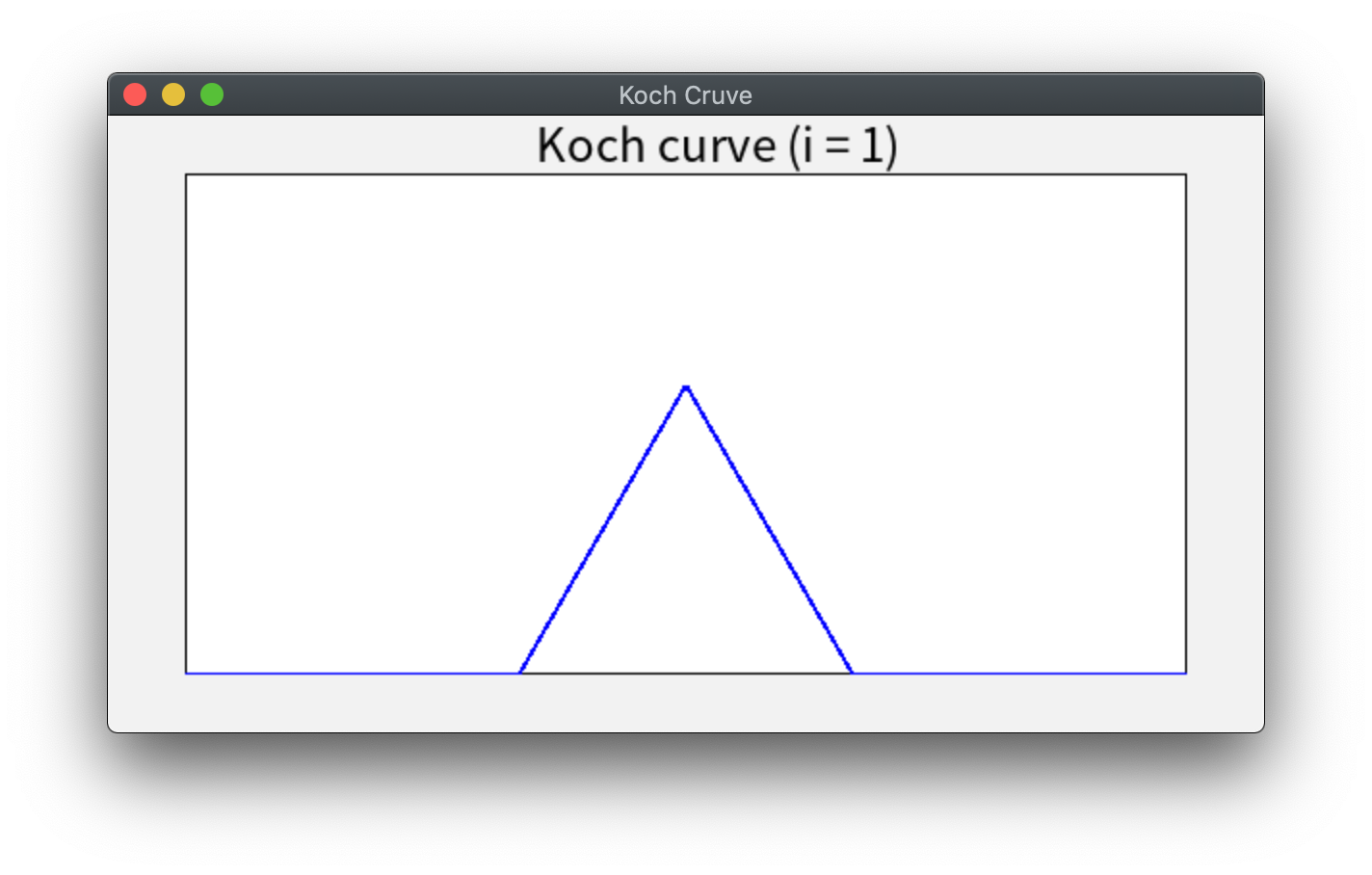
青い直線を3等分し、等分した2点で正三角形を作ったところ。4つの線分にわかれた。
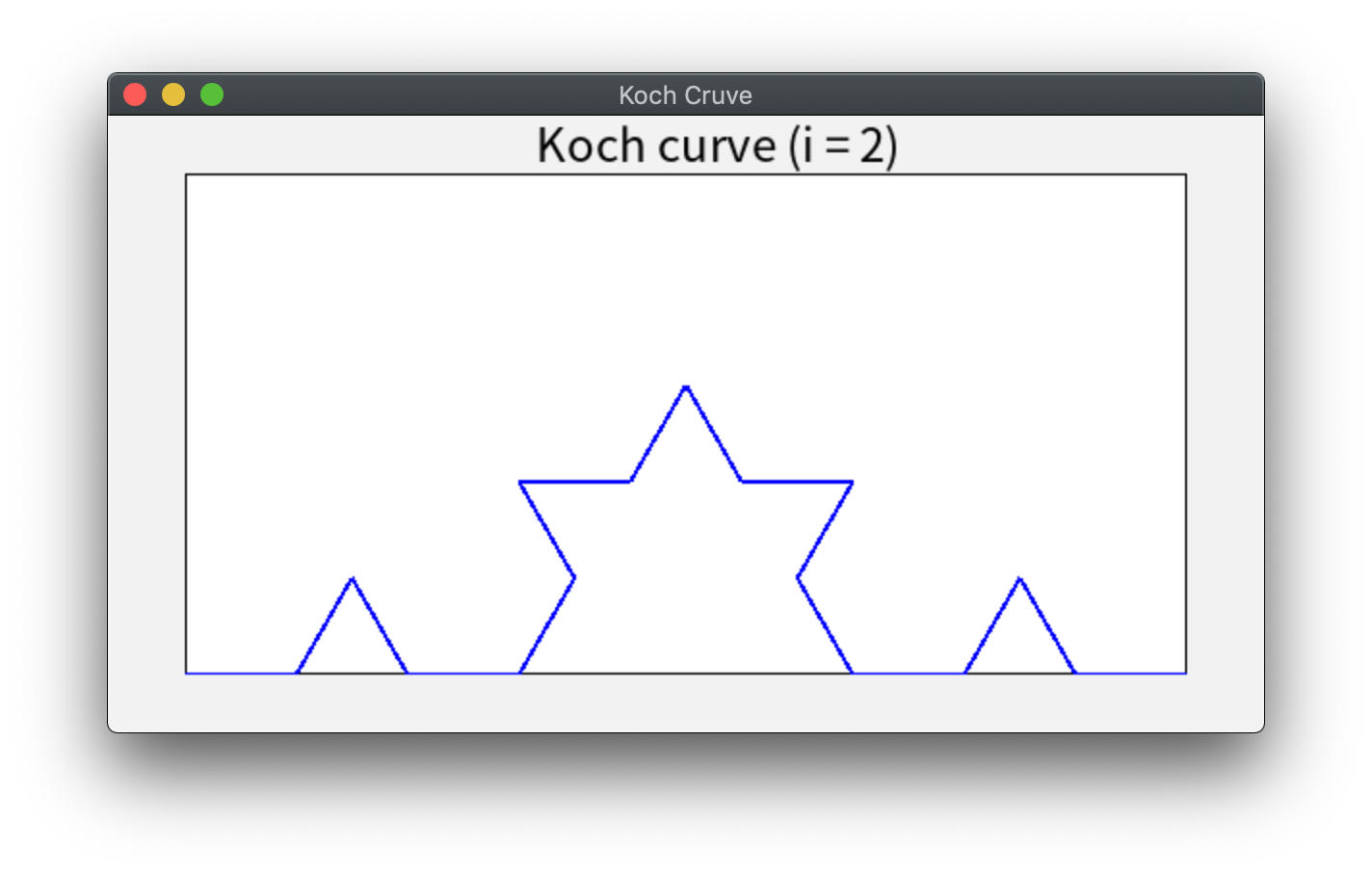
上で得られた4つの線分に対して、同様の操作(それぞれの線分を3等分し、等分した2点で正三角形を作る)を経て得られた図形。 16の線分により構成される図形となる。 次も同様に、その16の線分全てについて同様の操作を行う。 以下、これを繰り返していく。
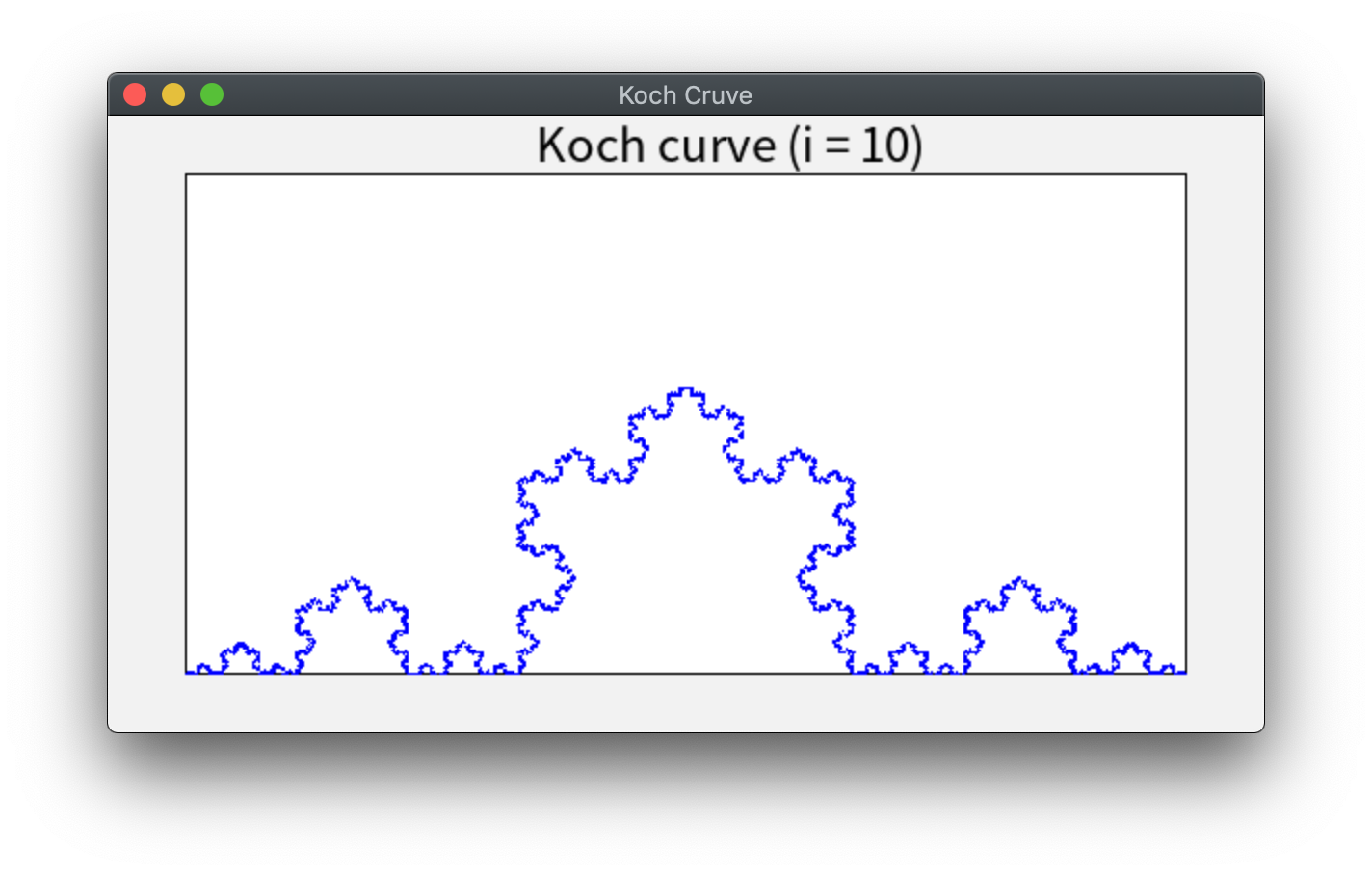
上記手続きを10回繰り返した後得られた図形。実際には、細かすぎるため5回目くらいから見た目はほとんど変化していない。 10回繰り返した場合、線分は 4^10 = 1,048,576 本になるので、 さらに繰り返しが増えると描画にかなりの時間を要する。
関数の再帰呼び出しを使えば簡単だが、関数の再帰呼び出しを使わなくてもできるので、関数の再帰呼び出しの知識が無くてもよい。
上記の関数 Koch をmain 関数内で一度呼び出すことにより、指定した繰り返しの回数分の処理を行った Koch 曲線が描画される。
点 C, D, E の計算方法については、以下を参照。
