第５回 C言語による現象のシミュレーション１ (2024年10月21日)

今日の内容

rand() 関数

rand() 関数は、その関数が呼ばれるたびに疑似乱数値として整数値を返します。 例えば、次のプログラムでは１０個の疑似乱数値を画面に表示します。 次のプログラムをエディタに打ち込み（コピペし）、 cc コマンドでコンパイルし、実行してみてください。 （ここでは GLSC3D の関数を使っていないので、通常のＣ言語のプログラムのコンパイル方法と同じく cc コマンドでコンパイルします。 ただし、ccg コマンドでコンパイルしても別段問題は無い。） なんともでたらめな数値が表示されることでしょう。

例１

#include <stdio.h>
#include <stdlib.h>

int main()
{
    int i, r;

    for(i = 0; i < 10; i++)
    {
        r = rand();
        printf("%d\n", r);
    }

   return 0;
}

注意： rand() 関数を使う場合、#include <stdlib.h> が必要となります。
（復習：数学関数を用いるときには #include <math.h> 、GLSC3Dを用いる場合には #include <glsc3d_3.h> がそれぞれ必要であった。）

srand() 関数

rand() 関数は、ある初期値、ある規則に従って求まる数列ですが、何もしないといつも初期値が同じであるため、同じ数列が得られます。 そこで、srand() 関数を用いることで、数列の初期値（正確には、疑似乱数列をつくりだす漸化式の初期値）を変更できます。 利用方法は、

srand(100);

等と、プログラムのはじめの方で一度呼び出すだけです。 今は 100 としましたが、例えば、皆さんの学籍番号等とすれば各自異なる結果が得られます。 ただし、srand() 関数の引数は整数値です。

srand() 関数は例えば以下のように使います。上記サンプルプログラムに srand() 関数を埋め込みました。

例２

#include <stdio.h>
#include <stdlib.h>

int main()
{
    int i, r;

   srand(100);

    for(i = 0; i < 10; i++)
    {
        r = rand();
        printf("%d\n", r);
    }

   return 0;
}

この様に、main() 関数のはじめの方で一度だけ呼び出します。 関数を用いた場合、以下のような例が正しい使い方です。

例３

#include <stdio.h>
#include <stdlib.h>

void foo();

int main()
{
   srand(100);
   printf("1回目\n");
   foo();
   printf("2回目\n");
   foo();

   return 0;
}

void foo()
{
    int i, r;

    for(i = 0; i < 10; i++)
    {
        r = rand();
        printf("%d\n", r);
    }
}

例えば、以下の２つの例は間違いです。 実行すると同じ数値が10個表示されます。（漸化式の初期値をいつも100とし直しているので、当然ですが。）

例４

#include <stdio.h>
#include <stdlib.h>

int main()
{
    int i, r;

    for(i = 0; i < 10; i++)
    {
        srand(100);
        r = rand();
        printf("%d\n", r);
    }

   return 0;
}

以下は関数を使った間違った例。

例５

#include <stdio.h>
#include <stdlib.h>

void foo();

int main()
{

   printf("1回目\n");
   foo();
   printf("2回目\n");
   foo();

   return 0;
}

void foo()
{
    int i, r;

    srand(100);

    for(i = 0; i < 10; i++)
    {
        r = rand();
        printf("%d\n", r);
    }
}

サンプルプログラム

乱数を多く使う場合や [0,1) の一様乱数を用いたい場合には、 次の様に #define 文を利用すると便利です。 #define 文は関数の外側に書き、定数の定義などに使います。 具体的には、

#define COUNT_MAX 10

のように書きます。この場合、プログラム内の COUNT_MAX という表記は、コンパイル時に 10 という値に置き換えられます。 下のサンプルプログラムのように、値だけでなく関数や数式を置き換えることも可能です。

使用する際に注意する点は、#define 文はあくまで置き換えなので、 定義の際に int や double といった「型」を定義しません。 プログラム内で、1.0 や 10 という数値は型を定義せずにそのまま使うのと同じことです。

#define 文を使うのは、プログラムを見やすくするという理由の他にも、 プログラムで何度も出てくる定数の値（例えば、領域の大きさ）を一括して書き換える際にも便利です。 何度も出てくる定数を数値そのままで書いていると、バグの温床になりがちでデバックの際にも苦労するので、 今後はなるべく #define 文を利用するようにしましょう。

例６

#include <stdio.h>
#include <stdlib.h>

#define  COUNT_MAX   (10)
#define  RN   (rand()/(double)RAND_MAX)

int main()
{
    int i;

   srand(100);

    for(i = 0; i < COUNT_MAX; i++)
    {
        printf("%lf\n", RN);
    }

   return 0;
}

時刻を用いた乱数ので初期化

例えば、ゲームなどで乱数を利用する場合、毎回同じではつまらないという場合もあるでしょう。 シミュレーションでは毎回同じ乱数列が得られる（再現性がある）事も大事で、ここで紹介する時刻で初期化する方法はおすすめしませんが、やり方だけは学んでおきましょう。

#include <stdio.h>
#include <stdlib.h>
#include <time.h>
int main() {
	srand((unsigned)time(NULL));
   
	printf("%d\n", rand());
	printf("%d\n", rand());
	return 0;
}

上記をコンパイルして実行すると、実行する度に違う数値がでるでしょう（再コンパイルの必要はありません。）。

time 関数は、グリニッジ標準時(GMT)の1970年1月1日の00:00:00 から現在までの経過時間を秒単位で返します。 （秒単位なので、一秒以内に実行した場合には同じ結果である可能性はあります。） 利用には、 #include <time.h> が必要です。

「擬似」乱数列とは？

今後の授業で行う粒子のランダムウォークのようなシミュレーションする場合、確率的な現象を表すために必要な「サイコロを振る」部分をどのようにするかという問題が発生します。 Ｃ言語には標準関数として疑似乱数生成関数 rand() が用意されています。 （過去においては、rand() 関数が生成する疑似乱数列はあまりよいものではありませんでした。当面この関数を用いて疑似乱数列を得ることにします。）

rand() 関数の問題点については、例えば このサイトの説明などが参考になります。 将来、研究などで擬似乱数を利用する際には、先のサイトでも紹介されているメルセンヌ・ツイスタ等を使うと良いでしょう。
（Python では標準の乱数生成でもメルセンヌ・ツイスタを利用している）

おまけ
ゲームで現れる「ランダム」な要素も全て擬似乱数によって生成されている（はず）。 古いゲーム（スーパーファミコンの時代くらい）では、リアルタイムに乱数を生成するのではなく、乱数テーブル （あらかじめ乱数列を計算してゲームプログラム内部に保持）が用意されていた。 一定の操作を行うことで、好きな乱数を引き出せる「乱数調整」も乱数テーブルがあってのもの。
その他、数学的に正しい乱数列と人間が正しいと感じる乱数列の違いも、大変興味深い。
プレイヤーが自然に感じる乱数の作り方
ドラクエ９攻略：ホイミテーブル技解説
ナムコ作品で見る乱数の歴史
“なんでもあり”な『ドラクエ3』RTAがヤバい。

おまけ

先に、Ｃ言語の標準関数である rand() は、疑似乱数生成関数としてあまり良くないと書いた。 計算機では、有限の情報しか扱えないため、疑似乱数と見なしている数列は周期的であるが、 標準関数の rand() 関数が作り出す疑似乱数列の周期があまり長くない事が理由の一つである。 srand() 関数を用いて、いくつかの乱数列を発生させ、その周期を調べてみよう。 最も短い周期、最も長い周期、周期の平均値などはどのようになるか？ （漸化式を用いて数列を生成するので、同じ数値が現れたらその後は同じ数列が生じる。 つまり、はじめの数値を記録しておいて、同じ数値が再び現れるまでの回数を数えればよい。）

実は最近の rand() 関数は昔のものに比べると良くなっているらしい。

◎課題(難しい)

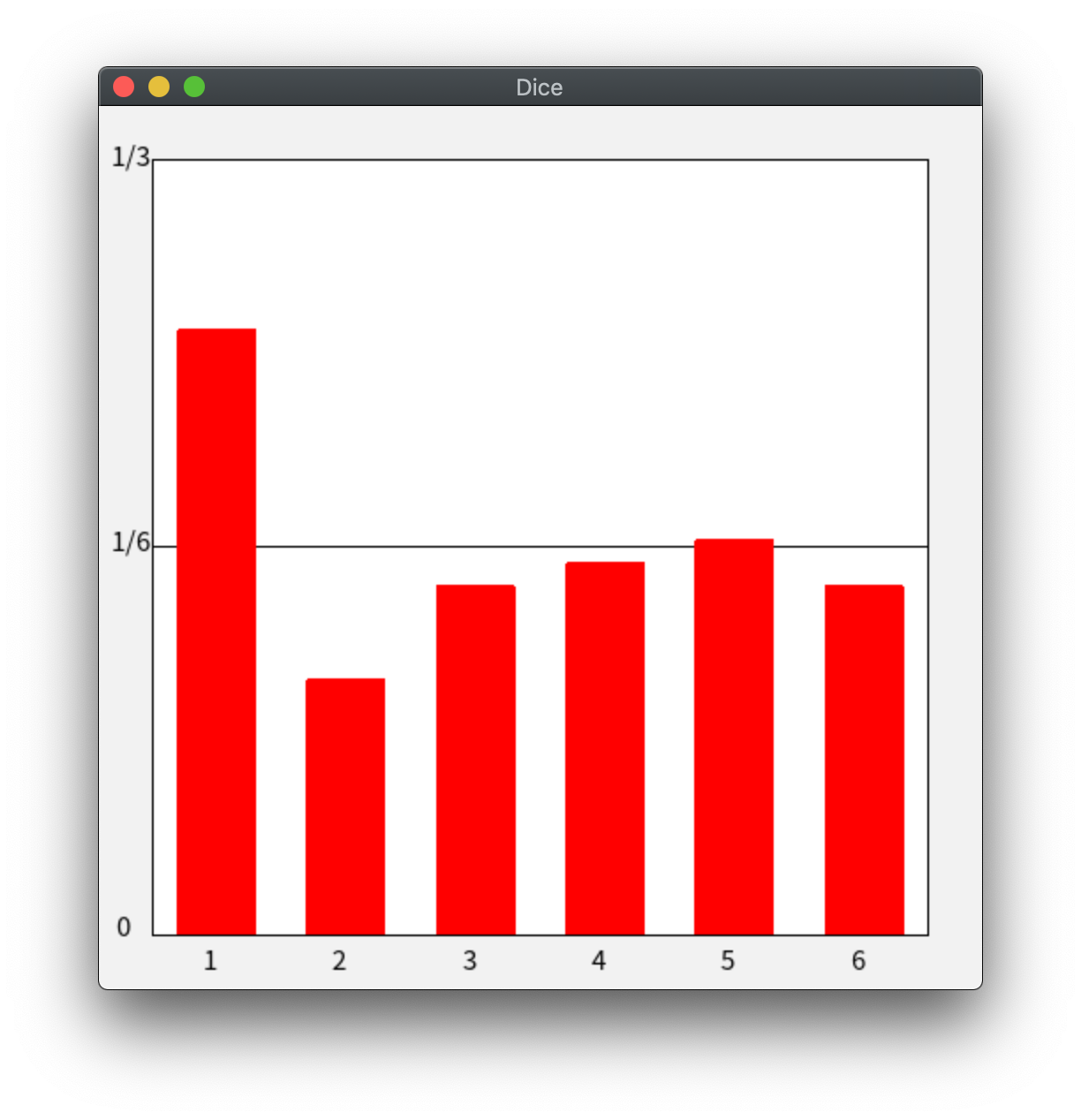
呼ばれる度にランダムに 1〜6 の数値を返す関数 dice() を作成せよ。 その上で、dice() 関数を用いて自分で入力した回数だけサイコロを振るシミュレーションを行い、 1〜6の目が出た回数と確率をターミナル上に表示するプログラムを作成せよ。
また、各目の出た確率については、GLSC3D を用いて棒グラフでも描画せよ （図のように、確率 1/6 の位置に線を引いておくと、出た目の偏りがわかりやすい）。
さらに、1秒ごとに新たなシミュレーション結果（最初に200回と入力したら200回振った結果）を100回表示するように、 プログラムを改良せよ。

ヒント：

・dice() 関数は、1~6 の整数値を返すので、int 型の関数として定義する。
・r = rand() で擬似乱数値を生成したあと r % 6 とすれば、整数 r を 6 で割った剰余（つまり 0〜5）が得られるので、 これを利用して 1~6 のランダムな整数値を取得する。


・サイコロを10000回振ったときに1〜6の目それぞれが出た回数を数えるには、 各目の出た回数を記録する整数型の配列を用意すると良い。
　例えば、

　int  count[6];

　と整数型の配列を用意し、初めに配列の中身を全て 0 に初期化したのち、出たサイコロの目を r として、

　count[r-1]++;

　とすれば良いだろう。r-1 となっているのは、Ｃ言語の配列の添え字が０からはじまることによる。
　もし、０〜５までの乱数を生成した場合には、配列の添え字を r-1 とするのではなく、出た目を r+1 と表示すれば良い。


・入力した回数振った結果を1秒ごとに100回表示するには、以下のようなアルゴリズムになる。

  1. srand 関数で乱数の初期化
  2. scanf 関数でサイコロを振る回数 N を取得
  3. GLSC3D の初期化(g_init) & 自由座標の定義(g_def_scale_2D)
  4. 以下を100回繰り返す（サイコロを N 回振るシミュレーションの結果表示のループ）
    1. サイコロの目の出た回数（配列 count[6]）を初期化
    2. 以下を N 回繰り返す（サイコロを N 回振る）
    3. 出た目の確率を計算（確率の値は double 型なのに対し、count[6] は int 型であることに注意）
    4. 目のでた回数と確率をターミナル上に表示
    5. GLSC3D 関数を用いて、以前の描画の消去 & 今回の結果のグラフ描画
      描画の消去は、g_cls 関数
      グラフの描画は、g_box_2D 関数や g_move_2D & g_plot_2D 関数
    6. g_finish 関数で window に描画
    7. g_sleep 関数で１秒間停止
  5. g_sleep 関数でしばらく停止した後 GLSC3D 終了


・棒グラフの描画の一例として、g_box_2D 関数を用いて以下のように描画する方法が考えられる。

　g_box_2D(0.2+i, 0.8+i, 0.0, prob[i], G_YES, G_YES)

　これは、i+1 の目の確率を描画する棒グラフになっている。
　1,2番目の引数は四角形の左端、右端になっているが、中央が i になっている。
　3,4番目の引数は四角形の下端、上端であり、確率を表示したいので上端が prob[i] となっている。
　こうすることで、隣の棒グラフと少し隙間をあけた棒グラフが作成できる。
　あとは、for 文で i をサイコロの目の分だけ繰り返せば、出た目の確率の棒グラフが作成できる。

　下図のような描画を行うためには、g_def_scale_2D 関数で定義する自由座標系の領域をどのようにすれば良いか、 よく考えてみよう。
　１の目と６の目の出現回数の棒グラフのx座標をそれぞれ考えてみれば、x座標の範囲はわかりそう。
　y座標は、下のグラフの範囲で問題なさそう（サイコロを振る回数Nが少ないと、1/3を上回ることは十分あり得るが）。

課題の提出

「課題」で作成したプログラムを提出してください。

ただし、コメント文として、

学生番号、名前、プログラムの説明

を書くこと。 ファイル名は、05-rep.c として、ファイル単体でコンパイルできるようにすること。

提出締め切り：　2024年10月21日19時

中間レポート課題

フラクタル図形の一種であるコッホ曲線を表示するプログラム、あるいはフラクタル図形を利用したオリジナルの CG(コンピュータグラフィックス)を表示するプログラムを、GLSC3Dを用いて作成せよ。 描画には必ず GLSC3D を用いること（旧GLSCの使用は認めない）。

フラクタル図形を利用したオリジナルのCGについては、手の込んだCGほど高く評価する。
（例年、どこかのサイトに載っている非常に単純なフラクタル図形を描画してそのまま提出する人がいるが、 そのようなものはかなり低い評価になる）
コッホ曲線にオリジナルの要素を加えることも、加点要素となる。

また、「条件文」、「繰り返し文」、「scanfによる入力」、「関数」、「配列」の「全て」を用いるプログラムにすること。
（関数の再帰呼び出しは必ずしも使う必要はないが、正確に使えていれば加点要素とする。）

提出されたファイル単体で、ccg コマンドにより正常にコンパイルでき、実行できるものに限る。 提出ファイル単体でコンパイルできない場合は、大幅に評価は下がる。

ソースプログラムには、作成者以外の人がソースプログラムを見た場合にプログラム動作が容易にわかるよう、 適宜コメント文にて説明を加えること。 コメントがない、あるいは十分でない場合には、それに応じて評価は下がる。

アニメーション効果を入れる等（アニメーションは必須ではない）、各自工夫すること。 当然、良く工夫されている方が評価は高くなる。 また、パラメータをプログラム実行時に入力させる場合には、 コメント文にオススメのパラメータの値を表記しておくこと。

ソースプログラムの先頭部分にコメント文として、 名前、学籍番号、プログラムの概要、プログラムで工夫したこと、参考文献（書籍名、URL）等を書くこと。 例えば、以下のように記載。

// 名前：明治太郎
// 学籍番号：123456
// このプログラムは、コッホ曲線を参考に以下の様なルールで作成した
// フラクタル図形を表示します。
// ・・・描画ルール等・・・
// 参考文献１にフラクタル図形と海岸線との関係が載っていたので、
// 図形が海岸線に見えるように工夫しました。
// また同時に図形のフラクタル次元を測り、それも表示する様にしました。
// （わかりやすく説明を書いて下さい）
// 参考文献：
// 1. カオスとフラクタル、山口昌哉、ちくま学芸文庫(2010)
// 2. 眠る猫と世界の形（動画）、サイエンスチャンネル、
// 　https://sciencechannel.jst.go.jp/B033305/detail/B033305001.html

#include <glsc3d_3.h>
#include <stdio.h>
#include <math.h>
・・・・・・（続く）・・・・・


フラクタルの概念については、以下の資料等が参考になるでしょう。

注意：
当然のことながら、レポートのプログラムは自分で作成したものを提出すること。 友達や教員、TAの方々に分からないことを聞いたり、相談することはもちろん構わないが、 web サイトの内容含め他人の制作物の丸写し（あるいは、それと同等と見なせるもの）は厳禁！ レポートにおける他人の丸写しやそれに類する行為（剽窃＆盗用）は、 テストで言えばカンニング行為に当たるので、 見つけた場合にはカンニングと同等の厳しい処分を行う。（実質上、単位取得は不可と思ってください）
どうしても分からず、手伝ってもらった部分があれば、正直に記載すること。 記載なしに同等と見なせる内容が見つかった場合には、両者ともに厳しい処分とします （どちらが写したか分からないから）。
chatGPT等の生成AIを利用した場合には、利用した箇所を明示すること！ 記載がなく疑わしい場合や理解せずに丸写ししていると考えられる場合には、書かれたコメント内容で判断します。 理解せずに使用していると判断した場合には、カンニングと同様の処分を行います。
それらを防ぐためにも、内容をきちんと理解した上で、自分の言葉を用いて十分に説明を記載しておくこと。


Oh-o! Meiji のレポートシステムを利用して、11月24日（日）23時までに、 ファイル名を MidRep.c として「中間レポート課題」に提出してください。 11月26日（日）23時より遅れると、どのような事情があっても提出できませんので、余裕を持って提出して下さい。


中間レポートについて、採点基準は以下の通りです。


中間レポート課題を35点満点、学期末に出題予定の期末レポート課題を50点満点、その他毎回のレポート課題の合計を15点満点として採点します。

提出締め切り：2024年11月24日（日）23時

コッホ曲線

コッホ曲線とは、以下の操作を繰り返すことにより得られる図形である。

１. 直線を引く

２. 直線を３等分する

３. 直線を等分した２点を頂点とする正三角形をつくる

４. 出来上がった各線分について２、３を繰り返す

上記の操作を適当な回数（十回程度）繰り返して得られる図形を描くGLSC3Dのプログラムを作成せよ。 以下に、そのようなプログラムの実行例をあげる。

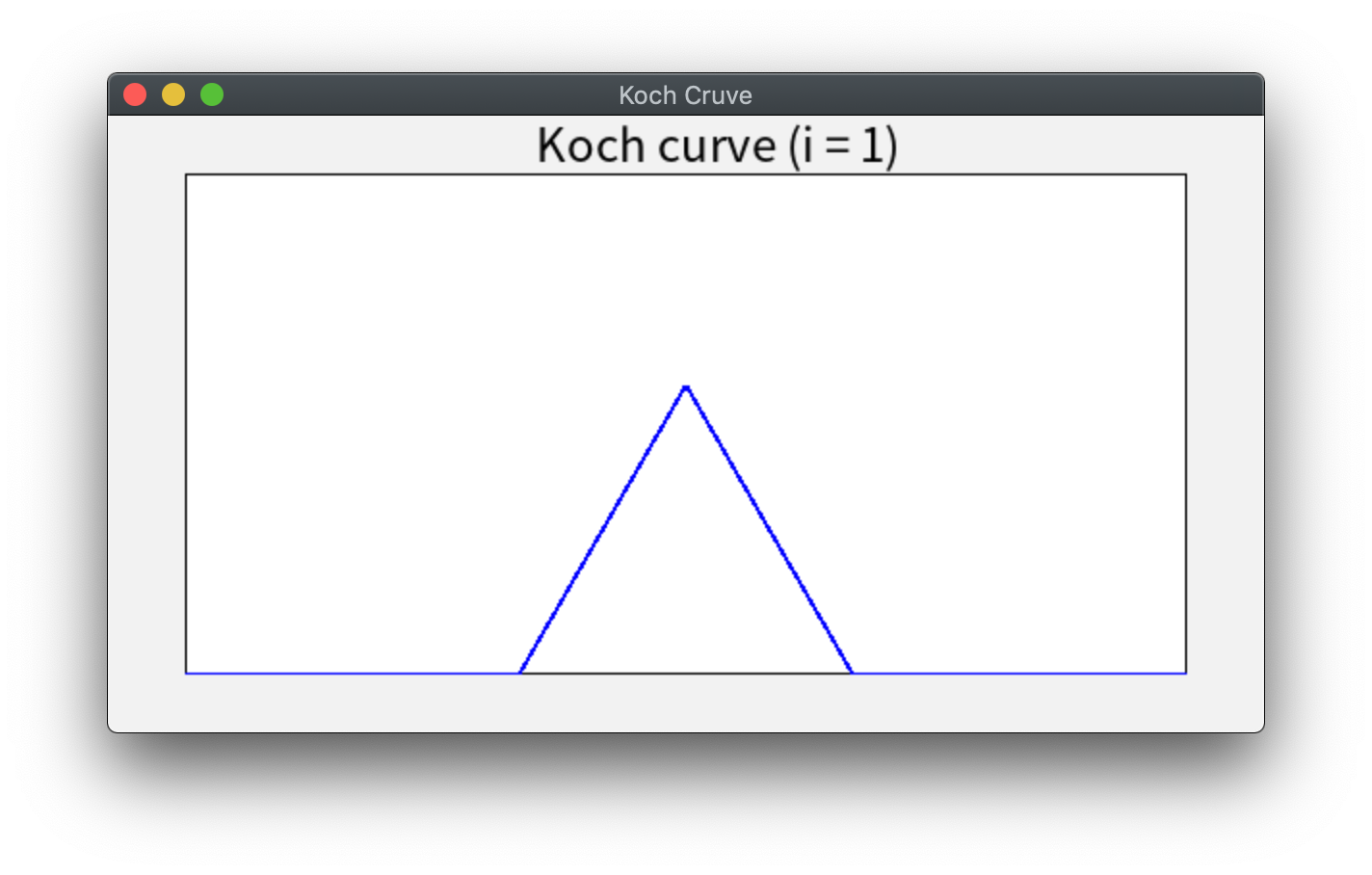
青い直線を３等分し、等分した２点で正三角形を作ったところ。４つの線分にわかれた。

　

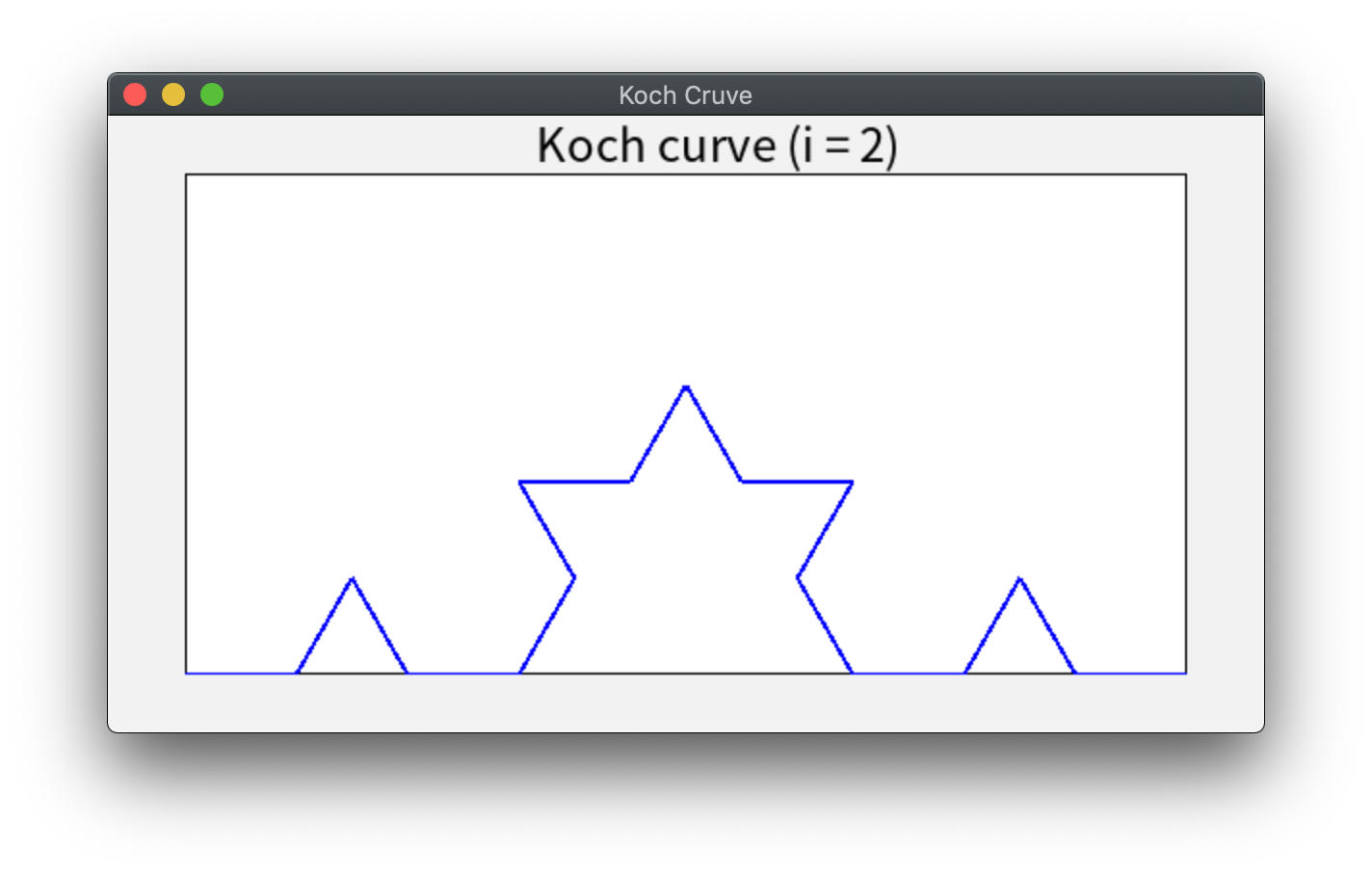
上で得られた４つの線分に対して、同様の操作（それぞれの線分を３等分し、等分した２点で正三角形を作る）を経て得られた図形。 １６の線分により構成される図形となる。 次も同様に、その１６の線分全てについて同様の操作を行う。 以下、これを繰り返していく。

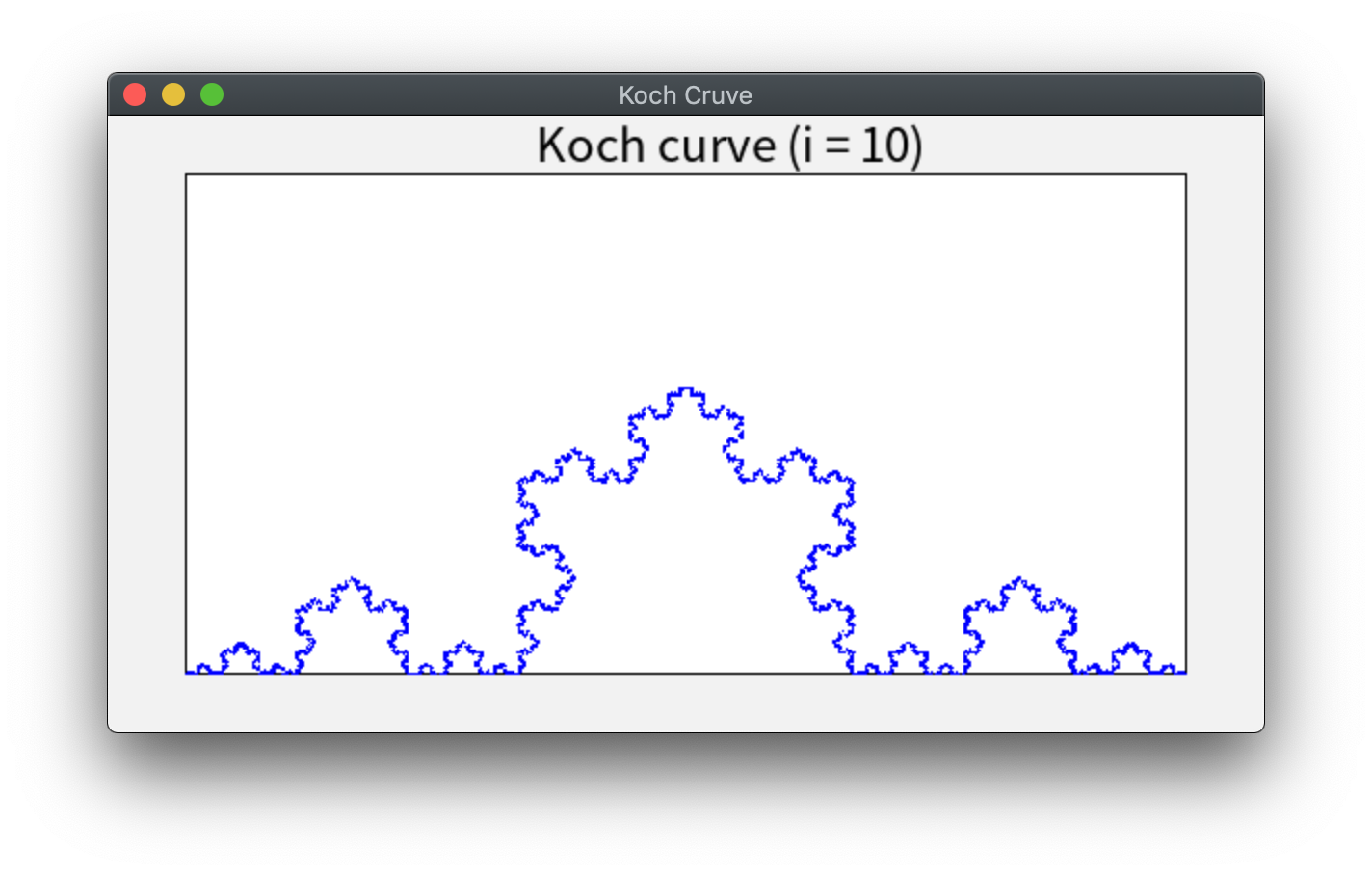
上記手続きを１０回繰り返した後得られた図形。実際には、細かすぎるため5回目くらいから見た目はほとんど変化していない。 10回繰り返した場合、線分は 4^10 = 1,048,576 本になるので、 さらに繰り返しが増えると描画にかなりの時間を要する。

関数の再帰呼び出しを使えば簡単だが、関数の再帰呼び出しを使わなくてもできるので、関数の再帰呼び出しの知識が無くてもよい。

参考：関数の再帰呼び出し

関数の再帰呼び出しを使うと、プログラムの記述が簡潔になる場合があります （ただし、簡潔になることが効率的なこととは限らないことに注意）。 例えば、最大公約数を求めるユークリッドの互除法のアルゴリズムやフラクタル画像の描画などは、 再帰呼び出しを使うとスマートに記述できます。

ユークリッドの互除法（復習）

二つの整数の最大公約数を求める問題を考えます。 最大公約数とは共通の約数のうち最大なもので、２個の整数m, n の最大公約数とは、 m = ad, n = bd を満たす整数 a,b が存在するような最大の整数 d です。 これを、gcd(m, n) と書く事にしましょう。(gcd は Greatest Common Divisor の略)

さて、負でない整数 x, y の最大公約数は、x を y で割ったあまりを r としたとき、

gcd(x, y) = gcd(y, r)

である事を用いて効率よく求める事ができ、この方法は「ユークリッドの互除法」と呼ばれています。 上記を書き換えると、

gcd(x, y) = gcd(y, x mod y)

となります。つまり、まとめると、ユークリッドの互除法は次のようになります。

　gcd(x, y) = gcd(y, x mod y) 　　(y != 0 のとき）

　gcd(x, y) = x 　　　　　　　(y == 0 のとき）

これを繰り返せば、最大公約数が求まります。 具体例を見てましょう。 以後、mod を % と書きます（Ｃ言語風）。

gcd(12707, 12319) = gcd(12319, 12707%12319) = gcd(12319, 388)

-->gcd(12319, 388) = gcd(388, 12319%388) = gcd(388, 291)

-->gcd(388, 291) = gcd(291, 388%291) = gcd(291, 97)

-->gcd(291, 97) = gcd(97, 291%97) = gcd(97, 0)

-->gcd(97, 0) = 97

よって、12707 と 12319 の最大公約数は 97 である事が求まります。

さて、このアルゴリズムをC言語で実装しましょう。

最大公約数を求める関数 gcd（その１）

これまでの知識を用いて、gcd(x, y)を求める関数 gcd を作りましょう。 mod は C言語では % と書きますので次のようになります。

int gcd(int x, int y)
{
　int t;
　while(y != 0)
　{
　 　　t = x % y;
　 　　x = y;
　 　　y = t;
　}
　return x;
}

最大公約数を求める関数 gcd（その２）

関数の再帰呼び出しを用いるとよりスマートにかけます。

int gcd(int x, int y)
{
　if(y == 0)　{
　 　　return x;
　}　else　{
　 　　return gcd(y, x%y);
　}
}

gcd その２ の動作を実際に見ることで、関数の再帰呼び出しを理解しましょう。 下の gcd 関数の定義の部分には、その動作を見る為に printf 文を追加しています。 下のプログラムをコピペして、実際に動作を確認してみましょう。 

#include <stdio.h>
int gcd(int x, int y);
int main()
  {
    printf("gcd(12707, 12319) =%d\n", gcd(12707, 12319) );
    return 0;
  }
     
  int gcd(int x, int y)
  {
    printf("-->gcd(%d, %d)\n", x, y);
     　
    if(y == 0) {
      return x;
    } else {
      return gcd(y, x%y);
    }
  }

上記プログラムを実行すると以下の様な出力が得られます。

-->gcd(12707, 12319)
-->gcd(12319, 388)
-->gcd(388, 291)
-->gcd(291, 97)
-->gcd(97, 0)
gcd(12707, 12319)=97

関数 gcd の定義の中に gcd 自身が入っているので、関数の再帰呼び出しとよばれます。 プログラムの動作を実際に目で追って、よく理解してください。 先のユークリッドの互除法の説明部分そのままにプログラミングされていて、そのまま動作する事を確認してください。 はじめは分かりにくいですが、よく見る事で理解できますし、それ以外理解できるようになる方法はありません。

また、３個の負でない整数の最大公約数は gcd(a, b, c) = gcd(gcd(a, b), c) として求められます。 ４個以上も同様です。

戻る