第６回　C言語による現象のシミュレーション２ (2024年11月11日)

今日の内容

• 渋滞現象の数理モデル
• 交通流モデルのプログラム
• GLSC3Dによる交通流モデルの可視化

渋滞現象の数理モデル

今回は渋滞現象の数理モデルのシミュレーションを行うプログラムを作成します。
そのために、まずはどのようにして渋滞現象を数理モデル化するかについて考えてみましょう。 ここでは、車の渋滞について考えていきます。

まず、渋滞はどのような場合に起こるのでしょうか？ 当然のことながら、車が多い時に渋滞は発生します（連休中の高速道路など）。
ですが、もしそれぞれの車が一定の車間距離を維持したまま同じ速度で走り続ける事ができれば、渋滞は発生しないのではないでしょうか？ （例えば、自動運転技術が発展すれば渋滞は無くなるのではないか）

しかし、答えはNOです。
たとえ、自動運転技術が発達して自動的に一定の車間距離のまま同じ速度で走り続ける事ができるようになったとしても、 渋滞を無くす事はできません。

下の動画では、プロのレーシングドライバーに依頼して、一定の車間距離を保ったまま円周上のサーキットを走ってもらっていますが、 それでも渋滞は発生しています。
Shockwave traffic jams recreated for first time

たとえ、これが人間ではなく自動運転になったっとしても、ある一定の車両密度を超えると渋滞は必ず発生してしまいます。
このように、ある量が変化することにより集団の状態がガラッと変わってしまう現象を、「相転移」と呼びます。
相転移の代表例は、物質の状態変化、つまり温度や圧力の変化により水が氷や水蒸気に変化する現象です。
渋滞現象も数理モデルを通してみると、水（液体）から氷（固体）への変化と同様に、 スムーズに車が流れている状態から渋滞状態への変化が起こっていると捉える事ができます。

渋滞状態への相転移は、「交通流量」を調べることで理解することができます。 交通流量とは、ある地点を一定時間内に通過する車の数のことです。
下の図では、車両密度（車の台数と考えて良い）と交通流量の変化をプロットしています。
車の流れがスムーズな状態では、車の台数が増えるほど交通流量が増加します。
一方、渋滞状態では車の台数が増えるほど交通流量が減少しています。 これは、渋滞が起こることにより車が増えれば増えるほど車の移動速度が下がるので、 車の台数が増えているにもかかわらず一定区間を通過する車の量が減ってしまうためです。

それでは、この車の渋滞現象をどのように数理モデル化すれば良いでしょうか？
ここでは簡単のために、1車線で1方通行の道路を考えてみます。 ただし、この道路の右端と左端はつながっている（あるいは円周状になっている）とします。

交通流の数理モデル化の最も簡単な例として、セル・オートマトンを用いた数理モデル化があります。 セル・オートマトンは、空間を格子状に分割し近隣の格子（セル）との相互作用により、状態を変化させていくモデルです。 2次元のセル・オートマトンの代表例としては、Life Game があります。
交通流の数理モデルでは、１次元のセル・オートマトンを使うのが一般的です。 そこでここからは、１次元のセル・オートマトンを用いて交通渋滞の数理モデル化を行っていきます。

Rule 240 モデル

まずは、最もシンプルなモデルを考えてみましょう。
1次元の格子を道路と見立てて、そこに車を配置していきます。下図では、車を円で表しています。
車は一方行に進んでいくので、１ステップごとに右に進んでいきます。
このモデルでは、自分の目の前に車があるかないかにかかわらず、前に進んでいくことにします。 これを模式的に描いたのが下図になります。

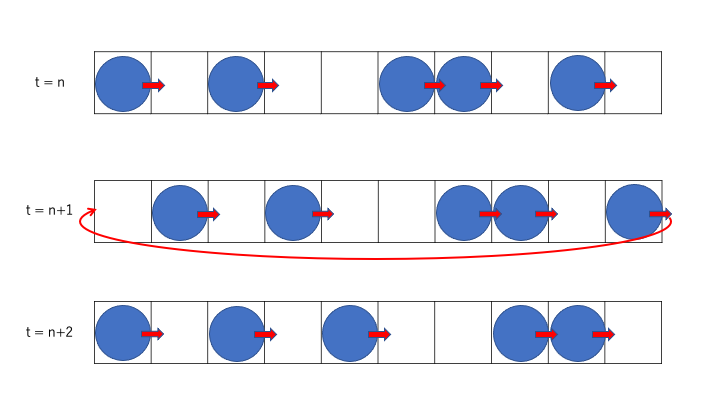
このモデルは、ルール240と呼ばれるモデルになっています。
(１次元のセル・オートマトン は最隣接の格子との相互作用のルールの決め方によって256種類のモデルがあり、その中の240番のルールを持つモデルという意味)

このモデルでは、前方の車の有無にかかわらず常に前方向に進んでいってしまうため、どんなに車を多く配置しても渋滞は起こりません。
つまり、どんな状況でも常に一定の車間距離を保ち同じ速度で進み続けられるモデルになっています。
もちろん、これでは現実的な交通流のモデルとは言い難いでしょう。

Rule 184 モデル

先ほどのモデルの問題点は、前方に車がいるにもかかわらず前に進み続けることでした。
そこで、前に車がいる場合には一旦止まるというルールを課してみましょう。
これを模式的に描いたのが下図になります。

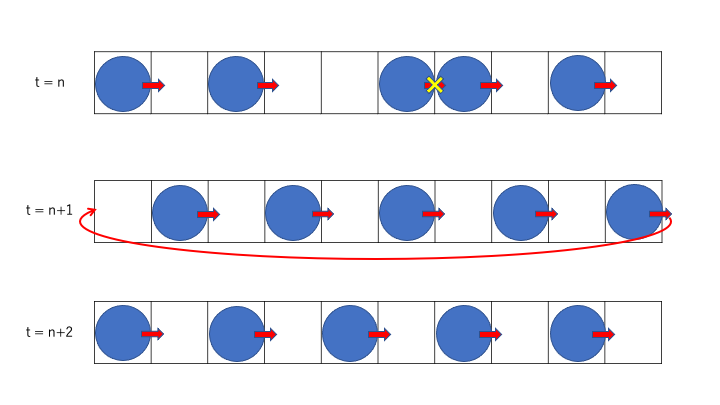
このモデルは、ルール184と呼ばれるモデルになっています。
直前のセルが空いている場合には前に進んで行きますが、直前のセルに車がいる場合には停止する、 つまり次のステップでも同じセルにいたままになります。
もし前に車がいなくなれば、次のステップからまた前に進んでいきます。

このモデルでは、直前のセルに車がある限り前に進むことができず、 ある程度車の台数が多くなってしまうと停車する車が現れる、つまり渋滞が発生することになります。
一般的には、このモデルが最もシンプルな交通流のモデルとして扱われています。

Slow to Start モデル

さらにもう少し現実的な車の挙動を考えてみましょう
車は一旦停車して再発進する際に、いきなりトップスピードになるわけではありません。 どんな物体にも「慣性」があるので、再発進の際には徐々にスピードを上げていくと考えるのがより現実的です。
しかし、簡単なセル・オートマトンモデルではスピードの変化を考慮することは難しいので、 ここでは「一旦停止すると再発進までの準備に時間がかかる」としてみましょう。
すなわち、「車が停止状態になると前方が空いてもすぐ発進できず、進行する状態までの移行時間が存在する」というモデルを考えることにします。 これを模式的に描いたのが下図になります。

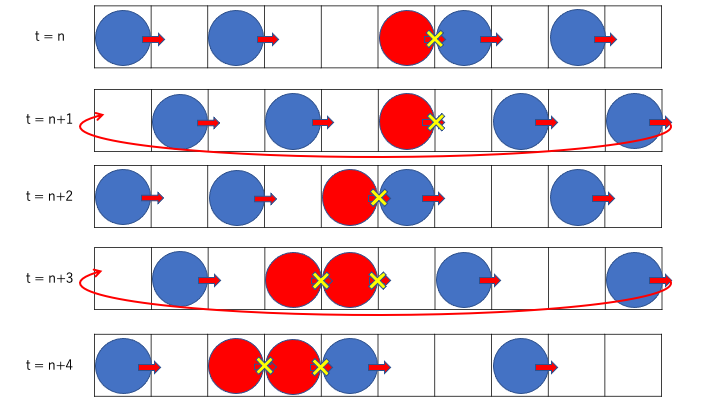
このモデルは、Slow to Startと呼ばれるモデルになっています。
上の２つのモデルと異なり、車は「停止（赤色）」と「進行（青色）」の ２つの状態をとることになります。

進行状態の車の直前に車が存在すると、動いてきた車は進行状態から停止状態に移行します。
停止状態の車は前方に車がある限りは停止状態のままです。
前方の車がなくなると、停止状態の車は次のステップで位置が変わらないまま進行状態に移行します（これが発進準備）。
進行状態に移行したら、次のステップからは前に進むことができます（もちろん前方に車がなければ）

このモデルでは、慣性によりスムーズに車が発進できなくなることで、上の２つのモデルよりもより渋滞が発生しやすいモデルになっています。
また、このモデルを用いて車両密度と交通流量のグラフを描くと、実際の高速道路におけるデータで現れる特徴（メタ安定性）が再現できることも知られています。

交通流モデルのプログラム

まずはGLSC3Dでの可視化は考えずに、上記のモデルのアルゴリズムを考えた上でプログラムを作成してみましょう。

ルール240モデルのアウトライン

• 道路を1次元配列で表現し、配列の要素は自動車がある・なしの二つの状態（1:車あり　0:車なし）
• 道路の長さは例えば100とする（例えば、int r[100];）
• 単一レーンの道路を考え、自動車は左から右に進むとする
• 道路上には自動車が一定数存在する状態を考える
• 自動車は各時間右方向に必ず1ます進むとする
• 離散的な時間を考え、現在の状態から次の状態へ変化する（自動車が動く）と考える

もう少し具体的には、以下のような疑似コードとなります。

これを踏まえて、実際にプログラムを書いてみると例えば以下のようになります。

#include <stdio.h>
#include <stdlib.h>

#define L (100)  // 道路の長さ
#define RN (rand()/(double)RAND_MAX)  // 0.0〜1.0の一様乱数を発生
#define TH (0.4)   // 自動車の密度（どれくらいの確率で配置するか）
#define TMAX (30)  // 時間繰り返しの回数

int main(){
    int i, t;
    int r1[L], r2[L];

    // 乱数の種を設定（毎回同じ乱数列が生成）
    srand(1);

    // 道路状況の初期化、自動車は TH の確率で置く
    for(i = 0; i < L; i++) {

        // 乱数がTH（配置確率、密度）より小さければ自動車配置
        if(RN < TH) {
            r1[i] = 1;
        // それ以外は、自動車なし
        } else {
            r1[i] = 0;
        }
        // 更新処理用の配列の初期化
        r2[i] = 0;
    }

    // 初期の道路状況の表示
    // 車がなければ " "(空白)を表示、車があれば "o" を表示
    for(i = 0; i < L ; i++) {
        if(r1[i] == 0) { printf(" "); }
        else { printf("o"); }
    }
    printf("\n");


    // 時刻TMAXまで繰り返して、道路状況を更新
    for(t = 1; t < TMAX; t++) {

      
        // 自動車を右方向に移動、ただし円環状道路（端まで行ったら最初に戻る道路）を考える
        for(i = 0; i < L; i++) {
            r2[(i + 1)%L] = r1[i];
        }
        

        // 道路状況の更新＆更新処理用の配列の初期化
        for(i = 0; i < L; i++) {
            r1[i] = r2[i];
            r2[i] = 0;
        }

        // 現在の道路状況の表示
        // 車がなければ " "(空白)を表示、車があれば "o" を表示
        for(i = 0; i < L ; i++) {
            if(r1[i] == 0) { printf(" "); }
            else { printf("o"); }
        }
        printf("\n");

    }

  
    return 0;
}

上記のプログラムで少しトリッキーなのは、

r1[(i + 1)%L]

という表記でしょう。
これは一つ前方の車の状態を表すものですが、(i+1)%L としているのは、一番右端まで行くと次は左端に移動するためです。
これは、r1[L-1] から r1[0] への移動を表しており、% L（Lで割ったあまり）の演算を行うことで if 文を利用せずに目的の位置の状態にアクセスすることができます。

ルール184モデルのアウトライン

基本的には、ルール240 のプログラムをちょっとだけ修正するだけ。 ルール240 との違う部分だけ書くと、以下のようになります。

• 車がある場所を調べて、一つ前方に車がなければ前に移動、車があればその場にとどまる

現在の車がある場所を調べるには、if 文で r1[i] の値により判断すれば良い。
その上で、一つ前の状態 r1[(i+1)%L]を調べて、その状態により r2 に代入すれば良い。
ただし、前方に車のあるなしで車が移動するか否かが変わるということは、r2 のどこに代入するかが変わってくることに注意。

Slow to Start モデルのアウトライン

上記の2つのモデルと比べると、変わるところも少しあるが大まかな方針は以下の通り。

• 配列の要素は三つの状態（0:車なし　1:停止　2:進行）
• 初期配置は、停止状態の車を配置
• 進行状態の車は、一つ前方に車がなければ前に移動、車があれば停止状態に移行してその場にとどまる
• 停止状態の車は、一つ前方に車がなければその場にとどまったまま進行状態に移行、車があればその場で停止状態のまま

車の場所の移動だけでなく、車の状態の変化もきちんと考えなければいけないことに注意。

GLSC3Dによる交通流モデルの可視化

上記のモデルをGLSC3Dで可視化するには、以下のようなプログラムが考えられます（一部はあえて書いていないので、自分で追加する）。

車の描画には、g_marker_2D() 関数を用いています。
g_marker_2D() 関数は、マーカーを表示させたい位置の自由座標系における座標を与えるだけで良いです。
大きさを変えたい場合には g_marker_size() 関数、マーカーの種類（形）を変えたい場合には g_marker_type() 関数、 色を変えるには g_maker_color() 関数を使います。
詳しくは、マニュアルをみてみましょう。

#include <stdio.h>
#include <stdlib.h>
#include <glsc3d_3.h>

#define L (100)  // 道路の長さ
#define RN (rand()/(double)RAND_MAX)  // 0.0〜1.0の一様乱数を発生
#define TH (0.54)   // 自動車の密度（どれくらいの確率で配置するか）
#define TMAX (300)  // 時間繰り返しの回数

int main(){
    int i, t;
    int r1[L], r2[L];

    // 乱数の種を設定（毎回同じ乱数列が生成）
    srand(10);

    // 道路状況の初期化、自動車は TH の確率で置く
    for(i = 0; i < L; i++) {

        // 乱数がTH（配置確率、密度）より小さければ自動車配置
        if(RN < TH) {
            r1[i] = 1;
        // それ以外は、自動車なし
        } else {
            r1[i] = 0;
        }
        // 更新処理用の配列の初期化
        r2[i] = 0;
    }


    // GLSC3Dの初期化
    g_enable_highdpi();
    g_init("Traffic Jam", 1250, 200);
    // 自由座標系の定義
    g_def_scale_2D(1, 0.0, L, 0.0, 1.0, 25.0, 100.0, 1200.0, 30.0);
    g_sel_scale(1);
    g_cls();

    // 外枠の描画
    /*
    ここに for 文使って、g_box_2Dで格子をL個描く
    */

    // 現在の道路状況の表示
    // 車がなければ " "(空白)を表示、車があれば "o" を表示
    // 車があればg_marker_2Dで表示
    //（このコードには書いてないので自分で追加、必要に応じてマーカーの大きさや色を変更）

    for(i = 0; i < L ; i++) {
        if(r1[i] == 0) {
            printf(" ");
        } else {
            printf("o");
        }
    }
    printf("\n");

    // 画面への描画
    g_finish();
    // 一定時間停止
    g_sleep(1.0);

    // 時刻TMAXまで繰り返して、道路状況を更新
    for(t = 1; t < TMAX; t++) {

        // 自動車を右方向に移動、ただし円環状道路（端まで行ったら最初に戻る道路）を考える
        // もし一つ前に車があれば、移動できない（このコードには書いてないので、自分で追加）
        for(i = 0; i < L; i++) {
            r2[(i + 1)%L] = r1[i];
        }

        // 道路状況の更新＆更新処理用の配列の初期化
        for(i = 0; i < L; i++) {
            r1[i] = r2[i];
            r2[i] = 0;
        }

        // 画面の消去
        g_cls();

        // 外枠の描画
        /*
        ここに for 文使って、g_box_2Dで格子をL個描く
        */

        // 現在の道路状況の表示
        // 車がなければ " "(空白)を表示、車があれば "o" を表示
        // 車があればg_marker_2Dで表示
        //（このコードには書いてないので自分で追加、必要に応じてマーカーの大きさや色を変更）
    

        for(i = 0; i < L ; i++) {
            if(r1[i] == 0) {
                printf(" ");
            } else {
                printf("o");
            }
        }
        printf("\n");

        // 画面への描画
        g_finish();
        // 一定時間停止
        g_sleep(0.3);
    }

  
    return 0;
}

◎課題

課題の提出

課題で作成したプログラムを提出してください。 ただし、コメント文として

学生番号、名前、プログラムの説明

を書く事。

ファイル名は、06-rep.c として、 ファイル単体でコンパイルできるようにすること。

課題の提出場所の間違いに注意！！

提出締め切り：　2024年11月11日19時

戻る