第9回 新しい関数の定義(def)

これまで扱ってきたのは短いサンプルプログラムばかりで、一気に書け、一目で理解できる簡単なものだった。実行の流れも、条件分岐や繰り返しはあっても、基本的には上から下への一方通行だった。
だが、この「プログラミング入門」も後半にさしかかり、より複雑で長いプログラムを扱うことになる。そもそも皆さんがプログラミングを学ぶのは、サンプルではなく、自分のやりたい（それなりに複雑な）ことをプログラムで表現し、自在にコンピュータを操りたいからであろう。
何を言いたいのかといえば、長いプログラムには、短いプログラムには必要がない、全体をどう組み立てるかという構成論が必要になるということである。Pythonを含め、主要プログラミング言語はどれも、大規模なプログラムを整然と、わかりやすく構成する仕組みを備えている。

この回の内容

構造的プログラミングとは

時代とともにプログラムの規模と複雑さは指数関数的に増大し、それとともに新しい構成論のパラダイムが提唱されてきた。ほぼ登場順に、

  1. 構造的プログラミング
  2. オブジェクト指向プログラミング
  3. 論理プログラミング
  4. デザインパターン
  5. AI駆動プログラミング
などである。そして主要なプログラミング言語は、いくつかのパラダイムを取り入れて開発されている。
Python言語の仕様も、1と2のパラダイムを踏まえている。今回は、1の構造的プログラミングと、それを実現する「関数」と「モジュール」について学ぶ。これにより、より長く複雑なプログラムを設計したり、読解する「プログラミング応用」への準備態勢ができるはずだ。
2のオブジェクト指向プログラミングについては、残念ながら「入門」で扱う余裕がないが、それを実現する「クラス」と「オブジェクト」は、GUIプログラミングなどに欠かせない仕組みである。
5のAI駆動プログラミングについては、第14回の授業で片鱗に触れる予定である。

関数の定義と呼び出し

「関数」と聞くと、高校数学の授業を思い出して身構える人がいるかもしれないが、プログラミングで使う「関数」はさほど難しいものではない。「一定の計算をして答を返す計算パッケージ」※1という程度のものだ。

1　たとえば自動販売機は、一定の金額を入れて同じボタンを押せば（入力・引数）、必ず同じ「午後の紅茶」が出てくる（出力・値）。そして「午後の紅茶」を買うのに自動販売機のしくみを知る必要はない（詳細の隠蔽）。いまはそんなイメージで十分だ。

この授業ではPythonの関数をすでに使っている。

input()※2
ユーザから入力文字列を得る
print()
変数の内容や文字列を出力する
int()
数値を整数化する
sqrt()
平方根を求める
これらの関数は、引数を与えて呼び出せば、（自動販売機のように）いつも一定の結果（値）を返してくれる。それぞれの計算の詳細は隠されており、私たちも値を受け取れればそれで十分だ。その方がプログラムもはるかに読みやすくなる。つまり関数は、繰り返し利用する計算アルゴリズムをカプセル化してくれる。

2　関数名の後の( )は、関数にデータを渡すインタフェースだ。また、変数に代入されているのは、関数が返したデータである。これらをそれぞれ、関数の引数、値（戻り値）という。Pythonの関数は複数の引数を取れ、複数の値を返せる。

ところで、上に挙げた関数の詳細（計算内容）がプログラム中に書かれていないのは、Python処理系であらかじめ定義されたシステム関数だからだ。システム関数は多数あり、言語本体やシステム・モジュール（sys、os、mathなど）で定義されている。どのモジュールにどんな関数があるかは言語リファレンスを参照すればわかる。すでに用意されている関数と同じ処理を、自分で書くのは時間と思考の無駄なので、普段から言語リファレンスには目を通しておくとよい。
今回はシステム関数ではなく、自分で書いたプログラムの一部分を新たなユーザ関数として定義する方法を学ぶ。
平方根sqrt( )ほどではなくても、自分で書いたプログラム中にも、別の機会に再利用したくなる部分、つまり汎用性のある部分は必ず存在する。それに名前をつけ、データを受け渡すための引数と値のインタフェースを定義して、他のプログラムから呼び出せるようにすれば、一度書いたプログラムがシステム関数と同様に何度でも再利用できるので、その分の労力を新たな仕事に振り向けられる。

ヘロンの公式

汎用性のある計算と聞いて、最初に思いつくのは数学の公式だろう。3角形の面積は、もちろん底辺と、底辺に垂直に計った高さが分かれば求まるが、実際の測量現場では、直角を図ったり、垂線を立てる作業が困難な場合もある（池あり、山あり）。そこで実際には3辺の長さを測り、図9-1に示すヘロン※3の公式で計算する。

図9-1: ヘロンの公式

3　ヘロンは紀元1世紀にアレクサンドリアに住んでいたギリシャ人学者。エラトステネスといい、ヘロンといい、あのピタゴラスといい、まことに「古代ギリシャの数学力は（哲学力も）世界一イイイィィィ!!」なのだった。

このプログラムはもちろん、「飲み会の勘定清算」プログラムと同様、関数を定義しないでも書ける。しかしそれでは「ヘロンの公式」自体が、分かりやすい形でユニット化されないし、他のプログラムから呼び出すインタフェースを定義して再利用することもできない。
それらを解決するために、

したのがリスト9-1である。

リスト9-1: heron.ipynb

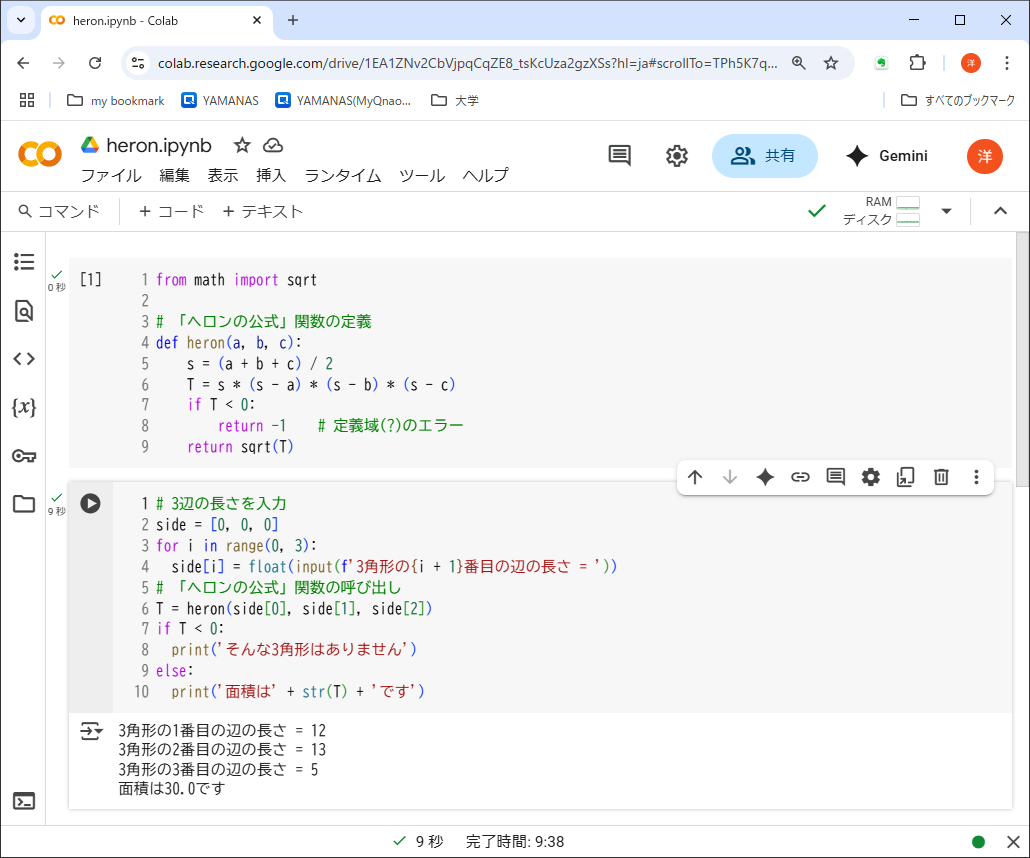
最初のコードセルで、関数heron(a, b, c)を定義することで、公式を使って3角形の面積を計算する部分と、それを利用する部分が分離され、全体の見通しがはるかによくなった。def構文は複雑に見えるかもしれないが、これでも同時に変数の型を宣言しなくてはならない主流言語（C系、javaなど）に比べればかなり簡素だ。
関数heron()の定義は、

であると明確に表現されている。
つぎのコードセルは、ユーザから3角形の辺の長さを受け取り、関数heron()を呼び出す利用側のプログラムである。heron()からエラーコード(-1)が返ってきた場合の「後始末」も、利用側の役割だ。
変数名には注意！ heron()関数内で使われている変数a, b, cは、まだ特定の値をもっていない「仮引数」である。一方、呼び出し側で使っているside[0], side[1], side[2]は、ユーザから受け取った具体的な値を格納した「実引数」である。関数が呼ばれると、仮引数に実引数（の値）が暗黙裡に代入される。
構造化プログラミングにおいて、関数はプログラムを組み立てる基本的なブロックである。関数(function)とは、このブロックがもつ、入力値を出力値に変換する機能に由来する名前だが、言語によっては同じものを、プログラムの処理手順（routine）の一部を切り出したものという意味でサブルーチン(subroutine)と呼ぶ。

2次方程式の解

新たなユーザ関数を定義できる便利さを実感してもらうために、もう1つの例を挙げよう。中学で習った2次方程式の解の公式だ。皆さんはつい最近だから記憶も鮮明だろうけれど、私にとっては半世紀前(!)なので、思い出すのにちょっと苦労した。つまりこうだ。

図9-2: 2次方程式の解の公式

「-b」の後の「±」によって、実数解が1つだったり2つだったりするんでしたよね。実は図から読み取れないこともあり、「√」内が負になることが、実数解が存在しない条件である。Pythonの関数は複数の値を返せるので、2つの解を返すのは簡単だが、「実数解がない」状態を呼び出し側に伝えるにはどうしたらよいだろう？※4
Pythonらしい解決法は、2つの解に続けて3つめの「解有り」という真偽値を返すことだ。Trueならば実数解があることを、Falseならば実数解はないことを示す。

4　解1、解2に特別な値を返して「実数解がない」というエラーコードを表す、heron()と同じ手は使えない。なぜならどのような2つの値でも、それを解とする2次方程式は存在するからである。また、どのようなa, b, cに対しても複素数解なら必ず存在する。

3つめの値「解有り」によって、呼び出し側では異なる処理に分岐できる。リスト9-2は実数解がある場合。

リスト9-2: 2次方程式の解(quadratic.ipynb)

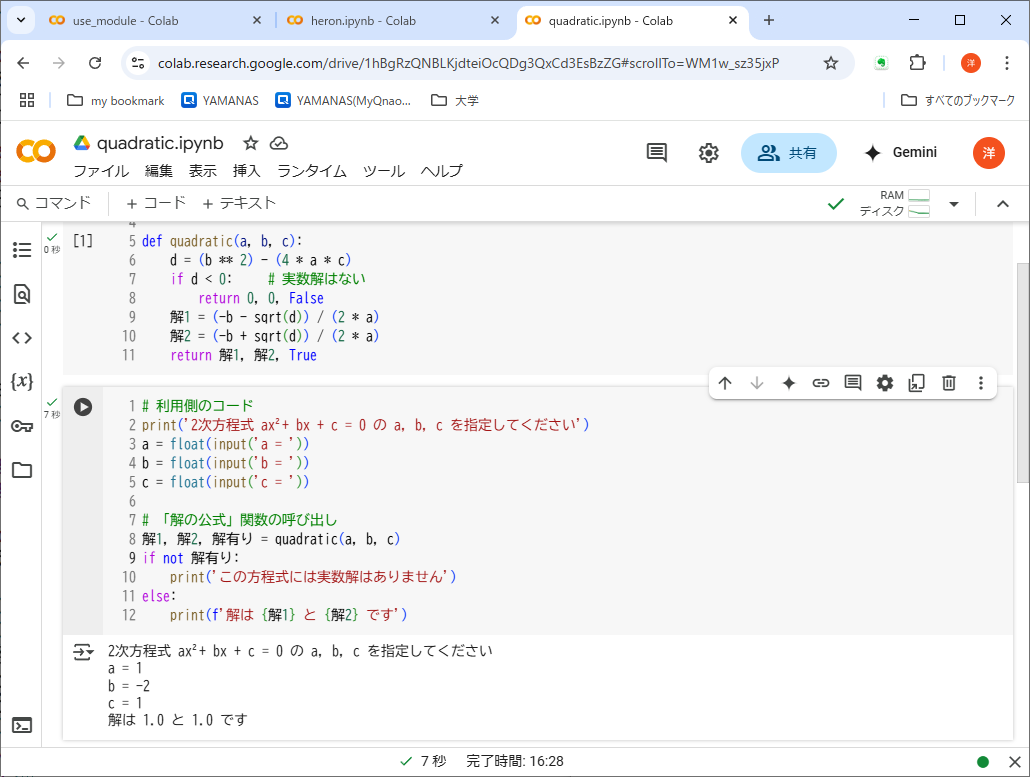
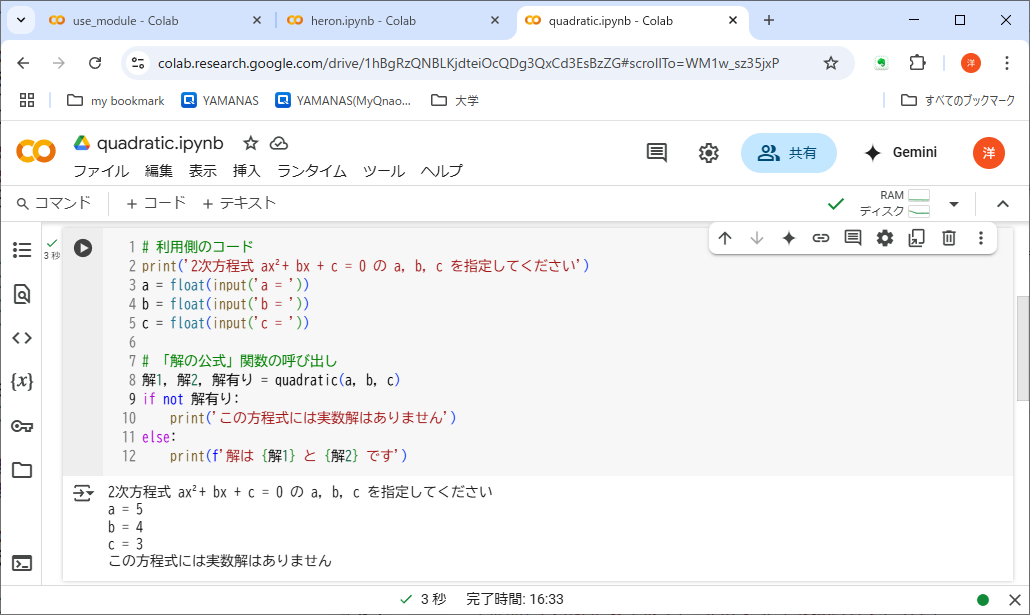
リスト9-3はない場合だ。

リスト9-3: 実数解がない場合

【参考】モジュールの定義と利用

heron()やquadratic()という新たなユーザ関数を定義できたが、その詳細（計算内容）はノートブック内のコードセルに残ったままだ。「詳細の隠蔽なんてできてないじゃん」というのはもっともな疑問だ。
関数を別ファイル（heron.py）で定義し、利用側でそれを「import heron」できれば、詳細は完全に隠蔽できる。つまり関数だけでなく、関数を含むファイルを新たな「モジュール」として定義するわけだ。
実は私たちは、これまでの回でも以下のようにモジュールを利用している。 


import sys
import math
from math import sqrt
最初の2つはsysやmathモジュール全体を利用する宣言、最後のは、mathモジュールの中のsqrt( )関数だけを利用する宣言である。ただし、これらはあらかじめ用意されたシステムモジュールだから、私たちは内容を気にせず、使い方さえ知っていればよかった。heronモジュールでもこれらと同じことができないか？
残念ながら、Colabのノートブックから自前のモジュールを利用する手順はやや込み入っており、しかもPC上のプログラムと異なる特殊なやり方を含んでいる。この節を【参考（＝授業範囲外）】としたのはそのためだ。
例として、上で定義したheron()関数をファイル「heron.py」として独立させ、別のプログラム「use_module.ipynb」からimportして利用する手順を説明する。
  1. つぎのプログラムをコピペして「heron.py」ファイルを作り（これがモジュールとなる）、利用側と同じディレクトリ（/content/drive/MyDrive/Colab Notebooks）に置く。 
    
# 「ヘロンの公式」関数
from math import sqrt
# 「ヘロンの公式」関数の定義
def heron(a, b, c):
    s = (a + b + c) / 2
    T = s * (s - a) * (s - b) * (s - c)
    if T < 0:
        return -1    # 定義域(?)のエラー
    return sqrt(T)
  2. 利用側のプログラムをリスト9-4に示す。まず最初に、外部（Googleドライブ）ファイルを利用するときと同じ「オマジナイ」をコードセルとして実行する。モジュールも外部ファイルなので、この準備段階が必要だ。
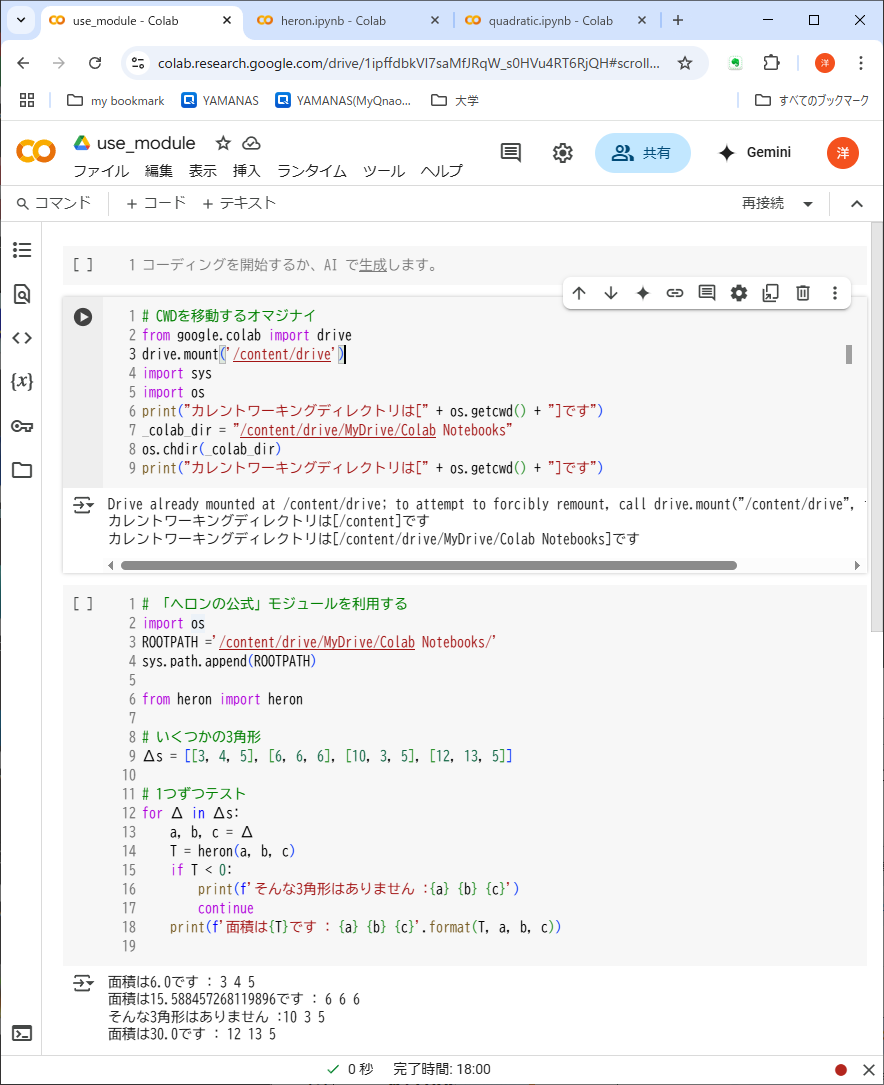
    リスト9-4: heronモジュールを利用するプログラム(use_module.ipynb)
  3. 「from heron import heron」という文で、「ヘロンの公式」モジュールの中のheron()関数だけがインポートされる。この場合、インポートされるのは「heron」という名前だけなので、呼び出し側では「T = heron.heron(a, b, c)」ではなく「T = heron(a, b, c)」と書かなくてはならない。
  4. 実行すると、heronモジュールに隠蔽されたheron()関数が呼び出され、いくつかの3角形の面積が順次求められる。

この方法なら、heron()関数の詳細（＝ヘロンの公式の定義）は完全に隠蔽される。この例ではリスト（のリスト）に格納された複数の3角形の面積を求めるのに使っている。モジュール化することで汎用性が増したのである。
このようにモジュールは関数より1段階上位の構造化単位である。関数とモジュールを活用すれば、より大規模なプログラムに取り組むことができ、自分が一度作成したコード資産を再利用できる。
ここで、Δデルタという変数名を使ってみたのは、文字コードがutf-8だからこそできる「お遊び」である。すでに「解1」「解有り」といった変数を使ったからお気づきだろうが、PythonのプログラムはUnicode(utf-8)で書かれており、ASCIIとShift-JISが混在しているのではないから、変数名や関数名は日本語にできるし、Unicodeに搭載されている国語ならなんでもよい※5。

5　だからと言って、提出課題にチャガタイ・テュルク語の名前を使うのはやめてほしい。

さらに、モジュールを集めて別のディレクトリにまとめることもできるが、そのためには関数やモジュールより上位のパッケージという構造化単位を利用しなければならない。いろいろ試してみたが、Colabでは特別な工夫も要るようなので、授業では扱わない。興味ある人は教科書の「step24」を参照してほしい。