第5回データ構造（リスト）、繰り返し(for)

変数と関数、条件分岐や繰り返しなどの制御構文さえあればなんでもできるのかといえば、まだ足りないものがある。多くの値を格納するための「データ構造」と呼ばれるものだ。いままで使っていた変数も、一番単純なデータ構造だが、これだけでは多くのデータ（たとえばみなさんの身長とか）をつぎつぎに処理するプログラムは書けない。また、前回扱った「素数の判定」も、効率よくできない。
今回は、Pythonがもつ基本的なデータ構造のうちリストについて学ぶ。また、whileとは違う、もう1つの繰り返し構文forの使い方と、それがリスト内の要素（データ）を処理するのに便利であることを学ぶ。

リストとスカラー

リスト（変数）は、他の言語でいう配列に似たデータ構造で、1つの名前で複数の値を格納できる変数である。これに対し、これまで使ってきた普通の変数（1つだけの値を格納できる変数）を、スカラー（変数）と呼ぶ。
スカラーとリストの違いは、一軒家と集合住宅とか、1輌の車と列車をイメージするとよく分かる。後者のイメージで描いたのが、図5-1である。

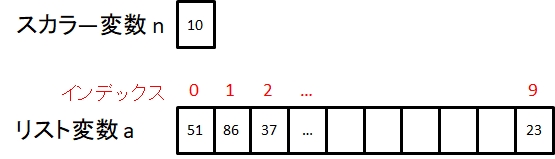
簡単のため、ここでは1輌に1人の乗客（つまり1つの値）が乗っているとする。スカラー変数nには、10という値が格納されている。一方、リスト変数aは、10輌編成になっており、10個の値が格納されている。
ただし、リストの場合、格納しただけでは、ある値が何番目に乗っているかわからないので、それを明示するための号車番号に当たるのが、インデックスという整数である。現実の列車と異なるのは、インデックスが0から始まることで、10個のリストであれば、インデックスは0～9である。インデックスは、リスト変数名の後に[　]をつけ、そこに入れる決まりである。つまり、図4-1の状態は、


# スカラー変数
n = 10

# リスト変数
a[0] = 51
a[1] = 86
a[2] = 37
　　：
a[9] = 23

と書けるが、リスト変数への代入はまとめて、


a = [51, 86, 37, … , 23]

と書くこともできる。

プログラム内でリストを作るのは簡単だ。要素を並べて[ ]で括るだけでよい。リスト5-1に例を示す。

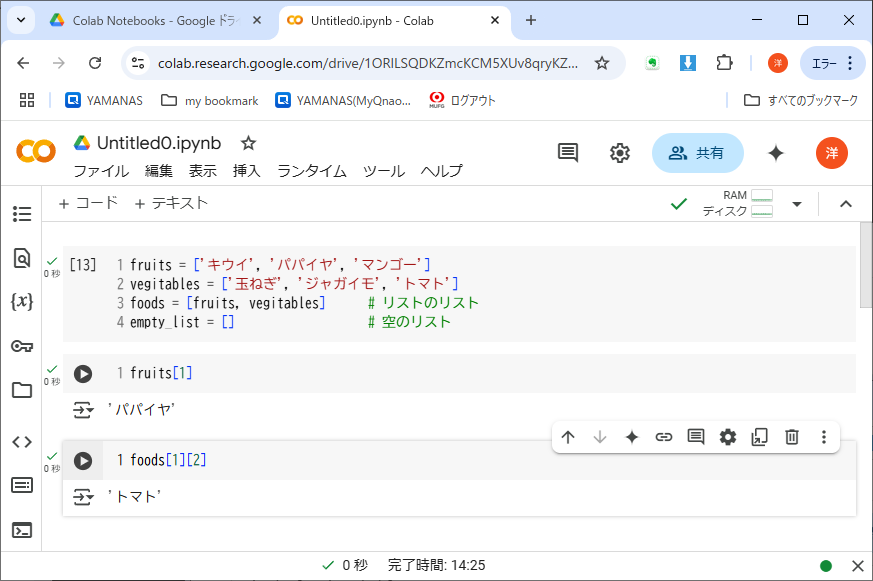
他の多くの言語のような、多次元リストはないが、リストの要素として別のリストを格納できるし、その内側要素に多次元リスト風にアクセスできるから、不便ではない。たとえばリスト5-1では、2つ目と3つ目のコードセルで、リストの要素にアクセスしている。

【参考】タプル

タプル（変数）は、リストとほぼ同じだが、中の要素は定義時に固定され、値を後から追加、削除、変更できない（これを「イミュータブル」という。反対にリストは「ミュータブル」だ）。
タプルでできることはすべてリストでもできるので、初心者のうちはリストだけを使う方がよい。処理速度やデータ容量が問題になったときに、値が変更されないと分かっているデータを、リストからタプルに変更すれば対応できるからだ。
タプルを作るには、要素を並べるだけでよいが、分かりやすくするために( )で括ることが認められている（つまり、リストが[　]を使うのに対しタプルでは(　)を使う、というわけではない。この点は初心者ばかりか、中級者もたまに勘違いしている）。リスト5-2に例を示す。

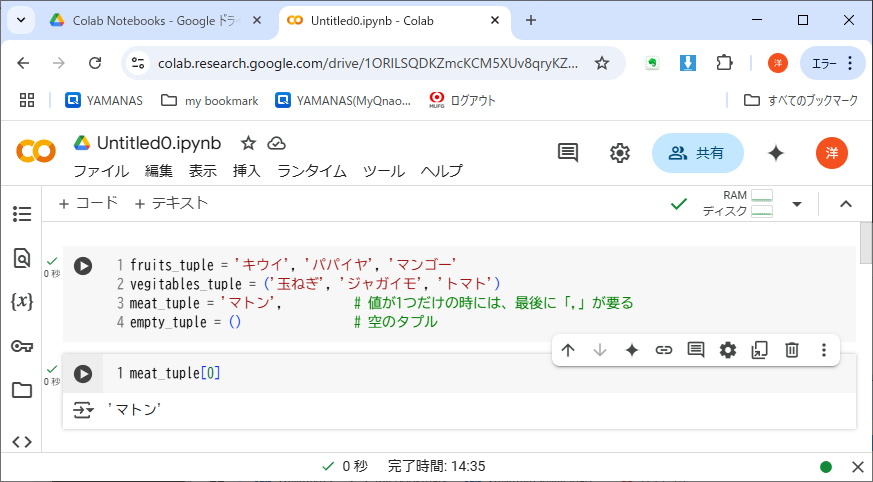
タプル回りの文法が微妙に混乱しているように感じるのは、私だけだろうか。
タプルのタプルや、タプルのリストも作れるが、初心者は混乱しそうだから、手を出さない方が無難だ。この授業のサンプルプログラムでは、リストだけを用いている。
ただし、タプルはむしろリストの代替よりも、関数への可変個の変数の引き渡しとか、関数からの複数値を受け取りなど、Python文法のあちこちで暗躍している。いわばPythonの「アンダーニンジャ」だ。

平均身長を求める

冒頭で代入された10人分の身長データ「tall」を元に、平均身長を計算する（リスト5-3）。

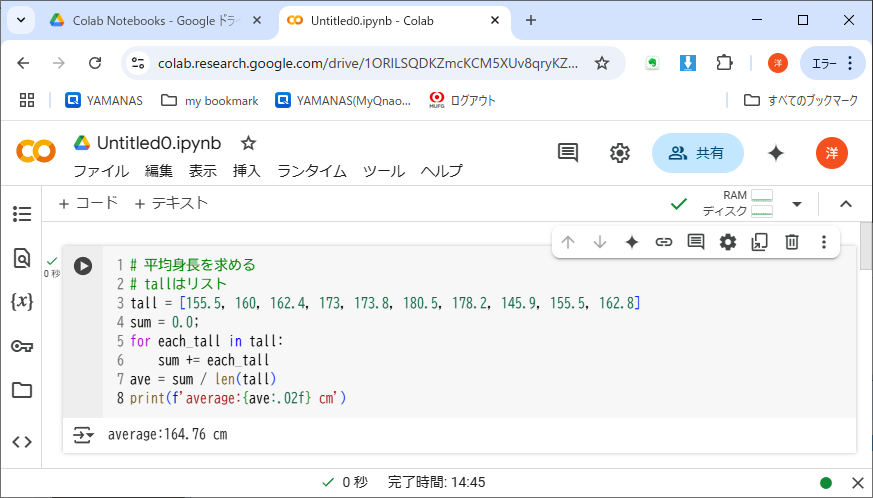
このfor文では、リストの要素それぞれが変数each_tallに代入されてループし、最後の要素を処理し終われば脱出する。リストとfor構文がうまくマッチした、わかりやすい表現である。len()関数はリストの長さ（要素数）を返す
最終行は、やや分かりにくいが、変数aveを「小数点下2桁の浮動小数点数として出力する」という書式制御構文（f文字列）である。「書式制御」と「f文字列」については、第10回の授業で正式に扱うが、Pythonの比較的新しい機能で、きわめて便利なので、ぜひ常用すべきだ^※2。

2　残念ながら教科書には解説がない。参考サイトを挙げておく。

for文

while構文はPythonにおける繰り返しの基本である。しかし、繰り返しには、ループ変数の初期化(i = 2)や、ループ毎の後処理(i += 1)といった処理がつきものである。これらをまとめて記述できれば、プログラムはもっと効率よく,わかりやすく書ける。
そこで使われるのがfor構文である。これを用いれば、前回の階乗を求めるプログラム（リスト4-5）は、リスト5-4のようにやや簡単になる。

ミソは5行目のrange(2, n + 1)で、これは2からnまで（n + 1ではない！）、1ずつインクリメント（加算される）される整数を変数iに代入しながら繰り返すという意味である（後の節「for文とリスト」で詳述する）。
新しい制御構造をマスターすると、プログラムは簡略化されて短くなり、その分バグを作り込むリスクも減る。

素数をリストアップ

ようやく前回の「素数の判定」のプログラムを超改良する機会がきた！あの時、効率がたいへん悪いと知りながら何もできなかったのは、スカラー変数しか使えなかったからだ。多くの数について「素数かどうか」「調べるべきか」をチェックし記憶する手段がなければ、シラミ潰しに調べる以外に方法はない。しかしリストを使えば、大幅に効率はよくなる。
せっかくリストを使うのだから、1つの整数を判定するだけでなく、2から120までの整数から素数をリストアップするプログラムに挑もう。それぞれの整数に「印」をつけられるデータ構造（リスト）を使えば、素数の倍数を「非素数」にマークし、後のテストから除外できる。
このアルゴリズムはエラトステネスのふるい(Eratosthenes' Sieve)といい、紀元前3世紀のギリシャの哲学者の発明とされる。この原理を示すすばらしいGIFアニメーションを見つけたので、図5-2で紹介する。しばらく眺めているだけで、アルゴリズムがたちまち理解できる^※3。

3　このような動く図の説明力は、教材作成などにもっと活かされてよい。説明のための最強のメディアといっても過言ではない。

2から120までの整数を記した碁盤目のようなものがふるいである。すべての整数はまず、無条件に「素数」としてマークされている（定義上、1は素数ではないので除外されている）。つぎに、素数である2がリストアップされるが、その際、すべての2の倍数は「非素数」とマークされ、以後のテストから除外される。同様の手順を3、5、7……について繰り返せば、多くの整数が「非素数」として「ふるい落とされる」ので、最後に残った整数が素数である。
いままで、このアルゴリズムを実現できなかったのは、この「ふるい」に相当するデータ構造が作れなかったからだ。そこで、リストprimeを使って「ふるい」を作り、プログラミングしたのがリスト5-5である。


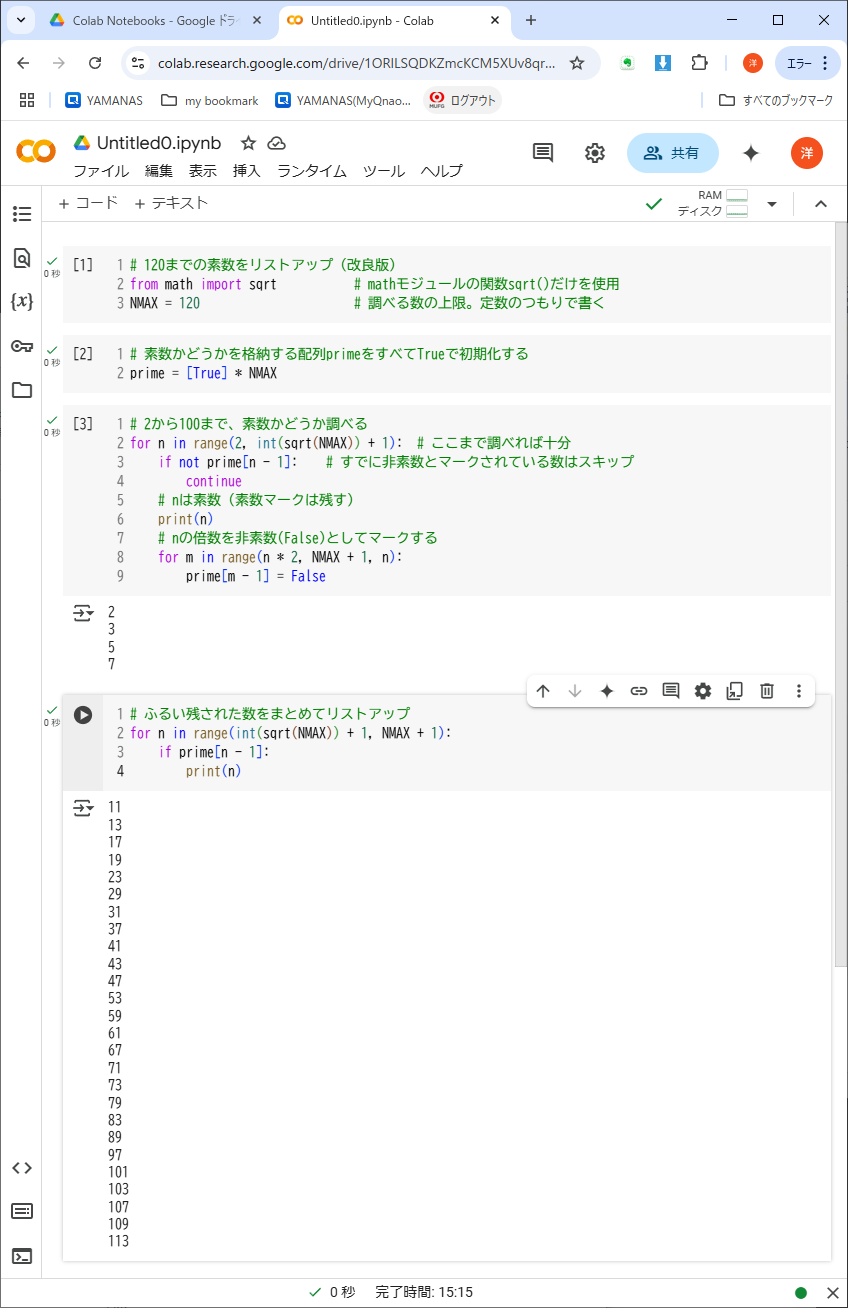
from math import sqrt

は、math（数学関数）モジュールから平方根関数sqrt()だけを参照する書き方である。この場合、プログラム中では「math.sqrt()」ではなく「sqrt()」と呼ぶ。このようにPythonでは、モジュールから関数という「部品」を個別にインポートできる（より正確にいえば、importされるのは関数ではなくsqrtという名前である）。
最初に120要素からなるリストprimeを、すべて定数Trueで初期化している。ここではリストの代入が起こっている。リストと整数の乗算がどのような意味で定義されているかを理解しよう。
prime[1]～prime[119]までしか使っていないのは、先に述べたように、1は定義上素数ではないからだ。また、「素数・非素数」とマークされている整数は、インデックスより1だけ大きいことにも注意。たとえばprime[96] == Trueは、整数97が素数であることを表す。
このプログラムは2つの（「2重の」ではない）for構文からなっている。最初のforで、2から7までを無条件に素数としてリストアップするが、同時にその倍数はすべて非素数(False)としてマークしている。11以上はテストせず、2つめのforで、ふるい残された数をそのままリストアップしている。なぜ11以上はテストしなくていいのか考えよう。

for文とリスト

while文もfor文も同じ繰り返し構文なら、なぜ前回まとめて説明しなかったのかと不思議に思うかもしれない。それは、他言語に比べてPythonのfor文が特殊で、より機能豊富だからだ。具体的にいえば、Pythonのfor文はリストと強く結びついており、本来はリストを学んだ後で解説すべきものである。
他のメジャーな言語（C系やjava）にもfor文は備わっている。ちょっと脱線になるけれど、ここでC系言語でのfor構文について見てみよう（ちょっとした比較言語学）。リスト5-4の4～6行目は、C++ならばこう書く。


// C++のコード（Pythonではない）
power = 1;
for (int i = 2; i < n + 1; i++) {
    power *= i;
}

forに続く()内は、「;」記号で3つの部分に分かれている。

最初の部分は、ループ変数iの初期化
2番目の部分は、ループの継続条件
最後の部分は、ループ毎の末尾で行う処理（「後始末」）

つまりこのfor文は、あくまでwhile文の進化版にすぎない。
一方、Pythonのfor文はどうか。リスト5-4の該当部分をもう一度見てみよう。


power = 1
for i in range(2, n + 1):
    power *= i

上の節「for文」では、range()関数について、「リスト」という言葉を使わない適当な説明をしたが、実際はこういう意味である。
renge()関数は、これは2から始まってnまで（n + 1ではない！）、1ずつインクリメント（加算）される数値の「ストリーム」を返す^※4。ストリームは、さきほど解説したリストと混同しても、今はまあ問題ない。
つまり、for文は


for 変数 in リスト:
    ループ本体

という構造を持っている。リストだけでなく、なんらかの繰り返しができる列に類するものならなんでもよく、文字列だってよいし、後の回で学ぶが、1つのファイルの全行だってよい。変数には列中の値が1つずつ、全部処理されるまで順に代入され、最後の要素が処理されるまで繰り返される。
Pythonのfor文が特殊で機能豊富という意味がお分かりになっただろうか。

4　厳密にいえば、range(start, end, step)は、整数startから始まり、step刻みで、end - 1までの整数を順に生成するジェネレータである（上の例では、第3引数stepは省略されてデフォルトの1と見なされている）。ちょっと難しいが、あらかじめリストを生成するのではなく、次々に生成(generate)した値をiに渡してゆく仕組みである。

第5回 データ構造（リスト）、繰り返し(for)