第4回 実行の流れの制御:条件分岐(if)、繰り返し(while)
前回のサンプルプログラムでは、実行の流れは上から下への一直線であり、自然とできることも限られていた。条件分岐(ブランチ)と繰り返し(ループ)という「実行の流れを制御する構文」を学べば、できる処理がはるかに広がる。
今回は、いくつかの数値計算を課題に、Pythonプログラムでの実現法を考えてみよう。
この回の内容
奇数か偶数か調べる
冒頭で変数nに代入された整数が奇数か偶数かを判定するだけのプログラムだが、2通りの場合分けがあり、それぞれで動作(表示されるメッセージ)が異なる。サンプルプログラムをリスト4-1に示す。amariを計算するために剰余演算子「%」が使われているのに注意(教科書9ページを参照)。これは前回登場した割り算の「商」を表す演算子「//」とペアをなす。
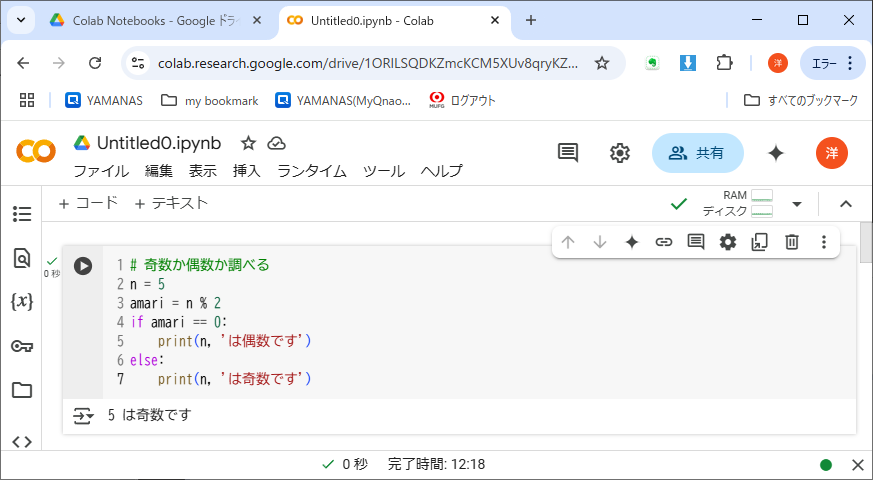
調べる整数、つまり対象データは、2行目で代入された変数nである。2で割って奇数か偶数かテストされ、amariが0(つまり偶数)ならif文以下の「コードブロック(実行文の集合)」が実行される。amariが1(つまり奇数)ならelse文以下のブロックが実行される。どちらも実行されなかったり、両方が実行されることはない。これを排他的処理という。学校数学では「場合分け」と呼んでいた。
なので、このプログラムをテストするには、少なくともnに偶数、奇数の両方を代入して2回以上実行しなければならない。このようなテストデータの集合をテストセットと呼ぶ※1。
1 こんな単純なプログラムならともかく、複雑で大規模なシステムで、完全なテストセットを設計するのはたいへん難しい。まれな条件が重なって、今まで1度も実行されていなかったコードが実行され、長年そこに潜んでいたバグが大トラブルに発展したこともある。前世紀末に起きた「2000年問題」もその一種。
「if 《条件式》:」や「else:」の行末の「:(コロン)」を忘れないように。Pythonではあらゆる制御構文の行末にこの「:」がつく。これは、条件式が成立したときと、非成立の場合に実行されるコードブロックの始まりを意味する。それぞれ、- ifブロック
- elseブロック
ほとんどの言語(C系言語やjava、PHPなど)では、コードブロックは中括弧{ }で明示されるが、Python言語の流儀は風変わりで、この「:」と、その次行から始まる行頭のインデント(字下げ)が実行ブロックの範囲を明示する。つまり、他の言語のようなプログラムを見やすくするインデントではなく、文法的な意味を伴うインデントなのである※2。
2 テキストエディタでプログラムを書く場合など、多数行にわたってインデントを揃えるのは、正直やや面倒くさい。この変わった言語仕様は、「どのプログラマが書いてもコードが大体おなじ姿になる」ように決められたそうだが、果たしてどの程度効果があるのだろう。ここだけの話、「一生涯使い続けます」と神に誓えば、秀丸エディタで4カラム分に設定したタブを使ってもいいと、個人的には思っている(初心者のみなさんには奨めないが)。Pythonの生みの親Guido van Rossumのバイブルに、「インデントは半角空白4つとし、タブを使ってはならん」と厳かに書かれてしまっているので、きっと私のは異端の神なのだろう。さいわい、ColabやVisual Studio Codeなどの開発環境は、自動的にインデントされるので、この問題でさほど悩まないで済む。
うるう年の判定
場合分けの数は2つとは限らない。うるう年を判定するロジックは、西暦年を4通りに場合分けする。だから最終的には4分岐が必要だが、if構文によるpythonの分岐は、条件式(真(True)か偽(False)のどちらかの値をとる論理式)が判断基準なので、1度には2分岐しかできない。
したがって4分岐を実現するには、「if~else」構文を3つ、段階的に※3使うしかない。サンプルプログラムをリスト4-2に示す。
3 これを「カスケード(cascade)状」という。階段状に流れる滝の意味で、西洋風庭園でよく見かけるアレだ。
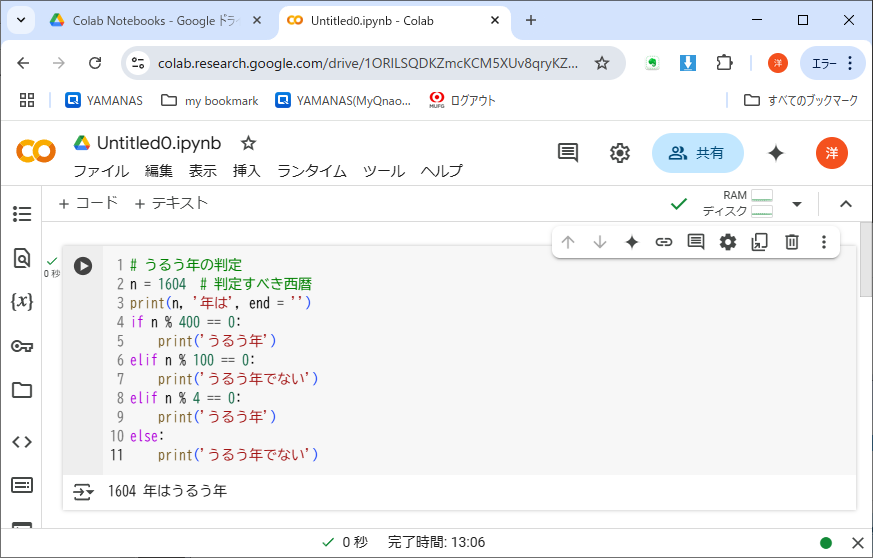
しかし、そうしたカスケード状の分岐をifとelseだけで書くと、インデントがどんどん深くなってしまう。そこで「elif 《条件式》:」が使われる。これは、
else:
if 《条件式》:
うるう年のような多段階の判定では条件の厳しい方から、つまり「西暦が400で割り切れる」最もレアなケースから先に判定する。他人に「うるう年のルール」を説明してみるとわかるが、これは人間の自然な思考と逆なので、多少慣れが要る。しかし、そうしないと、つぎつぎに発生する例外の処理に追われてしまう。
論理演算子(andとor)
多段階分岐とは別のやり方もある。if文は条件式の真偽によって2通りにしか分岐できないが、条件式自体を複雑にすれば、同じロジックを2分岐で書ける。
多くのプログラミング言語と同様、Pythonには論理演算子が用意されている。単純な論理式をつないで複雑にする2項演算子である。
リスト4-3は、リスト4-2の判定プログラムを、論理演算子を使って2分岐に書き換えたものだ。
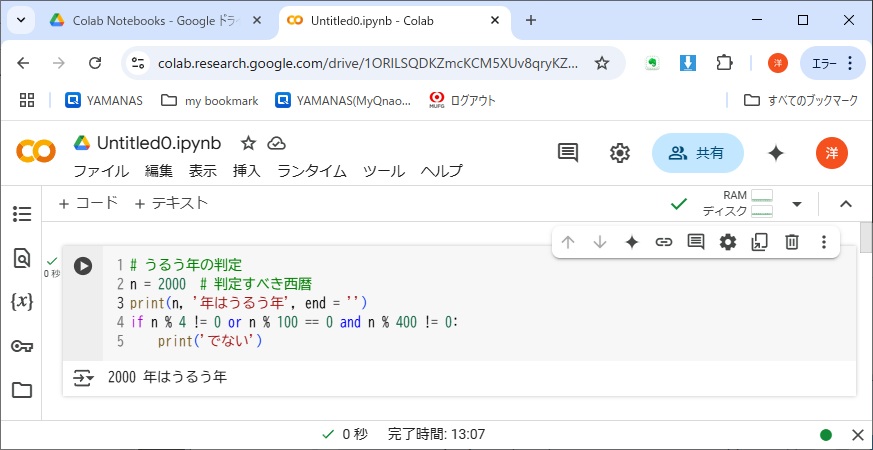
andはかつ、orはまたはを意味する。したがってこの条件式は、「西暦が4で割り切れないか、または、100で割り切れてかつ400で割り切れない(とき、うるう年でない)」ことを意味している。
このように、andとorを併用する場合は、andはorより先に計算される。小学校で習う×は+より先に計算するという規則と同じだ。優先順位の低いorをandより先に計算したい場合に( )で囲むのも、四則演算と同じである※4。
4 andを論理積、orを論理和と呼ぶのはそのためだろうか。
条件式を簡単にして多くのif文を書くか、それとも条件式を複雑にしてif文を1つにまとめるかは、トレードオフ関係である。一概にどちらとも言えないが、あまり複雑な条件式はプログラムの可読性を著しく損なうので、何事もやり過ぎは禁物だ。
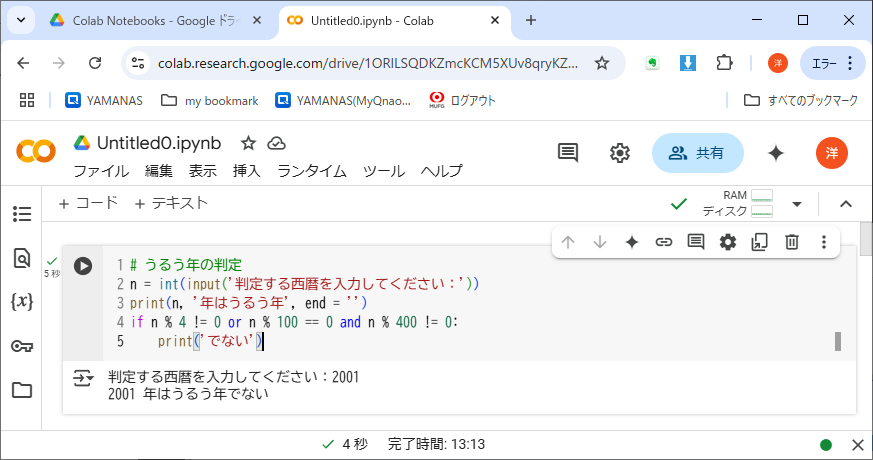
今回のサンプルプログラムでも、判定すべき西暦という対象データはプログラムに直接書きこまれていて、異なる西暦をテストするには、いちいちプログラムを書き換えるしかない。まったく実用的ではない。前回学んだinput()関数で、西暦をユーザに入力させてもよいかもしれない(リスト4-4)。
実行の流れの制御:繰り返し(while)
階乗
この単元では、同じ(ような)処理を何度も行う繰り返し(ループ)構文について学ぶ。そもそもプログラムはたくさんのデータを一挙に処理するために作られるので、一直線のプログラムはあまり実用的ではない。そこで、たくさんのデータを「次から次へと処理する」ために、繰り返し構文が必要になる。つまり、プログラムの同じ部分が2回以上実行されることになる。
プログラムの処理は同じでも、扱われるデータはもちろん異なる。そうでなければ繰り返し計算する必要はない。ただし、イルミネーションの点滅とか、繰り返すこと自体に意味がある制御プログラムは例外。
ここでは、階乗(power)を計算する。ある整数の階乗とは、1からその整数までのすべての整数を掛け合わせた数のことだ。整数nの階乗をn!と表し、たとえば
5! = 5 * 4 * 3 * 2 * 1 = 120
問題:40-32÷2=?
小学生「4!」
理系「よくわかってんじゃん」
文系「やっぱわかんないか~w」
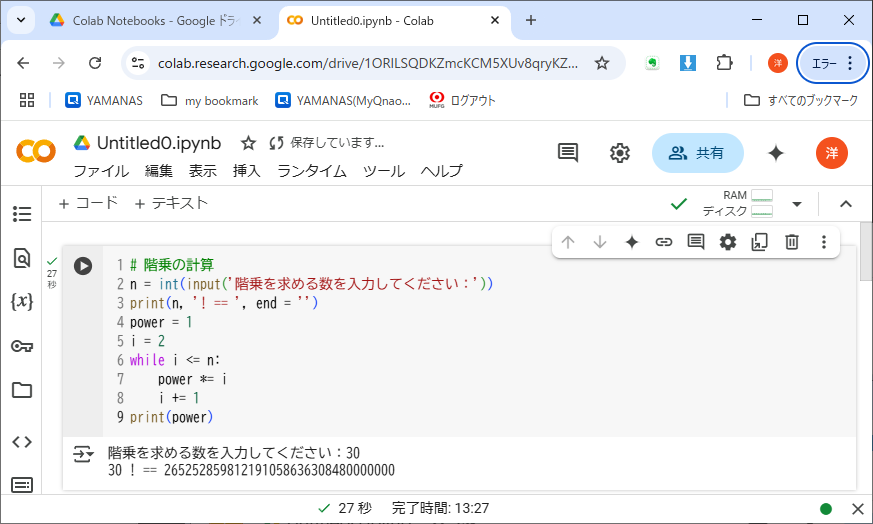
というギャグを見かけたが、これの元ネタが階乗である。リスト4-5にプログラムを示す。
while文
ここで使われている繰り返し構文は「while 《条件式》:」である。条件式が成り立つ間、つまり真(True)である間だけ、後続の「whileブロック(範囲はインデントで示される)」を繰り返し実行する。つまり、この条件式は終了条件ではなく、継続条件を表わしている。print()関数は、変数n、文字列定数('! == ')とオプション引数(end = '')が渡されている。オプション引数以外は順番に連結されて出力される。オプション引数の種類や意味は、関数毎に決められているので調べるしかない。この場合は行末の改行を抑止する。
このプログラムでは、階乗を求める数をnに入力してもらい、階乗を作る変数powerに初期値1、ループ変数iに初期値2を代入している。そして、iを1ずつ増やしながら、powerにiを「かけ込んで」ゆく。
whileループから抜け出すのは、iがnより大きくなり、while文の条件式が成立しなくなった時で、実行点は最終行(whileブロックのつぎの行)に飛び、階乗の計算結果を出力して終わる。
計算結果を見ると、Python処理系が4バイトや8バイトといった制限を超えた巨大な整数(30!)を扱えることがわかる(どのように実現されているのかは、私たちユーザは知る必要がない。
素数の判定
条件分岐と繰り返しを組み合わせれば、どのように複雑なロジックでも表現できる。
ここでは、ある数が素数かどうか調べるプログラムを考えよう。冒頭でユーザが入力した値を代入された変数nが、調べる対象データである。
素数とは1とその数自身しか約数を持たない整数だから、2から始めてしだいに大きな数で割ってみれば(いつかは)判定できる。途中で割り切れれば素数ではないし、最後まで割り切れなければ素数だ。このナイーヴな発想を形にしたのがリスト4-6である。
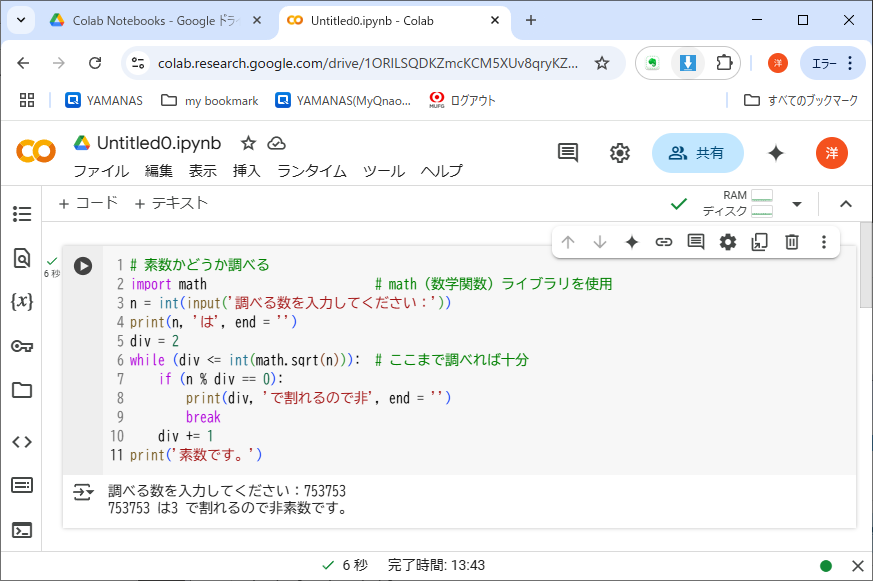
import mathは、数学関数モジュールを使う宣言である。そこに含まれる平方根関数sqrt()を使いたいからだ※5。
5 Pythonのモジュールは他の言語のライブラリに相当するもので、Pythonコードをまとめたファイルだ。このように、Python処理系自体にはない機能も、各種モジュールをimportするだけで使える。どんなライブラリがあるかは、Webなどで検索すれば分かる。Pythonのコミュニティはとても大きい(数千万人~1億人以上)ので、われわれ凡人が思いつくようなことには、たいてい便利なモジュールが見つかる。Colabですぐにimportできるものもあるし、実行して「見つからない」といわれる時には、コードセルで以下のコマンドを実行すれば使えるようになる。
!pip install 《モジュール名》
例) !pip install openpyxl
除数divはなぜ「ここまで調べれば十分」なのか、考えよう。
while文の内側にif文がネストされて、インデントが2段階になっているのに注意しよう。それぞれの行は何らかのネストレベルに属している。たとえば「div = 2」はネストレベル0、「break」はネストレベル2というように。このbreakは初出だが、whileやforループからただちに抜け出すことを示す※6。
ところでこのアルゴリズム(計算手順)は、ナイーヴなだけあって、効率的とはいえない。たとえば、2で割れなかった数を4で割ってみるのは無駄だ。もう少し効率アップできないか? それには次回登場するリスト(変数)を学ぶ必要がある。
6 最近あまり見かけないが、以前は巨大迷路という施設があちこちにあって、一度入ると、抜け出すには小一時間かかる。ただ、気分が悪くなったり、子どもがオシッコに行きたくなった場合は、手を挙げてギブアップすると、どこからともなく係のお姉さんが現れて、根性無しの出口から外に出してくれた。breakはいわば、プログラム版「根性無しの出口」だ。ただし、脱出できるのは、最も内側のループだけである。