第1回 イントロダクション：この授業について

「プログラミング入門」は、1学期の授業で、履修者のみなさんが初歩のプログラミングを学ぶ科目である。言語としては、世界で最も普及しており、初心者にもやさしいとされるPythonを採用する。
「プログラミングとはなにか」「何の役に立つのか」なんて抽象的な話はパスして、早速本題に入りたいけれど、今回は初回なので履修者が確定していない（来週初参加の履修者もいるはず）。だから今回は、プログラミングのための基礎知識として、ICT（つまりPCやインターネット）で数値や文字の情報がどのように表現されているか※1について学ぶ。

1　みなさんの世代は、すでに小中高で基本を学んでいるはずですから、復習のつもりで聞いてほしい。

この回の内容

ICTにおける数値の表現

学校数学の「数」とICTの「数」

コンピュータやインターネットは「デジタル機器」と呼ばれるが、みなさんは「デジタル(digital)」という意味を説明できるだろうか。ちなみに語源は「数の」である。
これは、ICTではすべての種類の情報が最終的に「数（2進数）」に変換されることを指す。
もともとコンピュータ（計算機）は、人手だと膨大な手間がかかる計算を高速に実行する機械として誕生した。科学技術や経済・金融分野での数値計算である。
一方、ビジネスにおけるICT利用ではテキスト（文字）の処理が主であり、美術・音楽などの芸術分野や、地学・天文学などの科学分野では、画像（静止画・動画）や音声を処理するニーズもある。コンピュータの進歩につれ、最初は数値だけだった処理対象の「（表現）メディア」が文字・画像・音声へと広がったわけだ。
だが、もっとも基底の、コンピュータのCPU（中央処理装置）が処理しているレベルでは、依然として「数値計算」しかしていない。つまり、コンピュータにとっては、文字や画像、音声の処理も、すべて「計算」なのだ。
だからICTでは、共通に利用できる数の表現が、日本工業規格(JIS)や国際標準規格(ISOやIEEE、ASCIIなど)で規定されている。
今回はそのうち、プログラミングに必要なものだけを学ぶ。

学校数学の「数」とICTの「数」

まず知っておいてほしいのは、みなさんが学校数学で習った「数」と、ICT環境で規定された「数」はかなり違うこと。その対応を図1-1に示す。

図1-1: 学校数学の「数」とICTの「数」

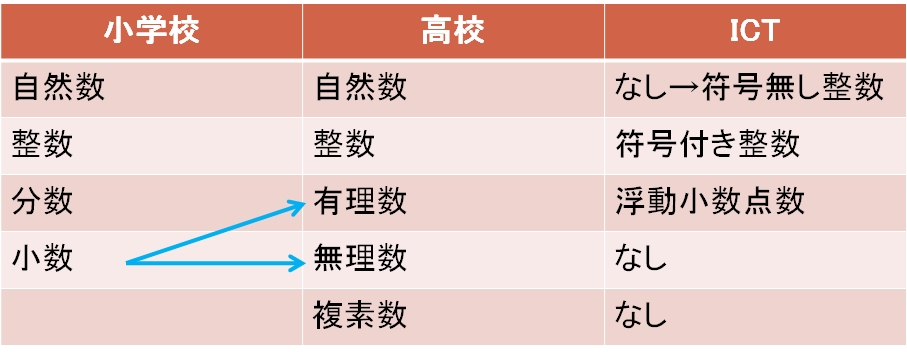
学校で習う数には自然数、整数、分数、小数、複素数など、さまざまな種類があるが、ICT環境ではこれらを

に3分類する。数学の「数」よりも種類が少ないから簡単だ（Pythonにはcomplex型＝複素数もあるが、この授業では使わない）。その代わり、ICTでは上記それぞれの数を格納する記憶容量（メモリサイズ）も区別しなくてはならない。それも含めると、ICTの数値は、以下のように分類される。
True/False
Pythonではbool型（Boolean型）と呼ばれる（2進数の1桁＝0か1に相当）
整数
1, 2, 4 … BYTE（表現できる数の範囲が異なる）
  • 符号なし整数
  • 符号つき整数
浮動小数点数
2, 4, 8 … BYTE（表現できる数の範囲と精度が異なる）
  • 半精度浮動小数点数(FP16) 2 BYTE
  • 単精度浮動小数点数(FP32) 4 BYTE
  • 倍精度浮動小数点数(FP64) 8 BYTE

2進数(binary number)

コンピュータでは、数値も、文字・画像・音声なども、最終的にはすべて「2進数」で表現される。私たちが普段使っているのは、0から9までの10種類の数字を用いる「10進数」だ。つまり2進数は、0と1の2種類の数字だけを用いる表記法である。
なぜICTではこれを使うのかといえば、

など、2通りの状態をもつ物理現象なら、なんでも2進数の1桁(bit)を表現できて便利だからだ。
10進数表記と区別するため、数学の教科書では2進数の表記には、「10012」のように添え字がついていた（覚えているだろうか）。でも、この講義資料を含め、ICTの解説ではたいがい省略される※2。

2　じゃあどうやって区別するのかといえば、前後の文脈で区別する。つまり「空気を読め」ということ。

例として、10進数と2進数の対応を示すと、 である。

3　「ヒャクイチ」と読んでいいのは10進数だけで、これは「イチレイイチ」または「イチゼロイチ」と読む。

16進数と8進数、基数変換

デジタル情報の最小単位はビット(bit)である。これは「情報工学の父」クロード・シャノンが名付けた、「2進数の1桁(binary digit)」を表す造語。数学的には確率1/2と結びつけて定義されている。別のいいかたをすれば「2種類のモノを区別できる情報量」だ。
このように2進数は、ICT内の物理現象と1対1に対応するが、さきほど述べたように、10進数の100や50000といった比較的小さな数さえ多くの桁数を必要とするので、ICTのテキストを書いたり設計するには「表記法」自体が不便だ。つまり最小単位なのはいいが、単位として小さすぎる。そこで、コンピュータの内部では、「1bit」より、2進数を8桁まとめた「1BYTE（1バイト）」が、あたかも最小単位のように使われる。「256種類のモノを区別できる情報量」である。
表記法も、2進数の4桁を1桁にまとめた16進数(hexadecimal number)などが使われることが多い。ICTではこれも2進数と同様、基数の16を右下の添え字ではなく、数字の頭に0xの2文字をつけて、0x8e52のように表記する。これは16進数で4桁なので2進数の16桁、つまり2BYTEの情報を表している。
16進数では16種類の数字が必要なので、10進数で用いる0～9だけでは足りない。そこで、9の後にA～F（a～f）の6種類の数字があるものとして表記する※4。つまり、

となる。この等式は数の表記を変えるだけで、数学的には恒等式にすぎない。この操作を基数変換という。

4　仕事柄、AからFまでの6人を文字の世界から数値の世界に拉致ってきて、しかも「今日からお前たちは数字だ」などと洗脳している妄想が浮かぶ。

だから、16進数数に現れるA～Fは文字ではない。また16進数は、あくまで2進数を短く表記する便宜上の工夫に過ぎず、ICT内部ではあくまでもすべての数値（とデータ）を2進数で表現している。

演習：基数変換

10進数⇔2⇔16進数の基数変換をしてみよう。この作業には、図1-2に示す対応表を用いる。この表は、最も数字の種類が多い16進数の1桁が、他の進法で何に相当するかを示している（8進数については、この授業では扱わない）。

図1-2: 各基数の対応表

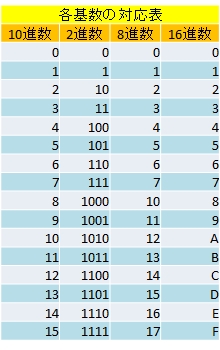
それと、1BYTE（2進数の8桁をまとめた単位）の数値を書き込める、図1-3のような「置数枠」をノートに描いておくと便利である。これは後述する1BYTEの符号なし整数に相当し、8つの枠に0または1が入る。枠下の数字は、各桁の「位」を表す。つまり10進数なら「1の位、10の位、100の位……」となるのが、2進数では「1の位、2の位、4の位……」となるわけだ。
またMSB（1BYTEの場合は128の位）は最上位ビット(Most Significant Bit)、LSB（1の位）は最下位ビット(Least Significant Bit)を表す。今後たびたび使うので覚えよう。

図1-3: 1BYTEの構造を表す「置数枠」

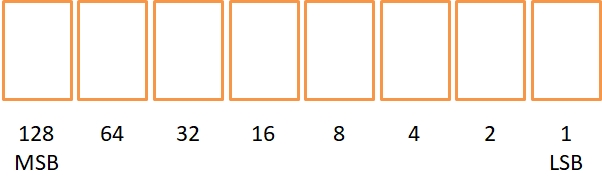
10進数→2→16進数の基数変換

【授業フォルダにワークシート「数値情報演習.txt」がある】
つぎの10進数を1BYTEの2進数および16進数で表現しなさい。

  1. 56
  2. 23
  3. 34

2, 16進数→2→10進数への基数変換

つぎの1BYTEの2進数および16進数を10進数で表現しなさい。
  1. 00100111
  2. 11110001
  3. 0x3F
Windowsの電卓をプログラマモードで使うと、2，8，10，16進数間の基数変換や四則演算が簡単にできる。
このように、ICTでは8bitの情報をまとめて1BYTEと呼ぶ。たとえば後で学ぶ文字コード（ASCII、Shift-JIS、Unicode：UTF-8の場合）は、それぞれ1文字につき1BYTE・2BYTE・3BYTEの情報であり、2桁・4桁・6桁の16進数で表現される。
その他、主に英語圏では、 などの単位もよく使われる（「電卓」のプログラマモードにも表示がある）。

符号なし整数の表現

ようやく整数の表現を説明する準備が整った※5。前述のように、ICTには自然数という概念はなく、代わりに自然数に0を加えた符号なし整数が用いられる。

5　「さっきまでのはなんだったの？」と思うだろうが、ここまでは2進数と基数変換の説明だった。

数学の「整数」には、値の上限や下限はないが、有限のメモリ上に数を格納するICTでは、必ず上限と下限がある。後述する浮動小数点数では、それに加えて精度の制限もある。
「符号なし整数」は、あるサイズの記憶領域に、前述の2進数をそのまま格納したものである。一般に、1, 2, 4BYTEの整数型が区別される。1bitの数値を格納する「bool型（yes/no型・Boolean型）」も、符号なし整数の1種と考えられる。
1BYTEの符号なし整数では256種類のモノ（たとえば0～255までの整数）を表現できる。図1-3に示した置数枠に、全桁0か1を入れてみれば明らかだろう。プログラミングの分野では、「符号なし整数」という数の種類と、格納するBYTE数をセットにしてデータ型(data type)と呼ぶ。

演習

2BYTEや4BYTEの符号なし整数では、どんな範囲の値が表現できるか？ Windowsの電卓（プログラマモード）で確かめよう。

符号つき整数の表現

日常生活と同様ICTでも、人数や体重の増減、赤字など、負の数を表現する必要はひんぱんに発生する。。紙の上ではマイナス（－）符号をつけるだけだが、ICTでは0と1だけで負数も表現しなければならないので工夫が要る※6。

6　負の数の表現は、正の数の表現に符号を表す1bitを追加したものではない。が、大抵のヒトがしている誤解を今日で終わりにしよう。

その工夫が補数である。1の補数と2の補数があり、ICTでは2の補数で負数を表現する。
1の補数
正数の各ビットを反転(negate)したもの（プログラマ電卓では、「Not」キーにこの反転操作が割り当てられている）。
2の補数
1の補数に1を加えたもの。また、正数のビット数nより1桁多く、最上位ビットが1、残りがすべて0であるような数値(n = 8なら 9桁の数100000000)から、正数を引いた数。計算結果の最上位桁（n + 1ビット目）は無視する。

演習

  1. 35の符号なし整数表現を求めよ。格納されるビット数nは16とする（1WORDの整数）。
  2. 1の補数を求めよ。
  3. 2の補数を求めよ。これが-35を表している。
  4. 35と、3で求めた-35を足し、0になることを確認せよ。最上位桁（MSB：17ビット目）は無視してよい。

2の補数を用いて正負の整数を表現すると、

となるので、結果的に最上位ビットを符号ビットとして扱える。
なぜこのような補数表現を用いるのだろうか。「A+B」という加算において、AとBの符号には4通りの組み合わせがある。したがって、もし負数表現として「符号ビット＋符号なし整数」を使うと4通りの場合分けが必要となり、何倍もの計算時間を費やしてしまう。「2の補数」なら場合分けは不要であり、はるかに高速に計算できる。加算と減算の区別も要らない。
ただし、同じバイト数の符号なし整数に比べて、符号つき整数では表せる正数の範囲が約半分になる（当然、その分は負数に割り当てられる）。たとえば1バイトの符号つき整数は、-128～127の値を表現できる※7。

7　なぜ負数の方が1種類だけ多いのか、考えてみよう。

演習

2バイトや4バイトの符号つき整数では、どんな範囲の値が表現できるか？ Windowsの「電卓（プログラマモード）」で確かめよう。

浮動小数点数

ICTにおける小数の表現である浮動小数点数(floating point nunber)は、かなり複雑だが、演習を通じてイメージを持つだけでも十分だ。
浮動小数点数とは、前述の符号つき整数を拡張し、数値を3つの部分に分けて表現したものである。

精度や有効数字に関する厳密な扱いを要する科学技術分野では、以前からこのような表現方法が使われてきた。科学的表記法(Scientific Notation)というもので、高校の理科の教科書で見覚えがあるだろう。たとえば、 などというアレだ。もちろんこれらは10進数表記である、

演習

光の速度とアヴォガドロ定数について、それぞれ符号、仮数部、指数部を答えよ。また、（10進数での）有効数字は何桁か。


浮動小数点数の表現は国際標準規格IEEE754で定義されており、ICTの各分野、たとえばプログラミング言語やデータベース、CPUの命令セットなどがこの規格に準拠している。この規格には、

などの種類がある※8。

8　4倍精度浮動小数点数もあるが、説明は省略。半精度浮動小数点数(FP16)は2008年版で新たに加えられたもので、背景には、GPUによるグラフィックス処理や機械学習などの分野で、精度よりも処理性能が重視されることがある。最近では生成AIの発展に伴い、BF16(brain floating point)などという新種も現れた。人間の脳は複雑だけど、個々の脳神経の精度はそんなに高くないということか。

図1-4に、単精度浮動小数点数の構造を示す。これだけでも印刷しておくと、演習のワークシートとして使えて便利だ。

図1-4：単精度浮動小数点数の構造

各部の定義を示す。

符号ビット
符号つき整数と同様に0:+、1:-
仮数部
2を基数として整数部が1桁（つまり1）になるように値をシフトし、1を引いて正規化した数の 2進数表現（ケチ表現）
指数部
真の指数に半精度の場合は15、単精度の場合は127、倍精度の場合は1023を加えた値。指数部としての範囲は1～30、1～254、1～2046に制限される。つまり、真の指数の範囲は、-14～+15、-126～+127、-1022～+1023である
つまり全体としてつぎの値を表現している（±は符号部で決まる）。
半精度
±(1+仮数部)×2指数部-15
単精度
±(1+仮数部)×2指数部-127
倍精度
±(1+仮数部)×2指数部-1023
ただし指数部はさらに複雑で、以下のような役割も持つ（単精度と仮定して説明する）。 かくも複雑な定義になったのは、限られたバイト数で表現範囲を少しでも広げ、誤差を少しでも減らす工夫を、世界中の学者がよってたかって盛り込んだせいである※9。

9　ここまで工夫を重ねたにもかかわらず、2進数の浮動小数点数と、私たちが普段使っている10進数の「小数」との相性はあまりよろしくない。なにしろ、10進数の0.1は、2進数で表すと、0.000110011001100110011...のように無限小数になるのだ。つまり、限られたわずかな種類を除いて、10進数の小数を2進数に変換すると誤差が生じるのである。たとえ「0.1」ですら！

演習

-18.25の単精度浮動小数点数表現を求めよ。図1-4をワークシートとして使うと便利だ。


ICTにおける文字の表現

ICTでは、最終的にすべての情報を2進数として扱うと述べた。したがって、さまざまな種類の情報を2進数に変換し、逆に元の情報に変換する対応規則（変換規則）が必要になる。「コード」「コーデック」「フォーマット」などと呼ばれているものがそれにあたる。音声や画像の対応規則は複雑なので、この授業では扱わない。

文字の表現

この単元では、プログラミングを学ぶために最低限必要な文字情報（テキスト）がICTでどのように表現されているかを学ぶ。文字情報と数値情報を相互変換する規則を文字コードという※10。

10　codeは元来重々しい言葉で、「規約」とか「掟」を指す。「目には目を、歯には歯を」のハムラビ法典はCode of Hammurabiだ。

テキストの最小単位は1文字である。ICTでは、すべての文字は文字コードによって数値に変換されて処理される。文字から変換された数値自体も文字コードと呼ばれ、大別してつぎの2種類がある。

1BYTEコード
アルファベット、数字、記号などを表現する文字コード。WindowsではASCII文字コードが用いられている。
多BYTEコード
日本語・中国語・韓国語・アラビア語など、256種類を超える文字をもつ言語は、1BYTEコードでは表せないので、2BYTE以上の文字コードが使われる。日本語の文字コードには、以下のような種類がある。
JISコード
JIS（日本工業規格）やISO（国際標準規格）で規定されている2BYTE文字コード
Shift-JISコード
　日本のパソコンで広く用いられている2BYTE文字コード。JISコードをASCIIコードと併用する際の不便を解決するために開発された。
EUCコード
Linux系のワークステーションなどで用いられている2BYTE文字コード。Shift-JISコードと同様の動機で開発された
Unicode
世界中のすべての文字を共通の文字集合で表現するために開発されたマルチBYTEの文字コード。Windowsパソコンの内部処理など、主要な用途に広く用いられている。Pythonでは、UnicodeのUTF-8という文字符号化スキームを用いる（日本語も英数字も）

ASCII文字コード

まず、英数字を表現するASCII文字コードについて学ぶ。図1-5にASCII文字コード表を示す。

図1-5: ASCII文字コード表（出典：IT用語辞典）

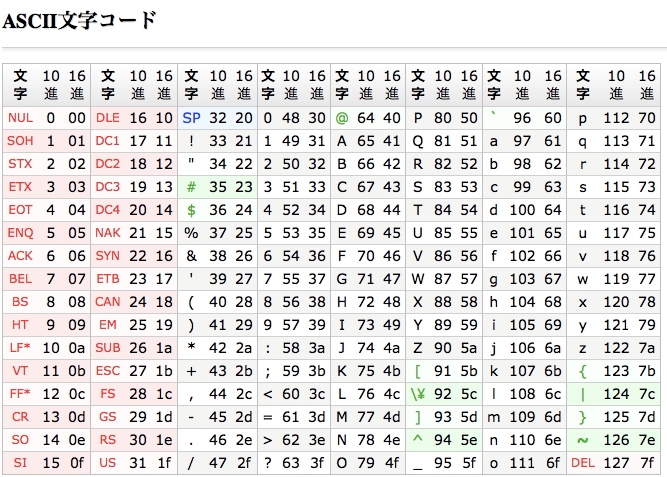
たとえばAは10進数の65（16進数では0x41）と対応する。この授業では以後、16進数表記を使う。しかしメモリ上の1BYTEに書かれた「0x41」が数と文字のどちらを表すかは、データ自体から判断できないので（画像や音声、あるいはプログラムの一部かもしれない）、それはプログラム側で区別しなくてはならない。
図1-5から分かるように、1BYTEコードと言っても、英数字や記号類には128種類で足りるので、ASCIIコードのMSB（最上位ビット）は常に0である。この性質は、多バイト文字コードと併用する場合に重要になる。
ICTにおける「文字」には、一般通念では文字でないものも含まれている。たとえば、SP(0x20)は空白文字である。2バイトコードの全角空白と区別して半角空白と呼ばれる。これがないと、文字列中に間隔を開けられず、英単語さえ区切れない。
また、赤字で書かれた33種類の「文字」は、コンピュータやネットワークを制御する制御文字である。プログラミングでは、以下のものだけ知っていれば十分だ。

NUL(0x00)
ヌル文字。「ヌル・ターミネータ」として、文字列などの終わりを示す
HT(0x09)
水平タブ。タブストップ位置までカーソルを右に進める
NL(LF:0x0a)
改行（ラインフィード）。Linux系OSではNLのみで改行を表す
CR(0x0d)
キャリッジリターン。カーソルを先頭位置に戻す。WindowsではCR+LFの2BYTEで改行を表す
SO(0x0e)
シフトアウト。「7ビット文字しか使えない環境で、半角カナ文字の終わりを宣言する」のが元々の機能だが、JISとASCIIの文字を混用する際にも用いられ、JIS文字列の終わりを意味する
SI(0x0f)
シフトイン。「7ビット文字しか使えない環境で、ASCIIから半角カナ文字への切替を宣言する」のが元々の機能だが、JISとASCIIの文字を混用する際にも用いられ、JIS文字列の始まりを意味する

演習：英数字文字列のコード化

【授業フォルダにワークシート「文字情報演習.txt」がある】
テキストエディタ上で、自分の名前をアルファベット表記した文字列を、ASCIIコード（列）に変換しよう。 


例：
Y    O         Y    A    M    A    N    O    G    U    C    H    I    \0(NUL)
0x59 0x4f 0x20 0x59 0x41 0x4d 0x41 0x4e 0x4f 0x47 0x55 0x43 0x48 0x49 0x00
この14文字の文字列（半角空白を含む）は、14 + 1 = 15 BYTEのBYTE列で表現される。ASCIIコードという「文字の規格」がまずあり、その上にASCIZ文字列※11という「文字列の規格」が成立するわけだ。

11　あまりセンスのよいネーミングではない。0で終端されたASCII文字列というダジャレ。

文字列(string)は文字の並びであり、典型的には「。」で区切られた1つの文や、改行で終わる1つの段落である。テキストファイル全体（たとえばPythonのプログラム）も、改行コードなどの制御文字を含んだ1つの文字列である。
Pythonプログラミングでは、この文字列(string)が主要なデータ型の1つであり、後に学ぶように、多くの文字列操作機能がある。

Shift_JIS文字コードとUnicode

日本語文字コードは多BYTEコードであり、上記のような種類があるが、この節ではWindowsのテキストファイルで広く使われているShift-JISについて説明する。Shift_JISコード表は6000文字以上を収録した巨大なもので、ASCII文字のように図を掲載できないが、Windowsツールの文字コード表で調べられる。図1-6にその画面と使い方を示す。①～⑤の順に操作すれば、ある文字のShift_JISコードとUnicode（符号位置）を同時に調べられる。

図1-6: 文字コード表の画面と使い方

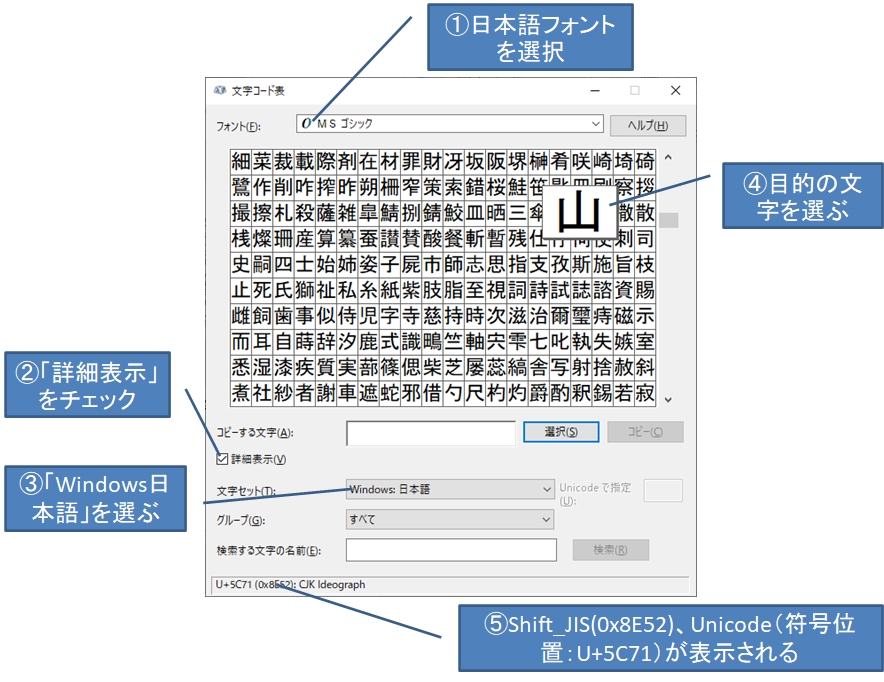
図は「山」の文字コードを調べているところだ。

12　Unicodeとその文字符号化スキーム（UTF-8など）は、国際標準規格ISO/IEC 10646で定義されている。「文字符号化スキーム」を詳述する余裕はないが、「山」のUnicodeコード（符号位置）「U+5C71」というのはいわば「文字コード表のマス目番号」であり、そこからメモリ上の実際のバイト列への変換方式を「文字符号化スキーム」と考えると少しは分かりやすい。ちなみに「UTF-16 Big Endian」では「0x5C71」とそのままだが、「UTF-16 Little Endian」だと「0x715C」と反転するし、「UTF-8」だと「0xE5B1B1（3バイト）」というように、一見無関係に見えるくらい変形される。

Shift_JISコードは、国際標準規格※13であるJISコードの第1バイト（上位バイト）をずらして（シフトして）、MSBが常に1になるようにしたものである。このため、MSBが常に0になるASCII文字コードと自由に併用できる性質を持っている。第2バイトはASCII文字コードと衝突するが、第1バイトのMSBでコードを判別できるからだ※14。 これに対してJIS文字コードは、第1バイト、第2バイトともASCII文字コードと衝突するため、原理的にASCII文字コードと判別できない。したがって相互の切り替えには、制御文字SIとSO（前述）が用いられる。たとえば、 


ABC[SI]漢字だよ[SO]123
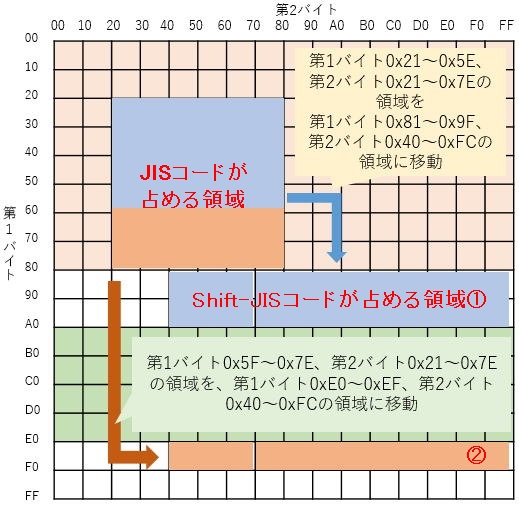
という具合だ。これだとプログラム上の処理がたいへん煩雑になる。ちなみに、Shift-JISの「シフト」と、SI・SOの「シフト」は無関係である。
図1-7に、JISコードとShift-JISコードの関係を示す。JISコードからShift_JISコードへの変換は、文字の並びを変えずに領域ごとシフトさせるだけなので、簡単な数式で計算できる。

13　JISコードは、ASCIIコードと同一の1BYTEコード（英数字、半角カタカナ、記号）が日本工業規格(JIS)のJIS X0201で、漢字・かな・カナなどの全角文字がJIS X0208で、また国際標準規格ISO-2022-JPでも定義されている。Shift-JISコードは、長らく標準化対象外のデファクトスタンダードだったが、現在はJIS X0208またはJIS X0213の「附属書1」として一応の標準化がなされており、その意味でShift-JIS X 0213ともいう。文字コードの標準化をめぐるテーマはたいへん複雑かつ深遠なので、この授業ではこれ以上深入りしない。

14　2バイト文字コードには目もくれないアメリケーンなアプリでは、それでも文字が化け、第2バイトが\(0x5c)とかぶる文字（たとえばソ：0x835c）以降が正常に表示されなかったりする。

図1-7: JISコードとShift_JISコードのコード領域の関係

幸い、多バイト文字に独自の制御コードはなく、ASCII文字コードの制御コードが流用される。つまり、多バイト文字は一般にASCII文字コードとの混用を前提に作られている。例外はUnicodeで、ASCII文字コードの定義を内包しているので、Unicodeだけですべての文字列を記述できる※15。

15　繰り返しになるが、Pythonでは、プログラムはUnicode(UTF-8)を用いて記述するよう決められているので、テキストエディタ上でプログラムを書く場合には、「保存」時に文字コードの指定に注意すること（この授業で使うGoogle Colabの場合は特に意識しなくてもよい）。

演習：日本語文字列のコード化

自分の名前を全角文字列で表記し、Shift-JISとUnicode(符号位置)に変換しよう。文字コードは文字コードツールで調べること。 


例：
山     之     口            洋     \0(NUL)
0x8e52 0x9456 0x8cfb 0x8140 0x976d 0x00      Shift_JISコード
0x5c71 0x4e4b 0x53e3 0x3000 0x6d0b 0x00      Unicode(符号位置)コード
この5文字の文字列は、どちらの文字コードでも、5 * 2 + 1 = 11 BYTEのBYTE列で表現される（UTF-8の場合は5 * 3 + 1 = 16 BYTE）。これらもまたASCIZ文字列と呼ぶ。