step03 条件分岐と反復処理
前stepのサンプルプログラムでは、実行の流れは上から下への一直線であり、自然、できることも限られていた。条件分岐(ブランチ)と繰り返し(ループ)の構文を学ぶと、実行の流れが自由に制御でき、実現できる処理がはるかに広がる。
このstepでは、いくつかの数値計算を課題に、pythonプログラムの表現を考えてみよう。
サンプルプログラムの内容は、一部を【 空欄 】にしてある。各自、空欄の中身を考えて、プログラムを完成させてほしい。これは、サンプルプログラムで言語の文法を学ぶ段階から、要求仕様をプログラムとして書くという次の段階への、いわば準備運動だ。
奇数か偶数かを調べる
冒頭で変数nに代入された整数が奇数か偶数かを判定する。それだけのプログラムだが、2通りの場合分けがあり、それぞれで動作が違う。サンプルプログラムをリスト3-1に示す。【 空欄 】には、変数nを2で割った余り(剰余)を変数amariに代入する処理が書かれるはずである。
偶奇を調べる整数、つまり対象データは、3行目で代入されている変数nである。nは【 空欄 】の処理で奇数か偶数かを調べられ、もし偶数ならamariは0となって、if文以下、つまり7行目が実行される。もし奇数ならelse文以下、つまり9行目が実行される。どちらも実行されなかったり、両方が実行されることはない。これを排他処理という。学校数学では場合分けと呼んでいた。
したがって、このプログラムをテストするには、少なくともnに偶数、奇数の両方を代入して、2回実行しなければならない。このようなテストデータの集合をテストセットと呼ぶ※1。
1 このような単純なプログラムならともかく、複雑で大規模なシステムでは、テストセットの設計はたいへん難しい。まれな条件が重なって、今までに1度も実行されていなかったコードが実行され、そこに潜んでいたバグから大きなトラブルに発展した例はたくさんある。
「if 《条件式》:」や「else:」の最後につけられたコロン(:)に注意しよう。これは、条件式が成立したときに実行されるブロック(複数行にわたる実行文の集合)、非成立の場合に実行されるブロックの始まりを意味する。それぞれ、- ifブロック
- elseブロック
多くの言語において、実行ブロックは中括弧{}で囲むことで明示されるが、python言語の流儀はやや風変わりで、行頭からのインデント(字下げ)でブロックを明示する。つまり、他の言語のように、単にプログラムの見やすさのためのインデントではなく、厳密な文法的な意味を持ったインデントなのだ。このインデントには、タブ(TAB)文字を使ってもよいが、pythonコミュニティーでは半角空白4つを使うよう推奨されていて、正直やや面倒くさい※2。
2 この変わった言語仕様は、「どのプログラマが書いてもコードが大体おなじ姿になる」ことを目指して決められたそうだが、果たして効果はあるのだろうか。ここだけの話、「一生涯使い続けます」と神に誓えば、秀丸で4カラム分に設定したタブを使ってもいいかもしれないと、密かに思っている。Pythonの生みの親であるGuido van Rossumのバイブルにも、インデントはスペース4つとし、タブは使わないと厳かに書かれてしまっているので、私の神は異端の神なのかもしれない。
うるう年の判定
一般に、場合分けの数は2つとは限らない。うるう年を判定するロジックは、西暦年を4通りに場合分けすることで成り立っている。だから最終的には4分岐が必要だが、if構文によるpythonの分岐は、条件式(値が真(true)または偽(false)のどちらかである論理式)を分岐の基準にしているから、1度には2分岐しかできない。
したがって、4分岐を実現するには、「if~else」構文を3つ、段階的に連続で※3使うしかない。サンプルプログラムをリスト3-2に示す。
3 これを「カスケード(cascade)状に」という。casecadeとは、階段状に流れる滝のことだそうで、洋風の庭園建築なんかでよく見られるアレだ。
こうした多段の分岐構文では、ifとelseだけを使うと、pythonの文法とも相まって、インデントがどんどん深くなってしまう。そこで「elif 《条件式》:」が使われる。これは、
else:
if 《条件式》:
このような多段階の判定では条件のきつい方から順に判定するのが鉄則である。この「うるう年」の場合なら、「西暦が400で割り切れる」最もレアなケースを先にテストする。でないと、後からつぎつぎに発生する例外の処理に追われてしまう。
例によって3行目で、判定すべき西暦という対象データを直接書いているが、これだと異なる西暦をテストするときに、いちいちプログラムを書き換えるしかなく、まったく実用的ではない。だがそれも、step05で、コマンド行からデータを渡す方法を学ぶまでの辛抱だ。
論理演算子(andとor)
if文は条件式の真偽値によって2通りの分岐しかできないと書いたが、条件式自体を複雑なものに書き換えることで、同じロジックを2分岐で済ますことは可能である。
pythonには、多くのプログラミング言語と同様、論理演算子が用意されている。これは単純な論理式を2つつないで複雑にする働きをもつ2項演算子である。
リスト3-3は、リスト3-2と同じ「うるう年」の判定プログラムを、論理演算子を使って2分岐に書き換えたものだ。
andは日本語のかつ、orはまたはを表す。だから、この論理式は、「西暦が4で割り切れないか、または、西暦が100で割り切れてかつ400では割り切れない(とき、うるう年でない)」ことを表現している。
このように、andとorが混在しているときには、andはorより先に計算される。昔、小学校で習った、×は+より先に計算するという規則と同じだ。orをandより優先させたい場合は( )で囲むのも、四則演算と同じである※4。
4 そのためかどうか、andを論理積、orを論理和と呼ぶ。
階乗の計算
つぎは、同じ(ような)処理を何度も行う繰り返し(ループ)構文について学ぶ。
そもそもプログラムは、たくさんのデータを一挙に処理するために作られるものなので、一直線のプログラムはあまり実用的ではない。そこで、たくさんのデータを「次から次へと処理する」ために、繰り返し構文が必要になる。つまり、はじめて、私たちのプログラムの同じ行が2回以上実行されることになる。
プログラムの処理は同じでも、扱われるデータはもちろん異なる。そうでなければ繰り返して計算する必要はない(もちろん、イルミネーションの点滅とか、繰り返すこと自体に意味がある制御プログラムは例外だ)。
ここでは、階乗(power)の計算を扱う。ある整数の階乗とは、1からその整数までのすべての整数を掛け合わせた数のことだ。整数nの階乗をn!と表し、たとえば
5! = 5 * 4 * 3 * 2 * 1 = 120
問題:40-32÷2=?
小学生「4!」
理系「よくわかってんじゃん」
文系「やっぱわかんないか~w」
このプログラムでは、階乗を求める数を3行目でnに代入し、階乗を作る変数powerに初期値1、ループ変数iに初期値2を代入している。そして、iを1ずつ増やしながら、powerにiをかけ込んでゆく。
ループから抜け出すのは、iがnより大きくなり、while文の条件式が成立しなくなった時で、実行点は最終行に飛び、階乗の計算結果を出力して終わる。図3-1にプログラムの実行結果を示しておこう。これを見ると、pythonが、4バイトなどの制限を超えた巨大な整数を扱えることがわかる(どのように実現されているのかは、私たちユーザが知る必要はない。
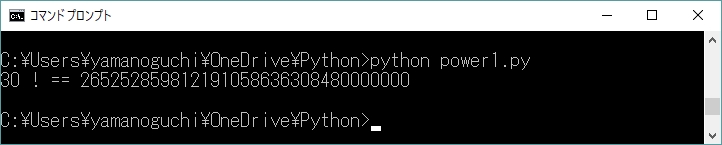
while構文は、ほとんどのプログラムにおける繰り返しの基本である。しかし、繰り返しには、ループ変数の初期化(i = 2)や、ループ毎の後処理(i += 1)といった処理がつきものである。これらをまとめて記述できれば、プログラムはもっと効率よく書けそうだ。
そこで用意されたのがfor構文である。これを用いれば、リスト3-4のプログラムは、リスト3-5のようにすっきりする。
新しい制御構造を使えるようになると、プログラムは簡略化されて短くなり、その分バグを作り込むリスクも減る。
5 range(start, end, step)は、整数startから始まり、step刻みで、end - 1までの整数を順に生成するジェネレータである。ちょっと難しいのだが、あらかじめリストやタプルを生成するのではなく、次々に生成(generate)した値をiに渡してゆく仕組である。この方式ならば、無限に続く列でも生成できるわけだ。
素数の判定
条件分岐と繰り返しを組み合わせることで、どんなに複雑なロジックも表現できる。
ここでは、数が素数かどうかを調べるプログラムを考えよう。冒頭で代入された「n」が、調査対象の整数である。
素数とは1とその数自身しか約数を持たない整数だから、2から始めてしだいに大きな数で割ってみれば、判定できる。途中のどこかで割り切れれば素数ではないし、最後まで割り切れなければ素数だ。このナイーブな発想を形にしたのがリスト3-6である。
import mathは、数学関数モジュールを参照している。平方根関数sqrt()を使うためである。モジュールは他の言語のライブラリに相当するもので、pythonコードをまとめたファイルだ。このように、python処理系自体にはない機能も、各種モジュールをimportするだけで使える。どんなライブラリがあるのかは、step01で少しだけ紹介したが、Webで調べれば便利なモジュールがたくさん見つかるはずだ。
除数(div)の上限はなぜここまでよいのか、考えよう。
初出のbreakは、whileやforループからただちに抜け出すことを示す※6。
このアルゴリズム(計算手順)があまり効率的でないことは、考えればわかる。たとえば、2で割れなかった数を4で割ってみるのは無駄だ。もう少し効率的に書けないものだろうか。
6 最近はあまり見かけないが、以前は巨大迷路という施設があちこちにあって、抜け出すには小一時間かかる。ただ、気分が悪くなったとか、子どもがオシッコに行きたくなった場合は、手を挙げてギブアップすると、どこからともなく係のお姉さんが現れて、根性無しの出口から外に出してくれた。breakはいわば、プログラム版「根性無しの出口」だ。ただし、脱出できるのは、一番内側のループだけである。
1から100までの素数をリストアップする
続いて、上のプログラムを少し発展させて、1から100までの素数をリストアップするプログラムを考えよう。リスト3-6のアルゴリズムで、ある数が素数かどうかを判定することを、調べる数をインクリメントしながら99回も繰り返している。リスト3-7にプログラムを示す。
for構文の威力で、プログラムはずいぶん簡潔に書ける。特に最後から2行目のelse:に注目。これはifに対応するものではなく(インデントのレベルが違うことに注意)、実は内側のfor構文に対応しているのだ。このelseブロックはfor構文からbreakしなかった場合にのみ実行される。他の言語にない構文なので最初はとまどうが、慣れればたいへん便利である。この構文がない言語では、素数だった(割り切れた)ことを示すフラグ変数※7を立ててbreakし、ループの外で、フラグ変数を調べてループから出てきた原因を特定するといった、余計な処理が必要になる。
それにしても、処理効率は依然としてたいへん悪い。全体の構造は2重ループであり、内側のループの効率(というか、非効率さ)はリスト3-6と同じであり、それに加えて、すでに素数と判明した数の倍数(たとえば、3に対して6や9など)まで、しらみつぶしに調べており、非効率さ自体もいわば2重ループになっている。
7 フラグ変数は、真(通常は1)か偽(0)を値とする変数。なにかのイベントが発生したときに、それを記録するために立てる(真にする)。「2ちゃんねる」でよく使う「死亡フラグが立ちました」というのがそれ。
実は、リスト3-6やリスト3-7を改良して、効率を大幅にアップするには、多数のデータを格納できるリストという仕組みが欠かせない。つぎのstep04でリストについて学んだ後に、素数の問題について再考しよう。
非効率性の確認
リスト3-7のプログラムの非効率性を確かめるために、つぎの実験をすること。調べる数の上限を100000や1000000にして、実行時間を測定する。ついで、1000000の時には、100000の時の10倍ではなく、はるかに多くの時間がかかることを確かめること(非線形性の確認)。