コンピュータ機械工学

第9回近似法

9.1 概要

多数のデータの集合の傾向を、ノイズなどの影響を考慮して方程式で表すことを近似法という。
補間法と異なることに注意せよ。
数学的には、最小二乗法に基づいている。

9.2 最小二乗法

最小二乗法は、(x₁,y₁), ・・・, (x_n, y_n) というn個のデータ点が与えられたとき、これらを近似する方程式として

というm次多項式 (m<n) を考え、この方程式と測定データとの距離の二乗和

が最小となるように係数 a₀ ・・・ a_m を決めるものである。
距離の二乗和 E が最小となるとき、E を a_j によって偏微分した値はすべての a_j に対して 0 となる。すなわち、

a₀について偏微分すると

同様に

9.3 プログラム・コーディング

以上より、近似多項式の係数a₀ ・・・ a_m を求めるには、以下の (m+1)元の連立方程式を解けばよい。

この連立方程式をガウス消去法やガウス・ジョルダン法などを用いて解く。次の係数行列を作る。

この係数行列は斜め方向に同じものが並んでいるのですべての要素を計算しなくとも良いことがわかる。

注意

べき乗計算(x^yの計算)について、C言語の math.h には double pow(double x, double y) という関数が用意されているが、この関数は x が 0 のときにエラーメッセージの様なものが出てしまう。これを回避するため、今回の課題では以下のような関数を定義して利用すると良い。
```
double ipow(double p,int n)
// べき乗計算
{
	double s=1;
	for (int k=0; k<n; k++) s *= p;
	return s;
}
```

9.4 例題

最小二乗法を用いて、以下のデータに対する近似多項式の係数を求め、画面に出力せよ。近似式の次数は m = 2, 3 および 5 とすること。また、得られた近似関数 y=f(x) について、-3≦x≦3 における y=f(x) の値を、x の刻み幅を0.1として出力せよ。
```
補間対象となるデータ(7点)
(x, y) = 
-3.0  -3.0
-2.0  -0.8
-1.0   1.2
 0.0  -3.2
 1.0   2.5
 2.0   2.0
 3.0   3.8
```
なお、y=f(x)の値を出力する計算のヒントは、以下のとおり。

9.5 課題 (提出〆切：金曜日22時)

最小二乗法は、独立変数のべき乗を説明変数とする重回帰分析の一種であるとみなすことができる。そこで、重回帰分析で用いられる決定係数 R² によって、近似式の精度を確認する。
計測データ measurement_data.csv を最小二乗法により近似し、決定係数を算出するプログラムを作成せよ。決定係数 R² の定義式は以下の通りであり、決定係数の値が1.0に近いほど近似式の精度がよいことを意味する。

ここで、N はデータ点数、y_i は計測値、y'_i は推定値である。または y_i の平均値である。
課題の進め方
- 提出ファイルは"9_1.cpp"とすること。
- ファイルには、1列目に入力 x のデータ、2列目に出力 y のデータが記録されている。ファイル名はプログラム内で指定すること。また、データ点数は事前には分かっていないという前提で動作するプログラムを作成すること。先週の課題を参考にするとよい。
- 次数が 1~10 の場合について近似式を求め、その数式を用いて入力 x に対する推定値 y' を計算し、それらを元に決定係数 R² を算出せよ。画面には各次数に対する決定係数の計算結果を出力すること。
- 実行例は以下の通りである。値は適当であるため注意すること。
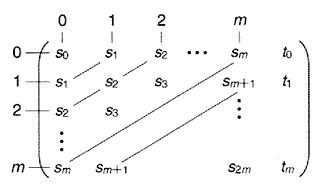
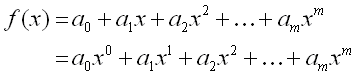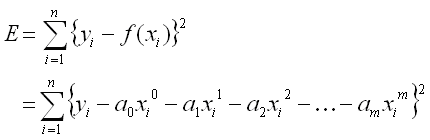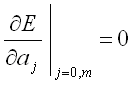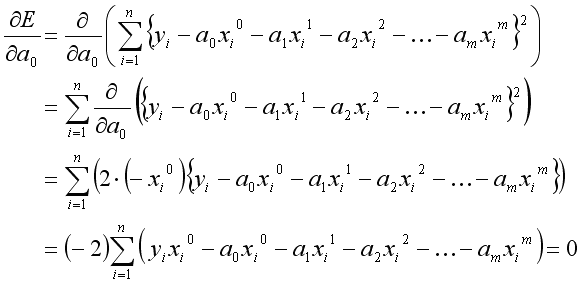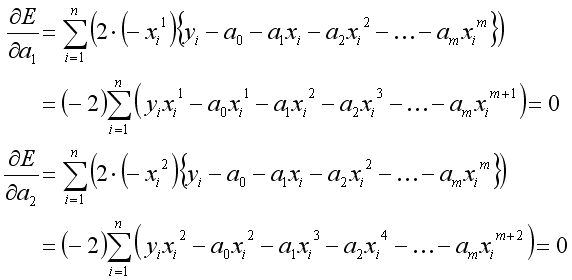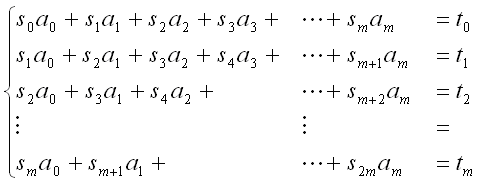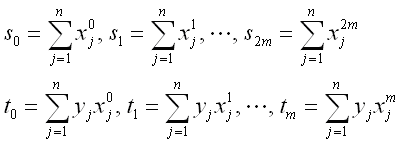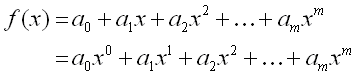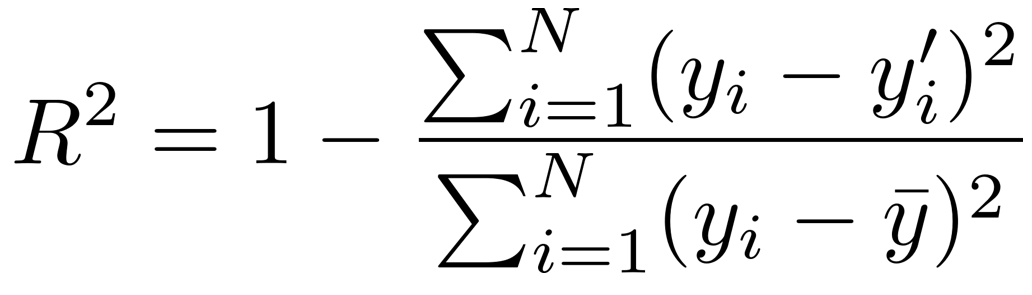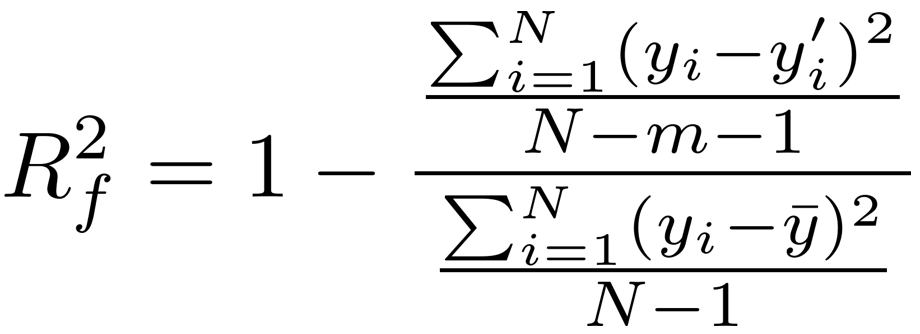課題1で求めた決定係数は、近似曲線の次数が増えるほど1.0に近づいていく性質がある。そのため、重回帰分析で用いられる自由度調整済み決定係数 R²_f により、次数の影響を考慮する。課題1で作成したプログラムを改良し、自由度調整済み決定係数の値が最大となる近似式の次数を特定するプログラムを作成せよ。自由度調整済み決定係数は次式で定義される。

課題の進め方
- 提出ファイルは"9_2.cpp"とすること。
- 課題1と同じ計測データファイルを用いること。
- 各次数に対する自由度調整済み決定係数の計算結果を画面に出力すること。
- 実行例は以下の通りである。値は適当であるため注意すること。

第9回 近似法