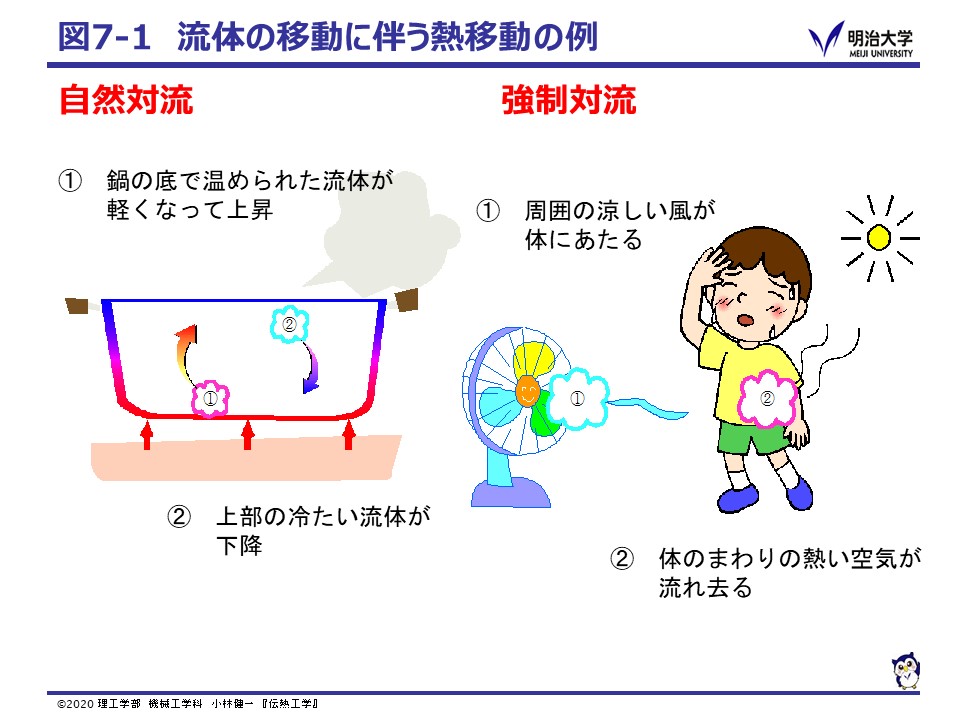
空気や水などの流れによって熱エネルギーが運ばれる現象を対流熱伝達(Convective heat transfer)と呼びます。
鍋で暖められるている味噌汁のように温度差に起因して流れが自然に生じる場合を,自然対流(Natural convection, Free convection),扇風機にあたる場合のように外からエネルギを与えて流れを起こす場合を,強制対流(Forced convection)と呼びます。

対流熱伝達による熱流束 q W/m2 は,ニュートンの冷却法則より,高温部の温度 THと低温部の温度 TLの差に比例します。
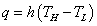
ここで,比例定数 h W/(m2・K) は熱伝達率 (Convection heat transfer coefficient) で,この値が大きいほど熱エネルギーがよく伝わります。
熱伝達率は,熱伝導率のような物質固有の物性値ではありません。 扇風機で涼んでいるときに,風力を弱から強に切り替えるとより涼しく感じますが, これは,人とまわりの空気の温度差が同じでも,風力を変化させることにより熱伝達率が大きくなり,熱流束が大きくなったと説明できます。 このように対流熱伝達率の大きさは,熱を運ぶ流体の種類のみならず,流れの状態に影響を受けます。 流れの状態は,流れの駆動源,流れの形態,層流か乱流かなどの組み合わせで分類され, 多くの場合,自然対流より強制対流,,そして,相変化を伴う沸騰・凝縮の方が多くの熱を伝えることができます。

最も基本的な場であり,かつ,様々な場面に応用のできる,平板に沿う流れによる強制対流熱伝達について,まず勉強しましょう。
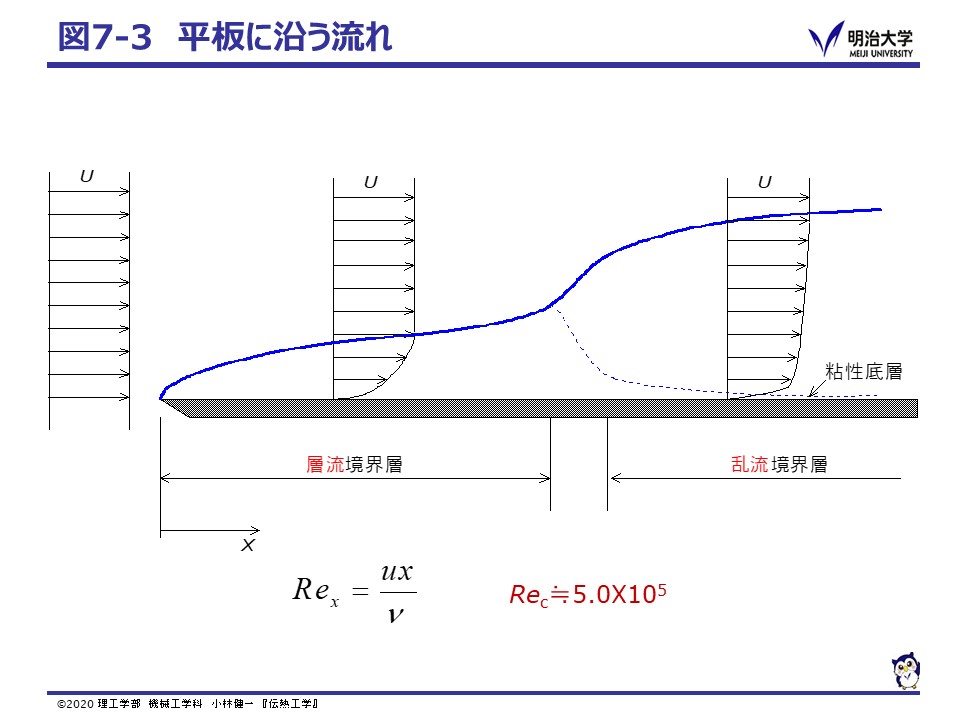
流れに平行に平板が置かれた場合,流体と平板の間には粘性(Viscosity)が働き,平板上では速度がゼロに, また,平板のまわりには主流よりも速度が遅い領域ができます。 この主流と平板の間の領域のことを,境界層(Boundary layer)とよび,粘性の影響を強く受けます。 境界層は,平板の先端から流れの方向へ向かって次第に厚く発達していきます。 先端からある距離までは,境界層内に速度の乱れがない層流(Laminar)境界層であり, 平板に沿って流れていくに従い境界層内に速度の乱れが生じ乱流(Turbulent)境界層へと変化していきます。 層流か乱流か,どこで遷移するか等の目安には,平板先端からの距離 x を代表長さとしたレイノルズ数(Reynolds number)を用います。
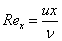
平板に沿う流れの場合,主流の状態にもよりますが Rex = 5.0X105 程度で,層流から乱流へと遷移します。
流れに平行に加熱(流れより高温)された平板が置かれた場合について考えよう。
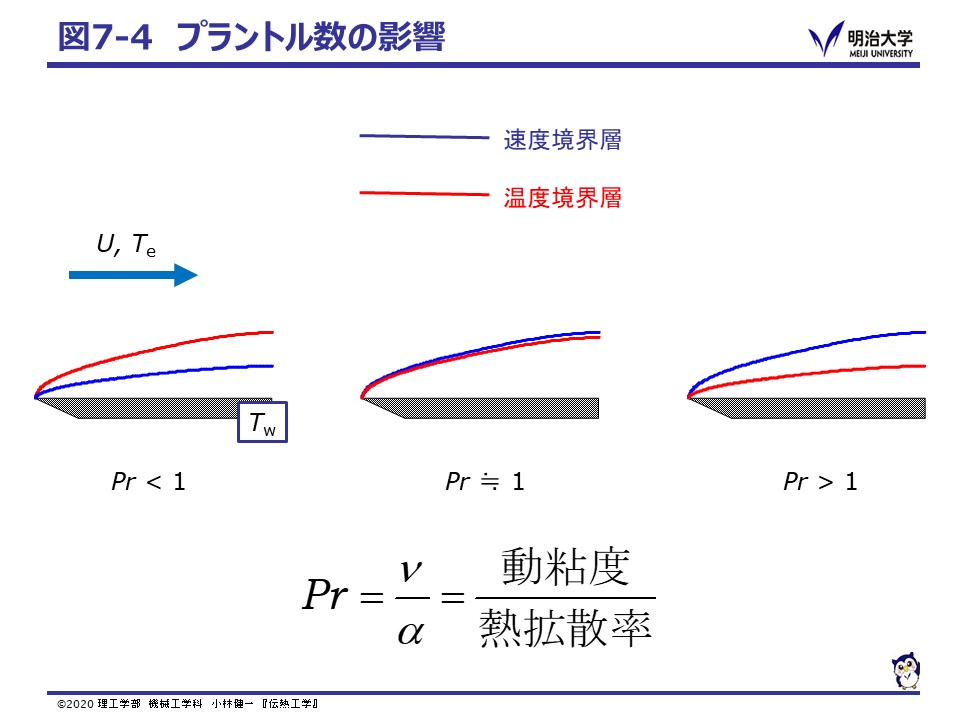
流体の場合と同じように,平板の温度の影響を受け,平板の温度(Tw)と主流の温度(Te)の間の温度になる領域が形成されます。
この主流の温度と平板の温度の間の温度の領域のことを,温度境界層(Thermal boundary layer)とよび,
速度境界層と同様に平板の先端から発達します。
温度境界層と速度境界層の厚さは相似関係にあり,動粘度 ν と熱拡散率 α (ともに単位は m2/s)の比の無次元数プラントル数(Prandtl number)により厚さの比を表します。
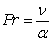
熱伝達率を求めるためには,流れの状態を把握する必要がありますが,そのためには流れの運動方程式(ナビエ・ストークスの方程式)を解かなくてはなりません。 流れの運動方程式を解析することは,計算機の発達した現在でも大きな計算負荷が必要で簡単ではありません。 そこで,いくつかの代表的な状況について,熱伝達率と流れの状態を表す無次元数との関係式(相関式)が提供されています。 熱伝達率に影響を与える因子を無次元数にするのは,たとえば,全長 10 cmで流体が 50℃の水の場合など, ある特定なケースだけで成り立つ関係とするのではなく,広く一般に活用できる様にするためです。 そこで,熱伝達率の無次元数としては,ヌセルト数(Nusselt number)を用います。
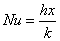
ここで,ヌセルト数とビオ数は,定義式の形が同じですが,ヌセルト数の熱伝導率には,ビオ数の場合と異なり流体の熱伝導率を用います。
平板に沿う速度境界層,温度境界層は,平板先端から発達します。
このため,各無次元数の代表長さには,平板の先端からの距離 x を用いました。
ここで,ある座標 x における熱伝達率を,局所(local)熱伝達率,そのときの無次元数を,局所ヌセルト数と呼びます。
一方,平板全体からの平均的な様子を知りたい場合は,平板の全長 L を代表長さとし,
平板前面の平均熱伝達率を,平均(average)熱伝達率,そのときの無次元数を,平均ヌセルト数と呼びます。
| 流れの状態 | 局所 | 平均 |
|---|---|---|
| 層流 | 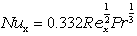 |
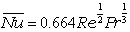 |
| 乱流 | 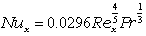 |
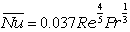 |
| 流れの状態 | 局所 |
|---|---|
| 層流 | 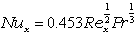 |
| 乱流 | 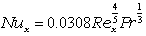 |
流れの中に置かれた物体が加熱されている場合,それぞれの流れの様子をスケッチし,一番冷えると思われるポイントに☆マークをつけてみよう。
2021.03.08 更新