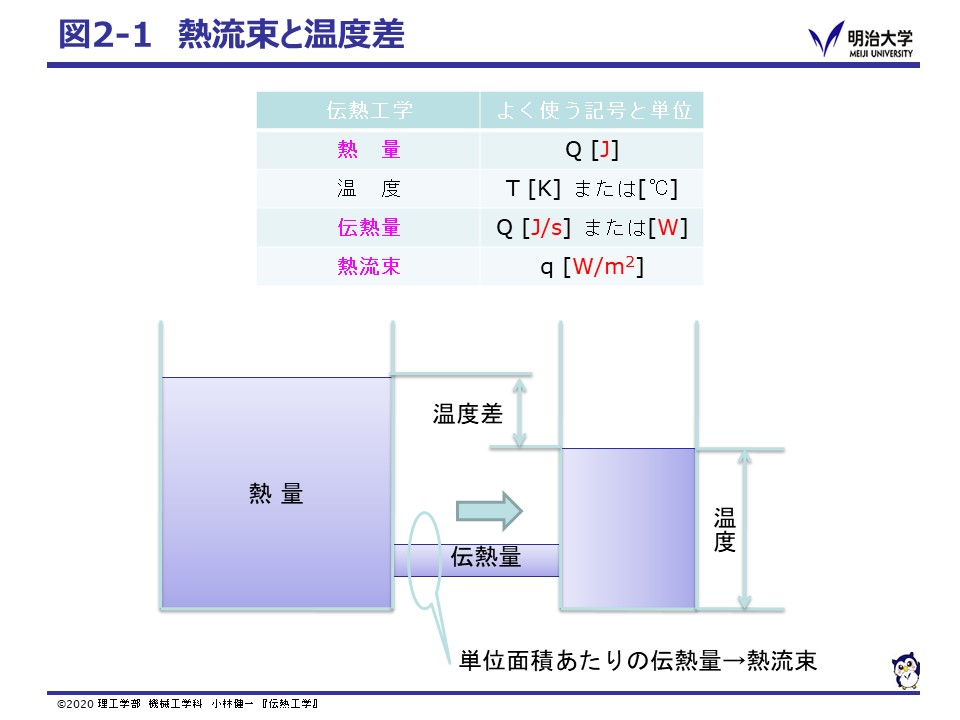
水の流れでは,圧力と流量の関係,電気の流れでは,電圧と電流の関係が基本ですが,同じ移動現象である伝熱では,温度差と熱流束 q にどのような関係があるかが重要となります。 温度差と熱流束の関係は,伝熱形態ごとに異なるので,三つの熱エネルギーの伝わり方それぞれについてこの関係を見ていきます。

物体内に温度勾配が存在すると,高温部から低温部へ熱伝導(Conduction) により熱エネルギーが移動します。 このとき,熱流束 q W/m2 は,フーリエの法則より次のように表されます。
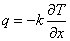
ここで,k W/(m・K) は熱伝導率 (Thermal conductivity) で,物質によって定まる物性値です。
熱エネルギーは温度の高いところから低いところへ向かって伝わるので,熱エネルギーの伝わる向きを正とすると温度勾配は負となります。
このため,式(1)の右辺にマイナスがつきます。
温度勾配が等しい場合,熱伝導率 k の値が大きいほど熱流束 q の値も大きくなり,熱伝導率が大きいと熱エネルギーがよく伝わり,熱伝導率が小さいと熱エネルギーを伝えにくいことがわかります。
熱伝導率を表す記号には,k を用いていますが,λ も一般には広く用いられています。
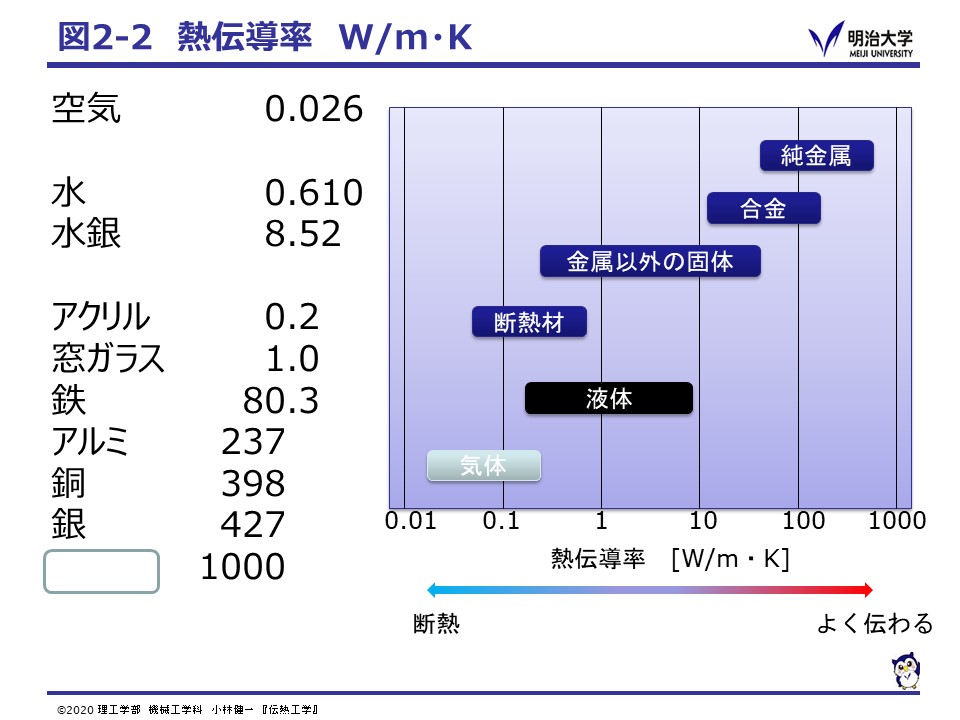
代表的な物質の熱伝導率を見てみよう。
一般に,金属は熱伝導率が大きく熱エネルギーを良く伝えます。
これは,金属内では自由電子の移動により熱エネルギーも運ばれるためで,よく電気を伝える物質は熱エネルギーもよく伝えます。
樹脂や木材など金属以外の固体は自由電子をもたないため,金属に比べ熱伝導率が小さく熱エネルギーを伝えにくくなります。
熱伝導率が大きい固体は,電気もよく伝える場合がほとんどですが,ダイヤモンドだけは例外で熱伝導が非常に大きいにもかかわらず,電気の絶縁体です。
液体や気体も熱伝導により熱エネルギーを伝えますが,固体に比べて熱伝導率は小さくなります。
特に空気は,熱エネルギーを伝えにくい物質で,様々な場面で断熱のために用いられます。
また,断熱材は熱エネルギーをまったく伝えないわけではなく,熱伝導率が非常に小さい熱エネルギーを伝えにくい物質のことを呼びます。
空気中や水中などで,流れにのって熱エネルギーが移動する現象を対流熱伝達 (Convective heat transfer)と呼びます。 対流熱伝達による熱流束 q W/m2 は,ニュートンの冷却法則に従い高温部の温度 THと低温部の温度 TLの差に比例します。。
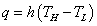
ここで,比例定数 h W/(m2・K) は熱伝達率 (Convection heat transfer coefficient) で,熱伝導率と同様,大きい場合は熱エネルギーがよく伝わり小さい場合は伝わりにくくなります。 熱伝達率を表す記号には h を用いていますが,κ も一般には広く用いられています。
熱伝達率は,熱伝導率のような物質固有の物性値ではありません。
たとえば,扇風機で涼んでいるときに,風力を弱から強に切り替えるとより涼しく感じますが,これは,人とまわりの空気の温度差が同じでも,風力を変化させることにより熱伝達率が大きくなり,熱流束が大きくなったと説明できます。
このように対流熱伝達率の大きさは,熱を運ぶ流体の種類のみならず,流れの状態に影響を受けます。
流れの状態は,流れの駆動源,流体の種類,層流か乱流か,そして,相変化の有無などの組み合わせで分類されます。
扇風機の例のように,外からエネルギを与えて流れを起こす場合を,強制対流(Forced convection),真夏の舗装道路の上に立ち上る陽炎のように,温度差に起因して流れが生じる場合を,自然対流(Natural convection, Free convection)と呼び,多くの場合,自然対流より強制対流の方が多くの熱を伝えることができます。
物質が固体・液体・気体の間で状態変化することを相変化といい,特に液体から気体への気泡の発生を伴う相変化のことを沸騰といいます。
沸騰では,相変化をするときに熱を吸収・放出する(潜熱)のに加え,気泡によるかく乱などによって非常に大きな熱エネルギーを伝えることができます。
熱伝達率を求めるためには,流れの状態を把握する必要がありますが,そのためには流れの運動方程式(ナビエ・ストークスの方程式)を解かなくてはなりません。 流れの運動方程式を解析することは,計算機の発達した現在でも大きな計算負荷が必要で簡単ではありません。 そこで,いくつかの代表的な状況について,熱伝達率と流速・代表長さ・流体の種類との無次元の関係式(相関式)が提供されています。

太陽から地球へ熱エネルギーが伝わるように,熱伝導や対流熱伝達により伝える物体が存在しない真空中でも,熱エネルギーは電磁波として伝わります。 この形態の熱移動は,ふく射伝熱 (Radiation) と呼びます。
絶対温度がゼロでない物体は,内部エネルギーを電磁波の形で放出します。 理想的な放射体である黒体(Black body)の場合,放射されるエネルギーは絶対温度 T Kの4乗に比例します。
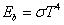
ここで,σ はステファンボルツマン定数で,5.67×10-8 W/(m2・K4) の一定値です。放射を扱う場合,温度には絶対温度を用いることに気を付けてください。
二つの黒体(T1 K,T2 K)間のふく射による伝熱量は,それぞれの絶対温度の4乗の差に比例し,真空中では光速(3×108 m/s)で高速に伝わります。
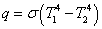
実際の物体表面から放射されるエネルギーは黒体より小さな値で,その割合を放射率 (Emissivity) ε(0 ≦ ε ≦ 1)とします。
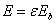
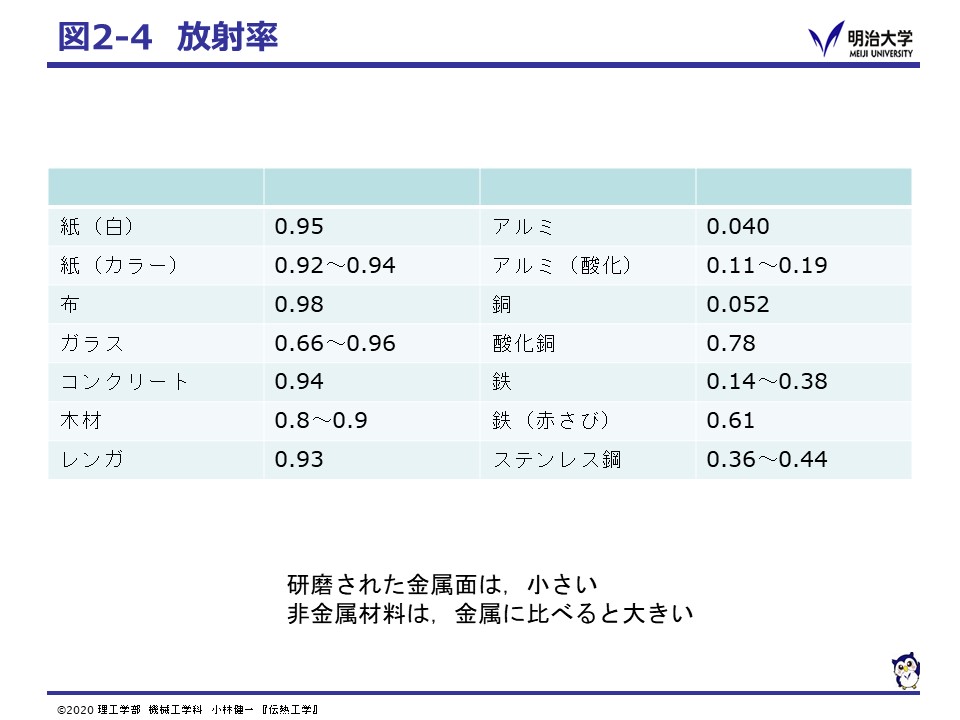
このときの,ふく射による伝熱量は,次の様になります。
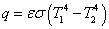
太陽の光が日陰に届かないのと同様に,ある物体表面から放出されたエネルギーは,すべてが他の物体表面に届くわけではありません。 また,同じ強度のエネルギーが降り注いでいても,エネルギーを受け取る表面の角度により受け取れる量が異なってきます。 放出されたエネルギーのうち,どれくらいが届くかは,形態係数(View factor) F(0 ≦ F ≦ 1)を用いて表します。
熱エネルギーの三つの伝わり方について,その概要を学びました。 実際には,熱エネルギーは熱伝導・対流熱伝達・ふく射伝熱の三つの形態のうち,単独,もしくは,組み合わさって伝わります。 それぞれの伝熱機構は異なるものの,単位面積当たりに熱エネルギーの伝わる量である熱流束 q W/m2 は,熱伝導率・熱伝達率・形態係数または放射率が大きいほど,大きくなります。
固体・液体・気体の熱伝導率の違いは,微視的なエネルギーの伝わり方で説明できます。 教科書・Web等で調べ,まとめて下さい。
2021.03.08 更新