ビークルダイナミクス特論

12/May/2025 1/4車体モデルによるシミュレーション(2)

1自由度モデル書き直し

以下は、1自由度振動系のプログラムを線形システムとしての記述を意識して書きなおしたものである。

変更した項目

微分方程式のパラメータを sim_1dof.m の本文中(=微分方程式を呼び出す側) で定義することにした。
- 先週までは、微分方程式の関数内 func_1dof (func_2dof)にて定義していた。この書き方では、出力ベクトルによっては微分方程式のパラメータを2箇所で定義する必要があった。前回ページ参照。
- 新しい書き方では、微分方程式を表す関数に、微分方程式のパラメータを渡す必要がある。
- ついでに、微分方程式を表す関数を sim_1dof.m の内部で定義することにした。
対象とするシステムを、関数 ss を用いて sys という変数に収めることにした。
- 状態方程式と出力方程式の両方が sys に含まれることになる。
- 例えば sys.A とすれば、行列Aを呼び出すことも可能。構造体の様にシステム行列を利用できる
- 実は、線形システムであればすべてこの形で微分方程式を定義できる。このため、関数名を func_ss と修正した。
入力を関数 u(t) とし、微分方程式に渡すことにした。
ついでにボード線図も出力させている。
- 但し、見栄えが悪いので以下で改良する。
%% としておくと、セルモードを利用可能。なお、ここではエディタ画面の見やすくするためだけにセルモードを用いている。

% sim_1dof.m を改良

%% 初期化
% ウィンドウを閉じる
clear;
close all;

%% 状態空間モデルを作成
m=1; c=1; k=10;

A=[0 1; -k/m -c/m];
B=[0; 1/m];
C=[1 0];
D=[0];

sys=ss(A,B,C,D);

figure(1);
set(gcf,'Position',[100 100 600 400]);
bode(sys);

%% ode関数の呼び出し
% 初期条件の定義
x0 =[0;0];
% シミュレーション時間の定義
time =[0:0.01:10];

% MATLABで関数を引数とする場合は、関数ハンドル@を利用する
% 4つめの引数はsolverのoption指定なので、ここでは空行列を定義したがお好みで
[t,x] = ode45(@(t,x) func_ss(t,x,sys,@(t) u(t)),time,x0,[]);    
    
% 数値積分結果を利用して出力ベクトルを算出
% 転置の操作が必要
% ode45の計算結果である t, x がどのようなサイズになるかを注意
y=(C*x'+D*u(t)')';

%% 入出力ベクトルを利用してグラフをプロット
figure(2);
set(gcf,'Position',[800 100 600 400]);

subplot(2,1,1)
plot(t,u(t));
ylabel('Force Input [N]');

subplot(2,1,2)
plot(t,y);
xlabel('Time [s]');
ylabel('Displacement [m]');

%% 状態空間モデルを利用した微分方程式の定義
function xdot = func_ss(t,x,sys,u)
xdot=sys.A*x+sys.B*u(t);
end

%% システムに対する入力を関数として定義
function ans = u(t)
% 入力をシミュレーション時間を表すベクトルとしているため
% 出力もベクトルとして定義する必要がある

% 強制振動の例
% ans = 10*sin(10*t);

% ステップ入力
% (for文を使っているのでいまいちカッコ悪い。もっとかっこよい書き方を募集中)
ans = zeros(length(t),1); % 入力ベクトルと同じ次数のゼロベクトルを作成

for i=1:length(t)
    if t(i)>1.0
        ans(i)=10;
    end
end

end

bode線図の見た目を良くする

MATLABで用意されているbodeコマンドを利用すると、ボード線図がrad/secでプロットされているが、これは機械の分野では一般的ではない。
そこで、以下のような方法で Hz に対しプロットする。ついでに見栄えも整える。
sim_1dof.m の bode(sys) の箇所を plot_bode(sys) に書き換えて実行せよ。

function plot_bode(sys)
% 少し見た目の整ったボード線図を描画

freq = logspace(-1,2,100); % 10^-1 ～ 10^2 Hz の範囲で、対数的に等間隔となる配列を生成

% 周波数領域は角周波数として与える必要があることに注意
[mag, phase, w]=bode(sys, freq*2.0*pi);

% 出力される多次元配列を1次元配列に
mag=squeeze(mag);

% ボード線図をプロット
loglog(freq, mag, 'color', [0.0 0.0 1.0], 'linewidth', 2.0);

% 見た目をきれいに
set(gca, 'FontName','Arial');
set(gca, 'FontSize',9);
xlabel('Frequency [Hz]');
ylabel('Gain ');

grid on;

end

1/4車体モデルによるシミュレーション(2)

上のサンプルプログラムをベースに、以下をパラメータとした上下二自由度系について検討せよ。

m1 = 30.0;   m2 = 300.0;
             c2 = 2500;
k1 = 180000; k2 = 30000;

入力：路面変位, 出力：ばね上変位としたときのボード線図を求めよ
入力：路面変位, 出力：ばね上加速度としたときのボード線図を求めよ
ばねのパラメータを k2 = 45000 および 60000 としたときのゲイン線図の変化を調べよ。
ダンパのパラメータを c2 = 1500 および 3500 としたときのゲイン線図の変化を調べよ。
ステップ応答・正弦波応答などをMATLABを利用してシミュレーションせよ。
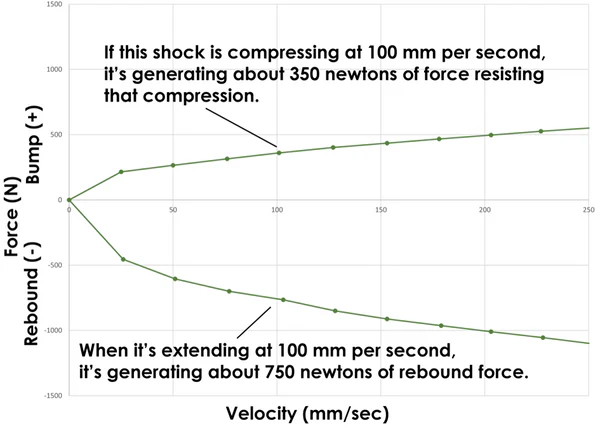
実際のダンパは以下の図のような特性となっている。このダンパの特性を考慮したシミュレーションを実行せよ。

課題6 サンプルプログラム