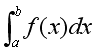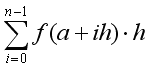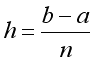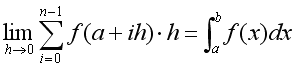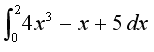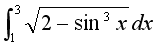第7回　表計算ソフトによる解析

Excelのセル計算を応用すると、ちょっとした科学技術計算を容易に行うことも可能である。今回はその一例として、Excelを利用して数値積分を行ってみる。

本講義で身につけた知識が役立つ科目など：
　機械工学実験，ゼミナール，卒業研究，大学院での研究，企業での報告書作成など。

7.1 数値積分とは

コンピュータの繰り返し機能を利用して、近似的に積分値を求める計算方法である。特に、解析的に積分を行うことが困難である場合に有効である。興味のあるものは、「区分求積法」「数値積分法」「オイラー法」などをキーワードとして調べてみると良い。

7.2 数値積分の理論

図に示すような関数f(x)とx軸で囲まれた部分の面積は、以下の定積分で求められる。

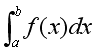
この部分の面積を、下図に示すようなn個の長方形の面積に近似して考える。

この長方形の面積の総和は次式で表される。

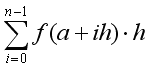
なお、ここで

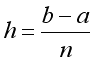
である。nを充分に多くした場合(= hを充分に小さくした場合)、長方形の面積の総和は定積分の値に収束する。すなわち、

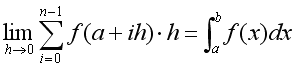
7.3 Excelを利用した数値積分

Excelのセル参照の機能を利用して、繰り返し計算を実現する。例として、以下の関数を被積分関数とした積分計算を行う。

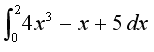
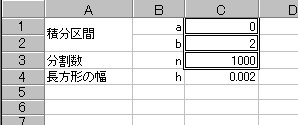
1. まず最初に、積分区間(aおよびb)と分割数(n)より、長方形の幅(h)を計算する部分を作成する。

   

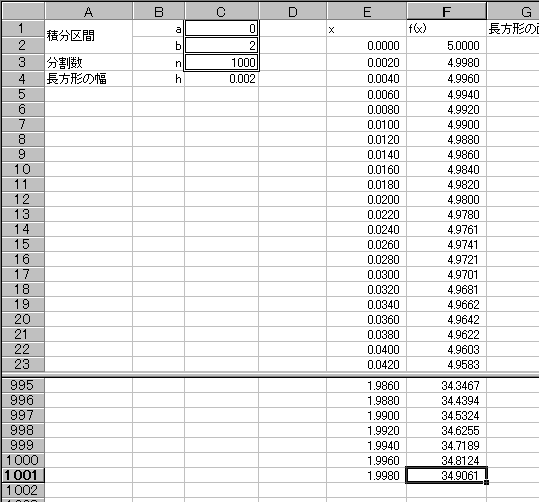
2. 区間aからbのxの値に対し、h刻みでf(x)の値を求める。
   • xの最初の行にはaが入ることになり、その下のセルには (1つ上のセルの値)+h が入ることになる。以降xの値が b-h になるまで同じ計算を繰り返す。
   • f(x)の値は、すぐ左のセルの値(=xの値)を利用して計算を行う。
   • 一箇所だけ計算式を入れれば、後はコピーして貼り付けするだけでよい。
   • べき乗計算は「^」を用いる。(例) 2^4 など。

   

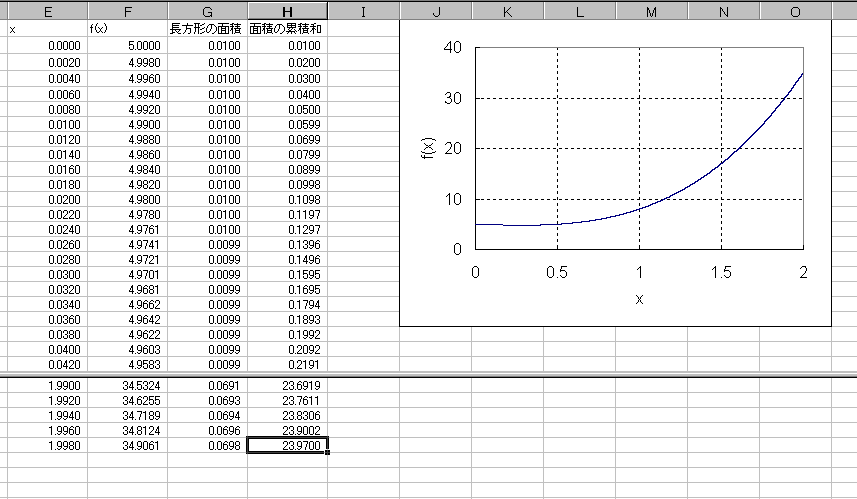
3. xとf(x)の値を利用してグラフを作成する。
4. 微少な長方形のそれぞれの面積(=f(x)*h)を求める。
   • 一番下のxの値は b ではなく b-h となることに注意すること。
5. 面積の累積和を求める。一番下に出てきた値が求める積分値である。

   

6. 分割数を変化させたとき、積分値がどのように変化するか。理論値と比較して誤差がどのようになるかを考察せよ。
   • 遠くのセルへ移動したいときは、「Excelのジャンプ機能(F5キー)」や「Ctrl + カーソル」の機能を利用すると良い。

課題

以下の積分計算を実行せよ。できあがったExcelファイルをOh-o!Meijiシステムにより提出せよ。

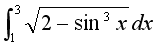
• ヒント：ルートの計算は関数sqrt()を用いる。sqrt(2)など。

提出期限は来週月曜正午までとする。