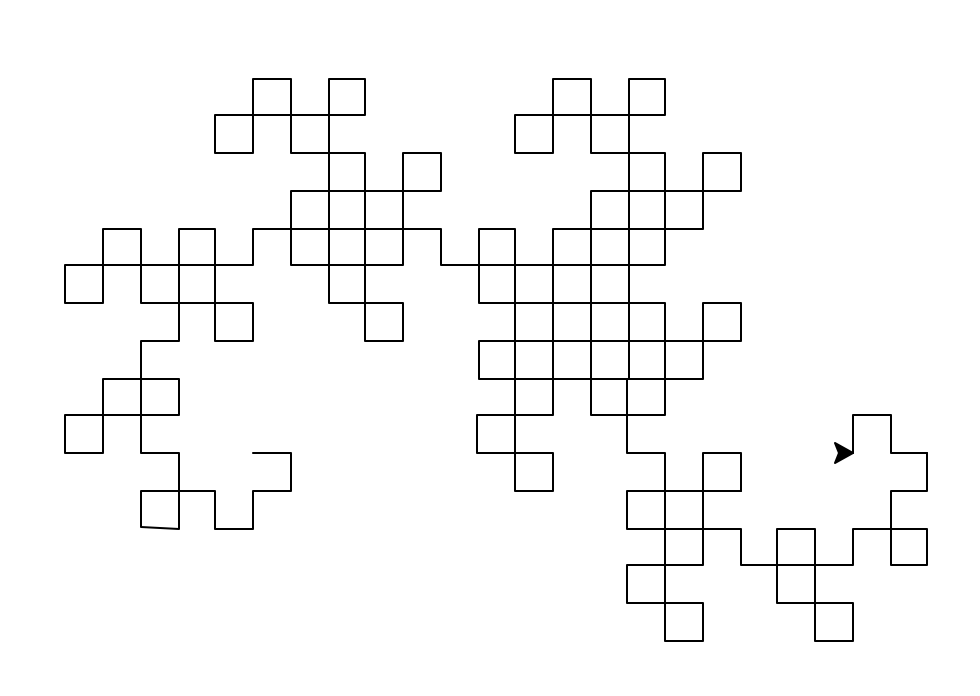亀を再帰的に動かす

Pythonの亀グラフィックスのメソッドで確かめたように、亀グラフィックスでは

• 現在アタマが向いている方向に指定された距離だけ進む
• 現在のアタマの方向から指定された角度だけ左右に向きを変える

それでも、亀は驚くべき軌跡を描き出すことができる。

デフォルトでは、亀は原点で右側（$x$-軸の正の方向）を向いて、ペンダウン pendown（それ以降は亀が移動した軌跡を描く）ダウンの状態で生まれる。 ただし、亀がペンアップ penupしている間は、ふたたびペンダウンするまで亀が移動した軌跡は描かない。

コッホ Koch曲線

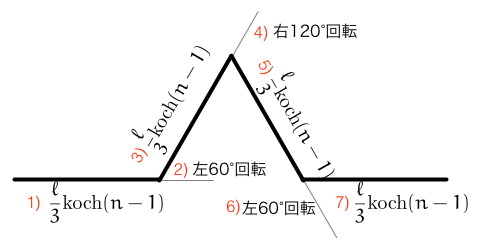
亀 kame が距離 $\ell=$ length を深さ n $(\geqq 0$ だけ turtle_koch(kame, length, n) することを左図のように定義する。

• $n=0$ とき、kame は単に距離 $\ell$ だけ直進する。
• $n>10$ のとき（上図参照）
  1. kame は距離 length/3 を turtle_koch(kame, length/3, n-1) する。
  2. kame の向きを左に 60° 回転する。
  3. kame は距離 length/3 を turtle_koch(kame, length/3, n-1) する。
  4. kame の向きを右に 120° 回転する。
  5. kame は距離 length/3 を turtle_koch(kame, length/3, n-1) する。
  6. kame の向きを左に 60° 回転する。
  7. kame は距離 length/3 を turtle_koch(kame, length/3, n-1) する。

この定義に忠実にPythonで定義したのが、次のスクリプト turtle_koch.py の関数 turtle_koch(kame, length, n) である。

#!/usr/bin/env python
# -*- coding: utf-8 -*-

import turtle

def turtle_koch(kame, length, n):
    if n == 0:
        kame.forward(length)
    else:
        turtle_koch(kame, length / 3, n - 1)
        kame.left(60)
        turtle_koch(kame, length / 3, n - 1)
        kame.right(120)
        turtle_koch(kame, length / 3, n - 1)
        kame.left(60)
        turtle_koch(kame, length / 3, n - 1)

mywin = turtle.Screen()
mykame = turtle.Turtle()

mykame.speed(10) # set maximum speed
mykame.penup() # pen up before movin kame to new position (-300, -200)
mykame.goto(-300, -200)
mykame.pendown() # then pen down. draw trace from now

#k = int(raw_input("k-th curve: k = "))
k= 3 # set depth of interation 
turtle_koch(mykame, 500, k) # try other k

mywin.exitonclick() # keep drawing window until mouse click

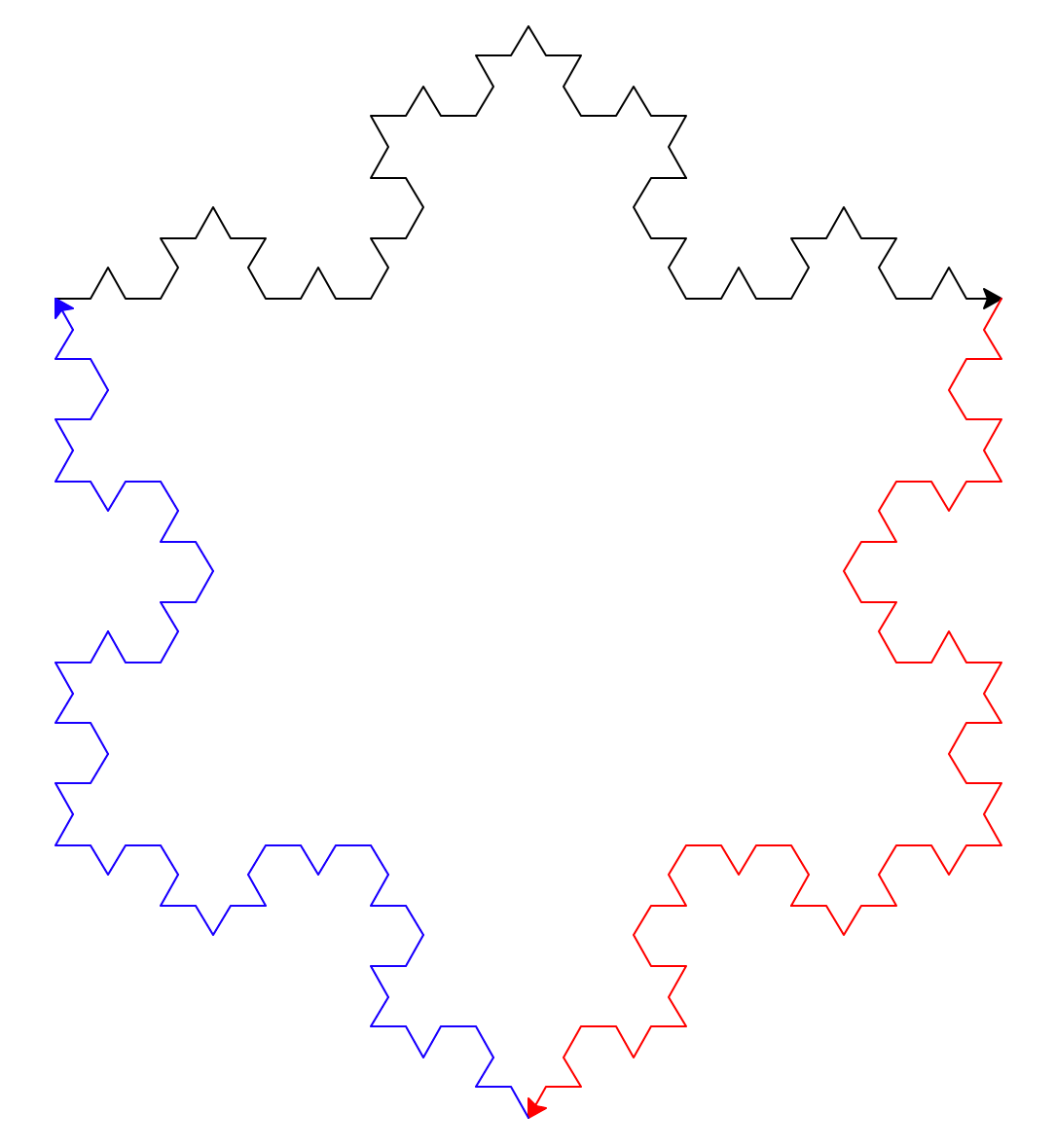演習： 亀三匹 kame1, kame2, kame 3 を使ってKoch曲線をつないで右図（深さ 3。クリックで拡大）のように描くスクリプトを書いて実行しなさい（併せてスクリーンショットも）。
（ヒント）； 亀をスクリーンのどこに設置し､どの位の大きさでKoch曲線を描くかはいろいろ試してみる。 2匹目の亀 kame2 は次のように生成して這わせる（亀のメソッドはを参照）。 一匹目の亀 kame1の頭の最終向き kame1.heading() や最終位置 kame1.position() を使って kame2 を設定することがポイントだ。 色文字列 colorstring には 'black'（デフォルト）以外に、blue', 'red', 'green', 'white', 'yellow', 'violet', 'orange', 'pink' が使える。

kame2 = turtle.Turtle()
kame2.speed(10)
kame2.color('red')
kame2.setheading(kame1.heading())
kame2.right(120)
kame2.penup()
kame2.setposition(kame1.position())
kame2.pendown()
turtle_koch(kame2, 500, k)

レビィ Levy曲線

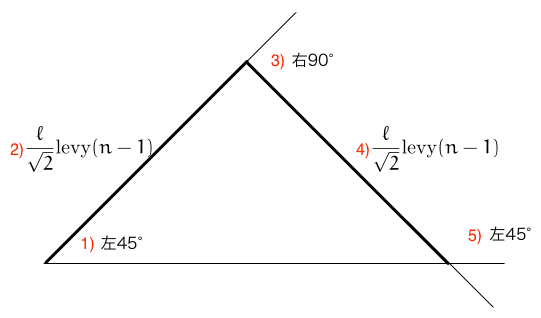
亀 kame が距離 $\ell=$ length を深さ n $(\geqq 0$ だけ turtle_levy(kame, length, n) することを左図（クリックで拡大）のように定義する。

• $n=0$ とき、kame は単に距離 $\ell$ だけ直進する。
• $n>0$ のとき（上図参照）：
  1. kame の向きを左に 45° 回転する。
  2. kame は距離 length/$\sqrt{2}$ を turtle_levy(kame, length/$\sqrt{2}$, n-1) する。
  3. kame の向きを右に 90° 回転する。
  4. kame は距離 length/$\sqrt{2}$ を turtle_levy(kame, length/$\sqrt{2}$, n-1) する。
  5. kame の向きを左に 45° 回転する。

この定義に忠実にPythonで定義したのが、次のスクリプト turtle_levy.py の関数 levy_curve(kame, length, n) である。

#!/usr/bin/env python
# -*- coding: utf-8 -*-

import turtle
import math

def levy_curve(kame, length, depth):
    if depth == 0:
        kame.forward(length)
    else:
        kame.left(45)
        levy_curve(kame, length/math.sqrt(2), depth - 1)
        kame.right(90)
        levy_curve(kame, length/math.sqrt(2), depth - 1)
        kame.left(45)


mywin =  turtle.Screen()
mykame = turtle.Turtle()
mykame.speed(10)
levy_curve(mykame, 300, 4)

mywin.exitonclick()

Sierpiński gasket シェルピンスキー・ガスケット

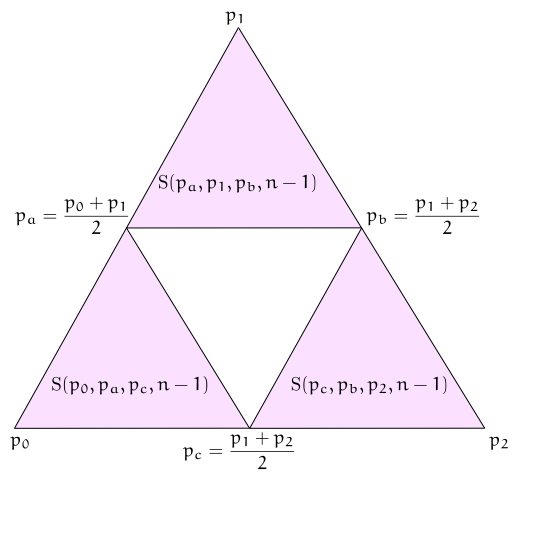
三角形（正三角形が原義である）をなす3点 $p_0$, $p_1$, $p_2$ における深さ $n$ の Sierpiński ガスケット $\mathrm{S}(p_0,p_1,p_2,n)$ は、左図（クリックで拡大）のように、3つの深さ $n-1$ のSierpińskiガスケット $\mathrm{S}(p_0,p_a,p_c,n-1)$, $\mathrm{S}(p_a,p_1,p_b,n-1)$ および $\mathrm{S}(p_c,p_b,p_2,n-1)$ からなると定義する。

ここで、点 $p_a$ は $p_0$ と $p_1$ の中点、点 $p_b$ は $p_1$ と $p_2$ の中点、点 $p_c$ は $p_0$ と $p_2$ の中点である。 具体的には、たとえば $p_a=(p_{ax},p_{ay})$ は \[ p_a=(p_{ax},p_{ay})=\frac{p_0+p_1}{2}=\left(\frac{p_{0x}+p_{1x}}{2}, \frac{p_{0y}+p_{1y}}{2}\right) \] である。

すなわち Sierpiński ガスケット $\mathrm{S}(p_0,p_1,p_2,n)$ は次の関係を満たす。 \[ \mathrm{S}(p_0,p_1,p_2,n) = \mathrm{S}(p_0,p_a,p_c,n-1) \cup \mathrm{S}(p_a,p_1,p_b,n-1)\cup \mathrm{S}(p_c,p_b,p_2,n-1) \] であって、真ん中の三角形 $\triangle p_a p_bp_c$ 領域は抜け落ちていることに注意する。

亀でSierpińskiガスケットを描かせる

以下に、与えられた3点からなるリスト point を使って、亀 kame が右図（クリックで拡大）のような Sierpińskiガスケット（深さ 4）を描く関数 turtle_sierpinski(kame, points, depth) を考えよう。 幾何学的には、上の図を描けばよいので、手で描くには簡単だ。 深さによって描く三角形に色を付けるところに亀の工夫がある。

亀 kame に3角形を描かせる

そのために、まず、与えられた3点からなるリスト point を使って亀 kame が3角形を描く関数 draw_triangle(kame, points, color) を定義する。 draw_triangle(kame, points, color) は、亀 kame が3点からなるリスト point を使って 色 color で塗りつぶした三角形を描く関数である。 リスト point は [point[0], point[1], point[2]] としており、さらに各点 point[i] は $x$, $y$-成分を持つリスト [point[i][0], point[i][1]] からなっている。

def draw_triangle(kame, points, color):
    # draw fill-color triangle on clockwise points
    kame.fillcolor(color) # set fill-color
    kame.up() # penup during moving
    kame.goto(points[0][0],points[0][1])
    kame.down() # pendown after positionig
    kame.begin_fill() # set fill-mode
    kame.goto(points[1][0], points[1][1])  # strat point of polygon
    kame.goto(points[2][0], points[2][1])
    kame.goto(points[0][0], points[0][1])  # final point of polygon(3 points in thi scase)
    kame.end_fill() # paint with fill color

ここで、draw_triangle に渡している3角形を描くための3点からリスト points は、上のスクリプトからわかるように、二重のリストになっていて次の構造になっている（実際のスクリプトが上手く動くためには、こうしたデータの整合性について細心の配慮が必要だ）。

points = [points[0], points[1], points[2]]
       = [ [points[0][0], points[0][1]], [points[1][0], points[1][1]], [points[2][0], points[2][1]] ]

点の中点を求める

2点 p1, p2 を与えてその中点の座標を返す関数 get_midpoint(p1, p2) は次のようになる。 ここでも同様に、渡される p1 と p2 については平面上の点として扱えるように構成されていなければならない。

def get_midpoint(p1, p2):
    return ((p1[0] + p2[0]) / 2, (p1[1] + p2[1]) / 2)

Sierpińskiガスケットを描く

以上の準備、与えられた3点からなるリスト point を使って亀 kame が3角形を描くための関数 draw_triangle(kame, points, color) 、、与えられた1二点 p1 と p2 の中点の座標を返す関数 get_midpoint(p1, p2) を使うと、亀 kame 深さ n のSierpińskiガスケットを描く関数 turtle_sierpinski(kame, points, depth) を次のように描くことができる。

深さ n に応じて三角形を描くための色を7成分からなる文字列リスト bgcolor = ['blue', 'red', 'green', 'white', 'yellow', 'violet', 'orange'] から選び出すために、正数商 n % n を使っている。

def turtle_sierpinski(kame, points, depth):
    bgcolor = ['blue', 'red', 'green', 'white', 'yellow',
            'violet', 'orange']
    draw_triangle(kame, points, bgcolor[depth % 7])
    if depth > 0:
        turtle_sierpinski(kame, [points[0], get_midpoint(points[0], points[1]),
                  get_midpoint(points[0], points[2])], depth - 1)
        turtle_sierpinski(kame, [points[1], get_midpoint(points[0], points[1]),
                  get_midpoint(points[1], points[2])], depth - 1)
        turtle_sierpinski(kame, [points[2], get_midpoint(points[2], points[1]),
                  get_midpoint(points[0], points[2])], depth - 1)

mywin =  turtle.Screen()

mykame = turtle.Turtle()
mykame.speed(10)

mypoints = [[-200, -100], [0, 246], [200, -100]] # この3点の座標は概ね正三角形に近い
turtle_sierpinski(mykame, mypoints, 4)

mywin.exitonclick()

ドラゴン dragon曲線

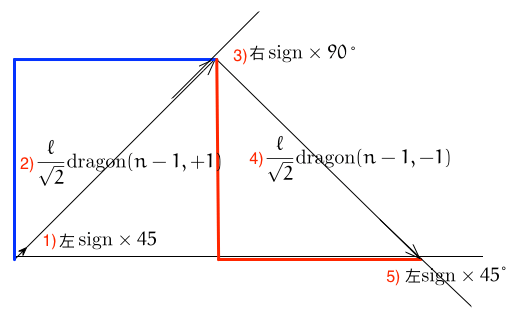
Levy曲線は直線を、それを底辺とする直角二等辺三角形の直交する2辺で置き換えていくものであった。 その置き換えは、直線の進行方向に対して二辺を常に外側に置き換えている。

左図（クリックして拡大）のように、「二等辺三角形の2辺に関して交互に」進行方向について外側と内側に置き換えを繰り返して定義してみるとどうなるだろうか。

亀 kame が距離 $\ell=$ length を深さ n $(\geqq 0)$ だけ turtle_dragon(kame, length, n, sign) することを次のように定義する（sign = $\pm 1$ ）。

• $n=0$ ときには、kame は単に距離 $\ell$ だけ直進する。
• $n>0$ のときは、kame は次のように這う（上図参照）。
  1. kame の向きを左に sign $\times$ 45° 回転する。
  2. kame は距離 length/$\sqrt{2}$ を turtle_dragon(kame, length/$\sqrt{2}$, n-1, 1) する。
  3. kame の向きを右に sign $\times $ 90° 回転する。
  4. kame は距離 length/$\sqrt{2}$ を turtle_levy(kame, length/$\sqrt{2}$, n-1, -1) する。
  5. kame の向きを左に sign $\times $ 45° 回転する。

演習： 右図は深さ 3 のdragon曲線である。 これを描くスクリプト turtle_dragon.py を描いて実行しなさい。 併せて、スクリーンショットも撮りなさい。

dragin曲線は、紙折り曲線（paper folding curves）の仲間として重要で、多くの深い研究がある。 細長く紙を切り出して、半分の長さになるように同じ方向（紙の右端が左端に時計回りに（あるいは反時計回りに）半分に折り畳む操作を繰り返して続ける（一階の操作で紙の長さは $\frac12$ になる）。 $n=0,1,2,3,\dots$ と折り畳み操作を行ってから、その折れ目が直角（90°）になるようにして、紙を開いてみよ。そのときの曲線が turtle_dragon(kame, length, n, +1) または turtle_dragon(kame, length, n, -1) である。

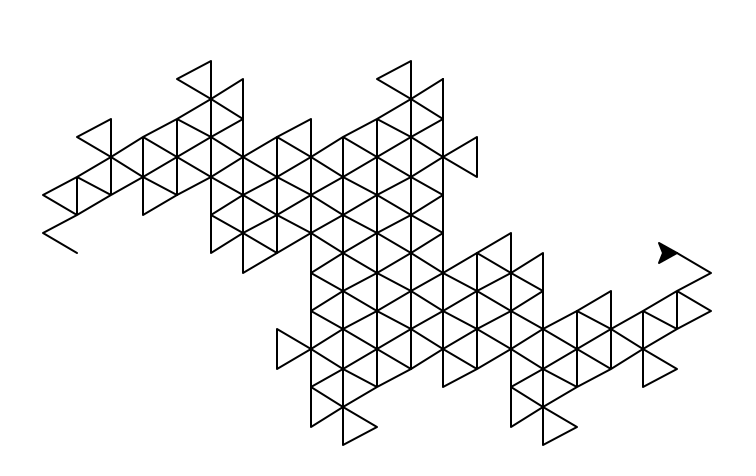演習： 次の関数 tetradragon_curve(kame, length, depth) を使って、カメに軌跡を描かせなさい。 この軌跡と紙折り曲線との関連について、考えなさい。

def tetradragon_curve(kame, length, depth):
    if depth == 0:
        kame.forward(length)
    else:
        kame.left(30)
        tetradragon_curve(kame, length/math.sqrt(3), depth - 1)
        kame.right(120)
        tetradragon_curve(kame, length/math.sqrt(3), depth - 1)
        kame.left(120)
        tetradragon_curve(kame, length/math.sqrt(3), depth - 1)
        kame.right(30)

亀は植物を模倣する

形態学立場での植物（plan）の定義とは何だろうか。 その一つとして、木構造（tree structure）が挙げられる。 根（root）から枝分かれを繰り返して、葉（leaf）に至るという構造で、葉までの道筋は一意で閉路（closed path）を持たない。
『The Algorithmic Beauty of Plants』（Przemyslaw Prusinkiewicz and Aristid Lindenmayer, Springer 1991）は､記号言語理論と人工植物生成を関係づけ追求した腐朽の書だ。

次の亀はどのような軌跡を生み出すかを予測することができるだろうか？。 カメの後ずさりメソッド backward を使っている。 このスクリプト turtle_plant.py も深く考えるに値する。

#!/usr/bin/env python
# -*- coding: utf-8 -*-

import turtle
#my_turtle = turtle.Turtle()
#my_win = turtle.Screen()

def tree_like_plant(kame, branch_len):
    if branch_len > 5:
        kame.forward(branch_len)
        kame.right(30)
        tree_like_plant(kame, branch_len - 20)
        kame.left(50)
        tree_like_plant(kame, branch_len - 10)
        kame.right(20) # attention! 50 = 30 + 20
        kame.backward(branch_len)

mywin = turtle.Screen()
mykame = turtle.Turtle()
mykame.speed(10)
mykame.color("green")
mykame.penup()
mykame.left(90) # set kame diretion basically to upward
mykame.goto(0, -200)
mykame.pendown()

tree_like_plant(mykame, 100)

mywin.exitonclick()

---

Copyright 2004 水谷正大