Webページでは数式を表すためにLaTeX表記が使えるMathJaxを利用しています。 WebブラウザにはSafari/Chrome/Firefoxを使って下さい（IEでは表示できないようです。）

再帰再訪--計算時間

Fibonacci数列

Fibonacci数列 $\{ f(n)\}_{n=0,1,2,\dots}$ はよく知られている数列宇で次で定義される。 $n$番目のFibonacci数を $fib(n)$ と書くと次のような漸化式が成立する。

\begin{align*} fib(0) & = 1,\\ fib(1) &= 1,\\ fib(n) & = fib(n-1) + fib(n-2), \quad n \geqq 2. \end{align*}

次のスクリプト fibonacci.py では、関数 fibonacci_recur(n) では$n$番目のFibonacci数を返す関数を再帰的に定義し、キーボードから非負整数文字列を整数 n として fibonacci(n) を計算するに要する時間[sec]と併せてFibonacci値をプリントしている。

#!/usr/bin/env python
# -*- coding: utf-8 -*-

import time

def fibonacci_recur(n):
    if n == 0:
        return 1
    elif n == 1:
        return 1
    else:
        return fibonacci_recur(n - 1) + fibonacci_recur(n - 2)

n = int(raw_input("Calculating n-th Fibonacci numbers:  n(> 0) = "))
start_time = time.time()
fib = fibonacci_recur(n)
end_time = time.time()
print "Recursive version: used time = :", end_time - start_time
print "\tFibonacci number = ", fib

演習：上のスクリプトfibonacci.pyを実行しなさい。さらに、$n$番目のFibonacci数を返す関数としてfor文を使って定義する関数 fibonacci_for(n) を併せて書いて、実行結果を次のようになるように書き直しなさい。

$ ./fibonacci.py
Calculating n-th Fibonacci number:  n(> 0) = 20
For version: used time = : 4.57763671875e-05 [sec]
	Fibonacci number =  10946
Recursive version: used time = : 0.0022919178009 [sec]
	Fibonacci number =  10946

関数引数

Pythonでは関数名を関数の引数として渡して処理することが可能である。これを関数引数という。

たとえば、つぎのようなスクリプトが可能である。関数 used_time を2つの仮引数 procedure と n を渡すようにして定義する。 timeモジュールをインポートしているので、procedure(n) の実行を測定し、その経過時間 end_time - start_time を返すというのが関数 used_time(procedure, n) の働きである。つまり、used_time(procedure, n) は関数 procedure が procedure(n) に要する処理時間を返す関数である。

import time

def used_time(procedure, n):
    start_time = time.time()
    result = procedure(n)
    end_time = time.time()
    return end_time - start_time

この関数 used_time(procedure, n) を使えば、2つの関数 fibonacci_for と fibonacci_recur が 1番目から n番目(n> 1)のFibonacci数を計算するに要する時間を次のように並べて書き出すことができる。この n はキーボードから入力した正整数文字列から与えている。

n = int(raw_input("Calculating n-th Fibonacci number:  n(> 0) = "))
for i in range(1, n + 1):
    print i, used_time(fibonacci_for, i), '\t',used_time(fibonacci_recur, i)

次の実行結果は、キーボードから正整数 n を与えて、1番目からn番目までのFibonacci数に関して、2つの関数 fibonacci_for と fibonacci_recur を使って i 番目の値を計算するために必要な時間を並べて出力するスクリプト calc_time_fibonacci.py の実行結果である。

./calc_time_fibonacci.py
Calculating n-th Fibonacci number:  n(> 0) = 30
1 3.09944152832e-06 	9.53674316406e-07
2 2.14576721191e-06 	1.19209289551e-06
...........
...........
24 1.50203704834e-05 	0.0149919986725
25 7.86781311035e-06 	0.0260441303253
26 8.10623168945e-06 	0.040717124939
27 8.10623168945e-06 	0.0683250427246
28 9.05990600586e-06 	0.104562997818
29 8.10623168945e-06 	0.16804599762
30 8.10623168945e-06 	0.269570112228

演習： calc_time_fibonacci.py を書いて、実際に実行してみなさい（n = 10 当たりから入力していくのが無難だ）。入力する n を大きくしていくと何が観察されるだろうか。

次は、calc_time_fibonacci.py を修正して、laptime_fibonacci.csv を書き込みモードで開いて、2津の関すの実行時間をカンマ(,)区切りで、最後に改行 '\n' を加えて書き出すようにした。つまり、1行のデータ要素がカンマ(,)で区切られている（このような形式をファイルをcsv（comma separated value）ファイルという。 Excelなどの表計算で加工処理できる）。 fh.write( ) は文字列として書き出すように数値を str を使って文字列に変更している。

fh = open('laptime_fibonacci.csv','w')

n = int(raw_input("Calculating n-th Fibonacci numbers:  n(> 0) = "))
for i in range(1, n + 1):
    # print i, used_time(fibonacci_for, i), '\t',used_time(fibonacci_recur, i)
    fh.write(str(used_time(fibonacci_for, i)) + ','+ str(used_time(fibonacci_recur, i))+'\n')

fh.close()

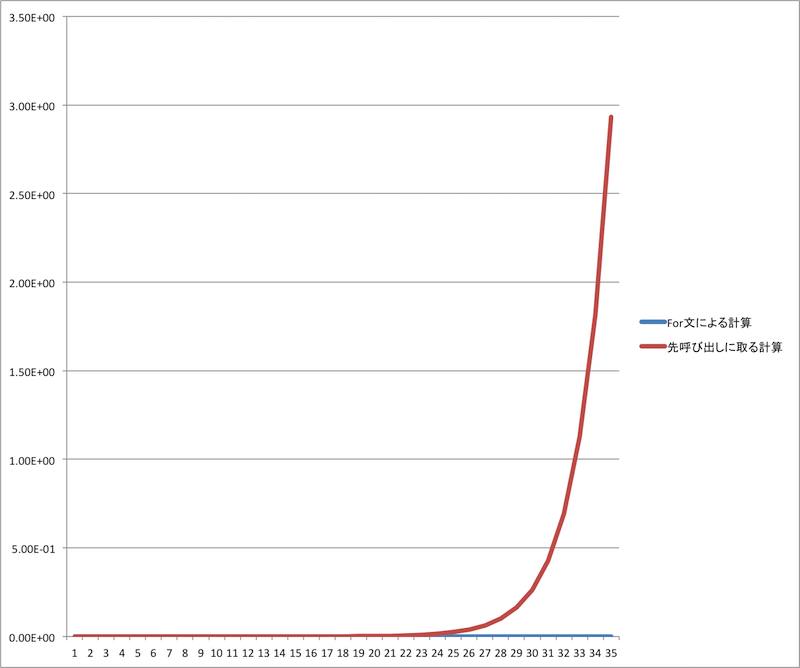
再帰を使わずにfor文でFibonacci数を計算した計算時間（青色）に比べて、再帰的定義を使って計算した計算時間（赤色）は $n$ はが増えると急速に増加していることがわかる。

演習：リスト要素の和と計算時間の測定において、for文を使った関数 sum_lis と再帰的に定義した関数 sum_list_recur を使って、ロストの長さを $n$ としたとき、同様にして2つの計算時間を比較するスクリプトを書いて、その結果を csvファイルに書き出して、グラフ化してみなさい。

ベクトルの$L_1$ノルム

$n$個の成分を持つベクトル $v=(v_0, v_1, \dots, v_{n-1})$の$L_1$のノルム $\Vert v\Vert_1$ は次のようである。

\[ \Vert v\Vert_1 =|v_0| + |v_1| +\dots + |v_{n-1}|. \]

Pythonではベクトル$v$をリスト num_list = [$v_0$, $v_1$, $\dots$, $v_{n-1}$] で表すことができ、その$L_1$ノルムを返す関数 one_norm_recur[num_list] を考えよう。数値リスト num_list は空でなく1以上の要素を持つと仮定する。

リスト num_list が2つ以上の要素（長さ2以上）を持つ場合、リストの先頭（0番目）から末尾（len(num_list -1 番目）における中間位置を mid = int(math.floor(len(num_list) / 2)) で求めておくと、リスト前半のリストは num_list[: mid] 、リスト後半のリストは num_list[mid: ] である。浮動小数 x の x を越えない最大の整数（数学ではGauss記号 $[x]$で表記）返すFloor関数 math.floor() を使うために math モジュールをインポートしている。

したがって、ベクトル num_list が長さ2以上のリストであるとき、$L_1$ノルム one_norm_recur[num_list] は、上の定義よりそれぞれの部分リストの$L_1$ノルムの和 one_norm_recur(num_list[: mid]) + one_norm_recur(num_list[mid: ]) である。この事実を使って、 $L_1$ノルムを返す関数 one_norm_recur[num_list] は次のように再帰的に定義できる。

import math

def one_norm_recur(num_list):
    if len(num_list) == 1:
        return math.fabs(num_list[0])
    else:
        mid = int(math.floor(len(num_list) / 2))
        return one_norm_recur(num_list[: mid]) + one_norm_recur(num_list[mid: ])

演習： 1つ以上の要素を持つリスト（ベクトル）num_list の$L_1$ノルムを計算する関数再帰的定義 one_norm_recur[num_list] に加えて、繰り返し文 for を使った関数 one_norm_for[num_list] を定義しなさい。

正整数 $n$ をキーボードから入力して、0.0 から 1.0 までの乱数を使って $1\leqq i\leqq n$個からなるリストを生成し、その$L_1$ノルムを求めるに要した計算時間を2つ1行に書き出すスクリプト one_norm.py を書きなさい。次はその実行結果の一部である。

$ ./one_norm.py
Calculating 1 norms of random vectors with n (> 0) elements = 200
1.00135803223e-05 	2.69412994385e-05
2.86102294922e-06 	1.8835067749e-05
3.09944152832e-06 	1.28746032715e-05
3.09944152832e-06 	1.4066696167e-05
........
........
2.31266021729e-05 	0.000375032424927
2.28881835938e-05 	0.000353097915649
3.48091125488e-05 	0.000358819961548
1.59740447998e-05 	0.000349998474121

さらにこの結果を各行のデータがカンマ(,)区切りであるようにファイル laptime_one_norm.csv に書き出すように修正して､その様子をグラフに表示してみなさい。