タートルグラフィックス
Mathematicaパッケージの使い方として、タートルグラフィックスを取り上げよう。
筆者で作成したタートルグラフィックスのためのMathematicaパッケージ Turtle.zipを展開し Turtle.m をMathematica内で次のコマンドで返るフォルダ場所(なければ作成する)に置く。
FileNameJoin[{$UserBaseDirectory, "Applications"}]
MacOSなら次のようになる:"/Users/username/Library/Mathematica/Applications"
Mathematicaからパッケージ Turtle.m を読み込むには、Mathematica Notebook の冒頭で次のように書いて実行する(記号 (`) はバッククォート backquote である)。
<< Turtle`
このMathematicaパッケージで利用できる関数は次のようである。必要なら Turtle.m に関数を追加すればよい。
| initializeTurtle[start] | 引数リストstart({x,y})で指定した位置に亀をセット。引数省力時には {0,0} をデフォルトに。 |
|---|---|
| setTurtleDirection[angle] | 亀の向きを angle(radian) にセット。省略時は 0 |
| rightTurn[a] | 現在の亀の向きを右に a(radian)回転 |
| leftTurn[a] | 現在の亀の向きを左に a(radian)回転 |
| forwardTurtle[s] | 現在の亀の方向に s だけ前進 |
| backwardTurtle[s] | 現在の亀の方向に s だけ後退 |
| showTurtlePath | 亀の軌跡を線で描く(引数なし)。位置のリストをLineでつなぐ) |
| getTurtlePath | 亀の位置リストを返す(引数なし) |
| getTurtlePosition | 亀の現在位置を返す(引数なし) |
| getTurtleDirection | 亀の現在方向(radian)を返す(引数なし) |
Koch曲線を描く
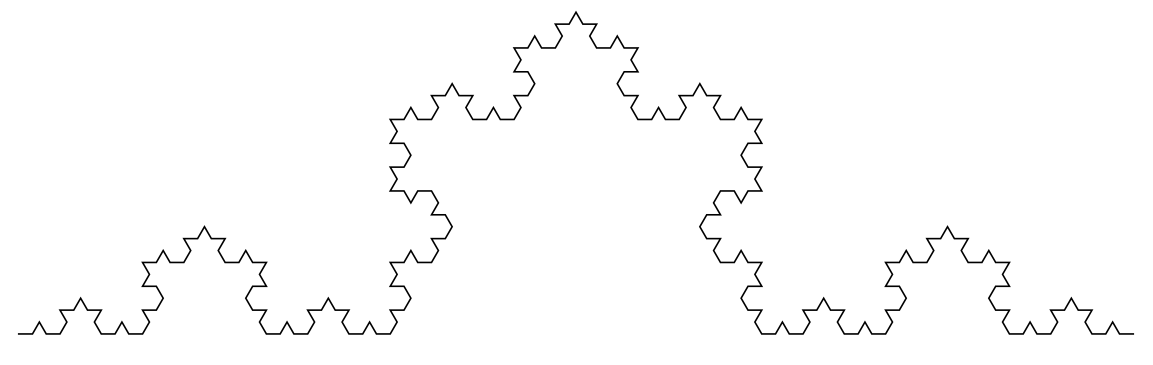
右図は以下のMathematicaコードで描いたタートルグラフィックによるKoch曲線である。
(* パッケージ Turtle の読み込み *)
<< Turtle`
(* Koch曲線のTurtle的定義: length 両端の距離、Koch曲線のフラクタル的深さ *)
kochCurve[length_, 0] := forwardTurtle[length];
kochCurve[length_, depth_] := Module[{},
kochCurve[length/3, depth - 1];
leftTurn[Pi/3];
kochCurve[length/3, depth - 1];
rightTurn[2 Pi/3];
kochCurve[length/3, depth - 1];
leftTurn[Pi/3];
kochCurve[length/3, depth - 1]
]
(* Koch curveを描く手順 *)
initializeTurtle[]; (* 亀の初期化 *)
kochCurve[1, 4]; (* 長さ1 深さ4のKochポイントを求める *)
getTurtlePath[] (* 必要ならKochポイントのリストを表示 *)
showTurtlePath (* Koch曲線を描く *)
(* Koch Curve を描く関数 *)
showKochCurve[n_] := Module[{},
initializeTurtle[];
kochCurve[1, n];
showTurtlePath
]
showKochCurve[3]
Paper folding曲線(dragon曲線)を描く
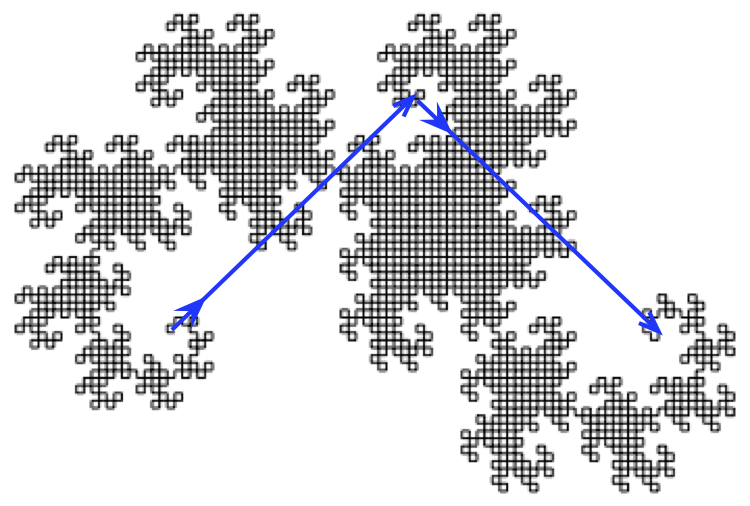
右図のPaperfolding曲線(Dragon曲線)をタートルグラフィックスで描いてみよう。 foldingの仕方から明らかであるが、右図で$\frac{\pi}{2}$で交わる骨格部を表す2部分は前回のfoldingで得られた曲線が真ん中でつながっている。 この意味でPaperfolding曲線は自己相似形である。
再帰的亀で描く
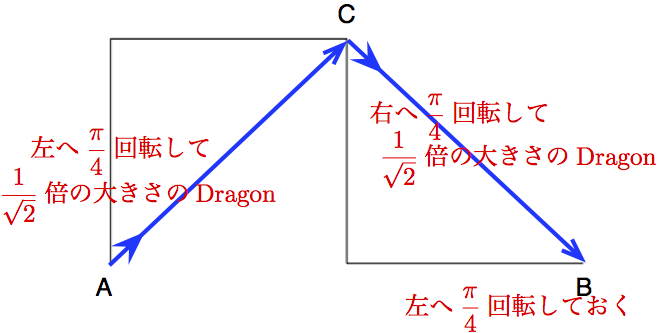
Paperfolding曲線の成り立ちを観察するとわかるように、 $n$回折れたたんだPaperfoloding曲線の折れ曲がり角点列を両端点間を長さ length 間で得る paperfolding_dragon[length, n] を考えてみよう()。
左図のようにして直線をそれを底辺とする直角三角形をなす2本の直線で再帰的に置き換えていく。 このとき、置き換える直角三角形(の辺)が直線の進行方向に左右交互に45度回転するように工夫することがポイントである。 そのために、折り畳み点列を返す関数として paperFoldingDragon[length, depth, parity] のように1,-1を取るparity変数を引数に加えて定義すればよい。 最後に、「左に parity $\cdot \frac{\pi}{4}$ 回転しておく」も必要なことも理解しよう(この操作をしないとどうなるかを試してみよう)。
paperFoldingDragon[length_, 0, parity_] := forwardTurtle[length];
paperFoldingDragon[length_, depth_, parity_] := Module[{},
leftTurn[parity Pi/4];
paperFoldingDragon[length/Sqrt[2], depth - 1, 1];
rightTurn[parity Pi/2];
paperFoldingDragon[length/Sqrt[2], depth - 1, -1];
leftTurn[parity Pi/4];
]
showPaperFoldingDragon[depth_] := Module[{},
initializeTurtle[];
paperFoldingDragon[1, depth, 1];
showTurtlePath
]
紙折り列にしたがって歩く亀で描く
紙折り列と紙折り曲線にあるように、紙を2つ折り操作を $n$ 回繰り返して得られる記号 d と u からなる2-folding列を求めておく(記号 d と u の亀の向き変化は、上の図に合わせるために逆になる)。
初期化 initializeTurtle[] された亀の方向は 0度方向を向いている。 原点{0,0}から位置{1,0}まで forwardTurtle[1.0] で歩いた亀は、2-folding列 foldstring を読みながら次のように向きを変える。
- 記号 d に出会うと、向きを右に90度回転 rightTurn[Pi/2]
- 記号 u に出会うと、向きを左に90度回転 leftTurn[Pi/2]
kame.forward(1.0)
for i in range(0, len(foldstring)):
if foldstring[i] == 'd':
kame.right(Pi/2)
elif foldstring[i] == 'u':
kame.left(Pi/2)
kame.forward(1.0)
