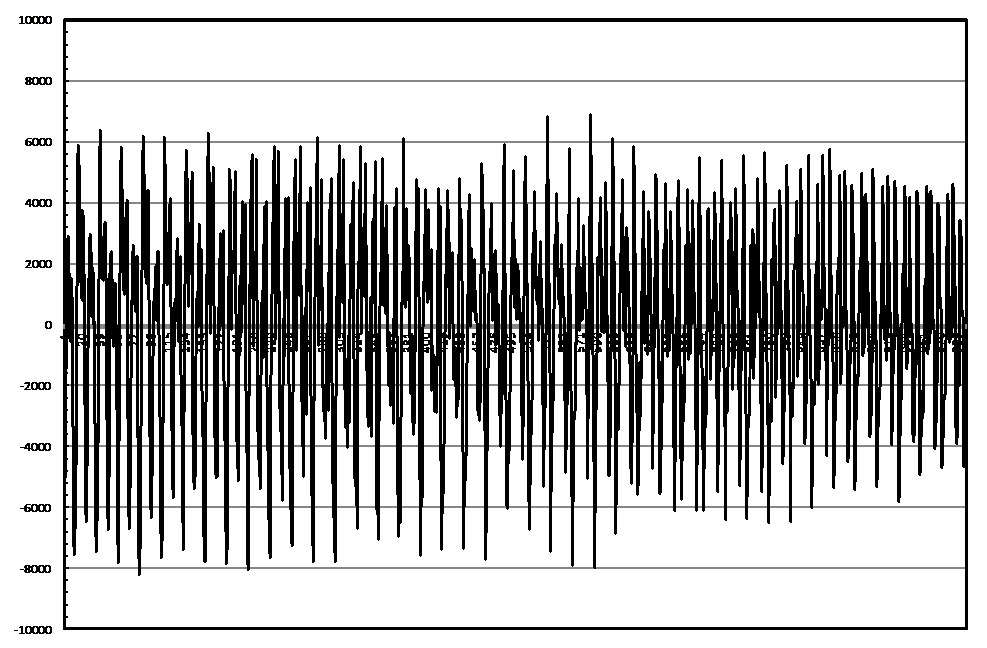
図1.wave.txt内の波形データの表示例.
今回は,前回までの演習で準備した関数群を使って,実際のDFT処理を行う.
さて,フーリエ変換に関する用語を,以下のようにまとめておく.
| 対象とする信号の長さ | 扱う周波数 | 特徴 | |
| フーリエ変換 | 無限に続く連続信号 | 無限の周波数のcos, sinの重ね合わせで表現 | 任意の信号に適用できるが,コンピュータでは連続関数は扱えない |
| 離散フーリエ変換(DFT):今日の演習 | 有限長のN 個の離散信号 | 有限のN 個の周波数のcos, sinの和で表現 | ある有限長の信号を離散化し,その刻みに相当する周波数まで分解できる.ある時間長の信号が永遠に繰り返される前提 |
| 高速(離散)フーリエ変換(FFT) | 同上 | 同上 | データ数が小さな素数の累乗で表される時,計算量が劇的に少なくなる |
実際のスペクトル解析には FFT(高速フーリエ変換)が広く用いられているが,フーリエ変換の原理を知るにはまず DFT について学ぶ方が良い.(DFTとFFTの計算結果は一致する.)
DFT と FFTの違いは,計算量(つまり計算時間)にあり,計算結果は基本的に全く同じになる.
DFT の計算時間はN2に比例するのに対し,FFTは N log2(N/2)の計算時間しかかからないので,特にデータ数Nが大きくなるほど,FFTによる時間短縮の効果は大きくなる.
今回の提出物は,通常のソースファイル(.cpp,.h)に加えてExcelなどのグラフ(.xls or .xlsx形式)も提出すること.
本ページ末尾を参考にDFT演算を行うプログラムを作成し,
sin_waves(), square_wave() 関数で得られる波形のパワースペクトル(DFTを行った後,得られた複素数配列の各要素の絶対値の2乗)を計算せよ.
計算結果は fopen(), fprintf() 関数などを用いて csv ファイルに出力し,下方の例に倣ってパワースペクトルを書け.
main() 関数から,上記波形生成関数を呼び出して,配列にデータを入力する.波形データファイル wave.txtには,ある1000個の整数型の楽器の演奏データが格納されている.
まずこのファイルを右クリック,名前をつけて保存せよ.
次に,

図1.wave.txt内の波形データの表示例.
パワースペクトルは,下の図のような感じになるはずである.
横軸は波数,縦軸はパワー(絶対値の2乗)の対数表示である.
(このようなグラフを片対数グラフという.)

図2.wave.txt の波形を(離散)フーリエ変換し,得られたパワースペクトル.
横軸は波数(元のデータ区間内に何個の波が入るか),縦軸はその波数の振幅の二乗(の相対値).
ファイルのデータを保存する場合,fopen(),fprintf(),fclose()などのファイル操作関数を使うのが定石だが,もっと手軽に画面出力をファイルに保存場合のテクニックを紹介する.
実行ファイルの入力に続けて,>記号とファイル名を下記のように書く.
153R000000-00-1.exe > file.csv
この操作により,本来画面に出力されるものがファイルへと書き出される.
計算・処理手順をよく理解すること.
void dft(const double in[], Complex out[], const int N)
//
// 離散フーリエ変換(DFT)
// 元データは実数,変換後は複素数
//
// in : 元データ.これは変更しない.実数の配列.
// out : 計算結果.こちらは複素数.
// N : データ個数.inもoutも同じデータ数でなければならない
//
{
int t;
/* 出力用の配列を初期化 */
for(t=0; t<N; t++) {
out[t].re = 0.0;
out[t].im = 0.0;
}
for(int f=0; f<N; f++) {
// 以下のループで 1個のF[omega]を計算する.
double omega = 2 * pi * f;
for(t=0; t<N; t++) {
/* 積分の中身の計算 */
out[f] = Cadd(out[f], Cmul( ToComplex(in[t], 0.0), Cexp( ToComplex(0.0, -omega * t/N) )));
}
}
}
フーリエ変換を行うための基本は,バタフライ演算という演算で,離散的波形データにおいて,あるデータの前後何点かと加減算を繰り返しながら周波数ごとのレベルを算出してゆく..
細かいアルゴリズムは多様であり,例えば以下の表のようなものが挙げられる.
離散量を対象としているため,あるまとまったデータ数を用いて処理を行う.
FFTのアルゴリズムの計算上,基数というキーワードがあり,基数のべき乗のデータ数の処理を行う際に計算を高速化できる.
例えば,基数2なら N = 1024(2の10乗)とか 2048, 4096 のデータをひとまとめとして計算する.
基数4であれば,N=1024, 4096, 16384個となる.
| 基数 | FFTの型 | ビット逆転演算 | 計算時間比 | |
| 2 | 2進展開型 | 計算時に配列に入る | 1.000 | 基本となる基数2のFFT |
| 2 | 2進展開型 | 利用する | 0.995 | 上記方法からビット列逆転演算を分け,配列を 直接操作せず,別途カウンタの変数を利用する |
| 2 | 時間間引き型 | 必要 | 0.946 | Cooley-Tukeyの方法と呼ばれる データNを基数と偶数に分けて演算 |
| 2 | 非インプレイス型 | 不要 | 1.142 | 上記のアルゴリズムの派生形 データや結果のビット列を逆順にする必要がない 本来は時間のかかる処理を省略できる方法だが 計算結果が速くなるわけでもない (上記は逆順にした結果を次の演算で利用できる ためそれほど時間ロスがあるわけでもないため) |
| 2 | 周波数間引き型 | 必要 | 0.998 | Sandle-Tukeyの方法と呼ばれる 偶数個データNを前半と後半に分けて演算 |
| 4 | 4進展開型 | 不要 | 0.897 | 加減算だけで計算できる 原理上は基数2の3/4の時間で演算可能 |
| 2 | N/2データ 2組実数データ |
他のFFTと組み合わせ | 0.665 |