第7回　フーリエ変換(1)

今週の実習では，フーリエ変換のプログラミングの準備として，波形生成などいくつかの関数を用意する．

課題1

FFTによる解析のため，以下に挙げる関数を準備せよ．
ヘッダファイルおよび実装ファイル名はそれぞれ 153R000000-07-dft.h , 153R000000-07-dft.cpp とする．
main関数を含むファイルは153R000000-07-1.cpp とする.
（000000の部分は学生番号）

各関数は，main関数から呼び出し，正しく動作するか確認すること．
後半のダミーの波形データ生成関数については，得られた波形の形状をグラフにして確認すること． グラフの提出は不要．
（画面に出力したものExcelに貼り付けるか，ファイルにcsv形式で出力しExcelで描画．）
以下，特に指定が無い限り x は信号データの格納された実数型配列， n は配列の要素数（データ個数） である．
どんな n が渡されてきても，うまく動く関数を作ろう．
n=100程度で動作チェックすること．

• void clear_array(double x[], int n); // 要素数 n の配列 x に，すべて 0 を代入する（初期化）．
  
• void square_wave(double x[], int n); // 要素数 n の配列 x に，任意の周波数（例えば 5 ）の矩形波を書き込む．振幅は任意，例えば -1 から 1 など．
  
  
• void sin_waves(double x[], int n, double f1, double f2, double f3);
  
  配列に周波数 f1, f2, f3，計3個の正弦波または余弦波の和を入れる．
  
  f > 1 とする． 例えば，
  

  
  #include <math.h>
  
  const double pi = 2.0*asin(1.0);
  
  for(i=0; i<n; i++) {
      x[i] = (  2.0  * sin(  2*pi*i/n * f1 )
              + 0.5  * cos(  2*pi*i/n * f2 )
              + 0.25 * sin(  2*pi*i/n * f3 );
  }
  

  など． sin,cos関数の係数の 2.0, 0.5, 0.25は振幅を適当に設定しただけなので，各自変更してよい． 可能であれば位相も変化させてみよ．
  
  

  square_wave関数，矩形波	sin_waves関数，正弦波の和
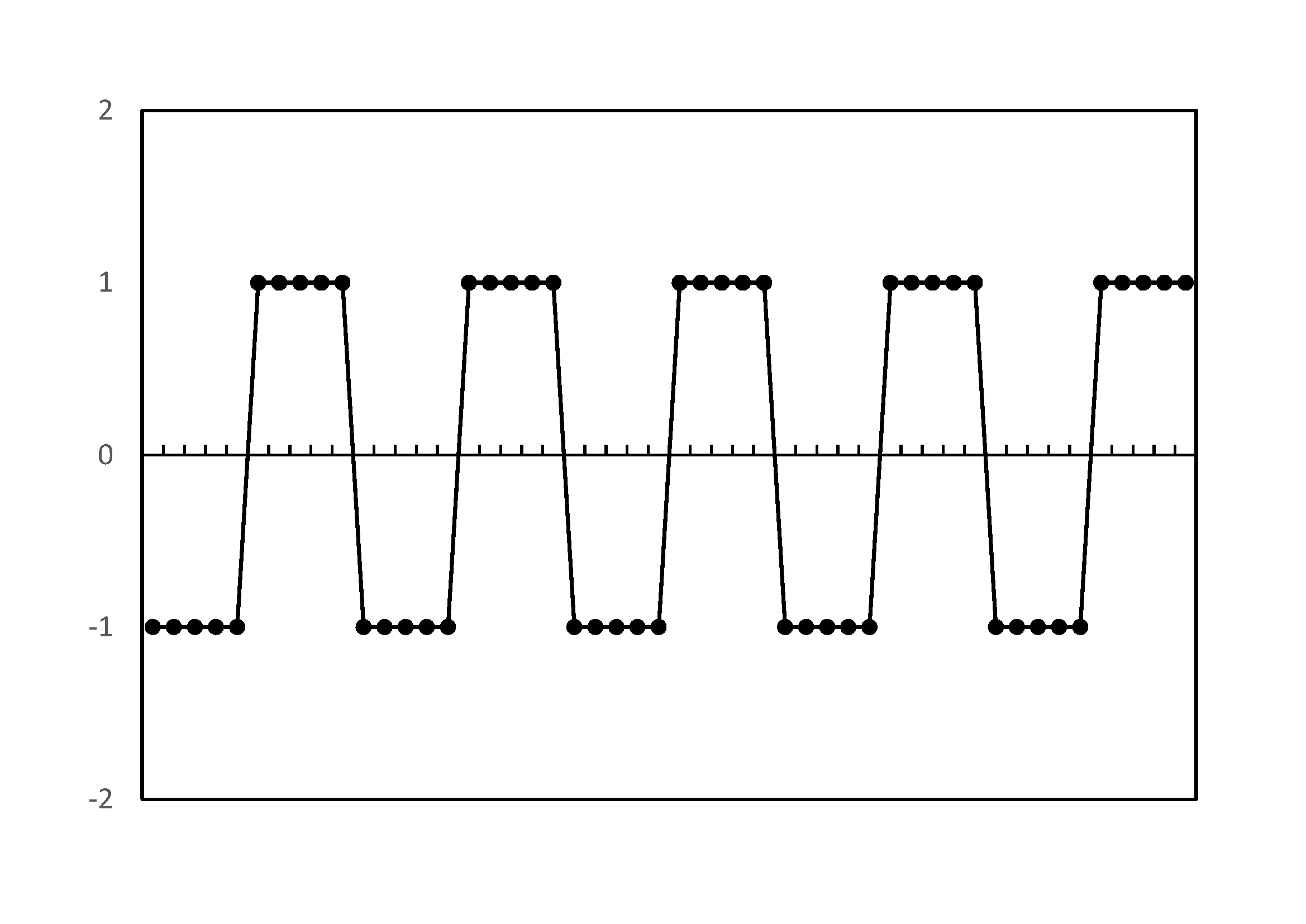  n=50, 周波数 5 の矩形波の例	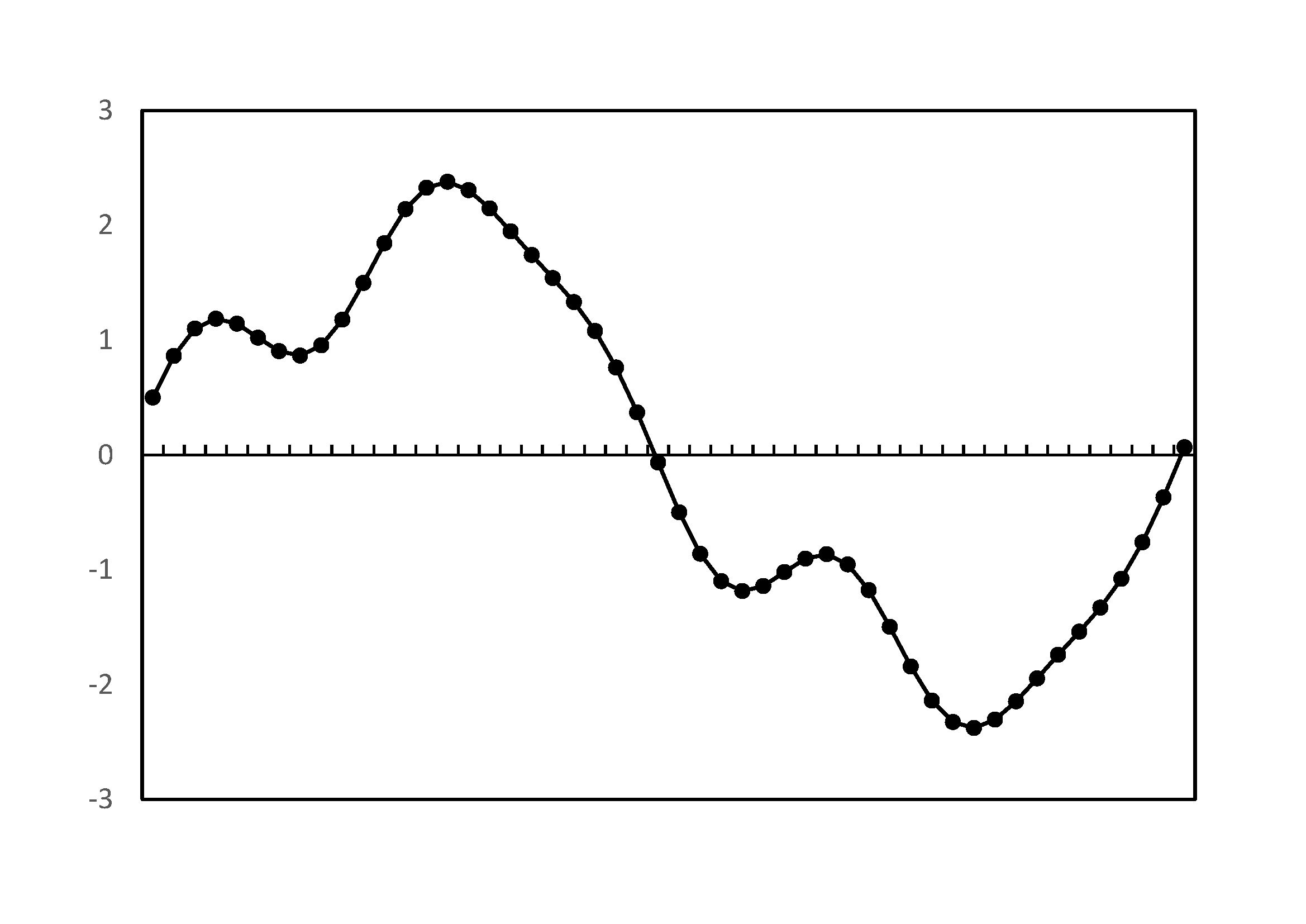正弦波，余弦波の和の例

課題2

離散フーリエ変換(DFT)と高速フーリエ変換(FFT)アルゴリズムについて文献等を調査し，簡単に説明せよ．
用いた文献名を明記すること．
テキストファイル(.txt)またはWordファイル(.docx)にて提出．
ファイル名は153R000000-07-2.txt または 153R000000-07-2.docx とする．

（発展的）課題3（できれば）

課題1で生成した波形データにたいして，本ページ内の離散フーリエ変換の式(2)，及び先週までに作成した複素数計算関数を用いて，F[0], F[2π], F[4π], ...などの値を計算してみよ．
計算結果はテキストファイル 153R000000-07-3.txt に貼り付けて提出せよ．