第3回　補間とスプライン(2)

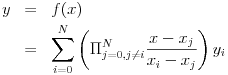
今回は，本格的な補完手法について実習を行う．

ラグランジュ補間（多項式による補間）

前回の課題では，2点から1次関数を決定したが，実用的には2次，3次関数など，高次の多項式による補間を行う場合も多い．

一般に，N+1個のデータからは N次式が決定でき，その際に必要な係数はN+1個となる．

独立したN+1個の座標値 (x₀, y₀), (x₁, y₁), (x₂, y₂), ... , (x_N, y_N) が与えられた場合に，これらの全ての点を通る関数を求める．
x_iは，全て異なるとする．

y = a₀ + a₁ x + a₂ x² + ... + a_N x^N 　　　　　(1)

係数 a_i をすべて求めれば関数が決まる．
関数が決まれば，既知である x_i 以外の，任意の x に対する y の値が得られる．
この係数は，N+1元の連立1次方程式を解くことにより求めることができる．

例：N = 2の場合

3個の既知の点群 (x₀, y₀), (x₁, y₁), (x₂, y₂)を，式(1)に代入することにより，以下の3本の方程式が得られる．

y₀ = a₀ + a₁ x₀ + a₂ x₀²
y₁ = a₀ + a₁ x₁ + a₂ x₁²
y₂ = a₀ + a₁ x₂ + a₂ x₂²

記号が多くあるが，x_i, y_i (i = 0,1,2) は既知の値なので，ここでは未知の係数a₀, a₁, a₂ を求める問題となる．
未知数が3個で，（独立な）方程式が3個あるので，係数aが一意に決まる．
しかし，補間に用いる点の個数が増えれば増えるほど方程式の数が増えるため，これらをまともに解くのは手間がかかる．

ところが，連立方程式を解くことなく，このような点群から明示的な形で関数値を得る巧みな手法が考案されており，ラグランジュ補間はその1つである．

ラグランジュ補間法では，以下の式を用いて，N+1 個の値 (x_i, y_i ) を元に，任意の x に対するy = f(x) の値を計算することができる．

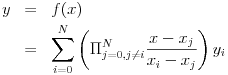
展開して書くと，以下の通りとなる．

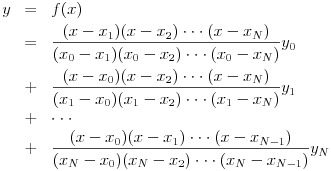
上の式を見ればわかる通り，既知の値を代入して計算するだけで，任意の x にたいする関数の値が計算できる．

本来であれば，上記の式をソースコードでどのように表すことができるかは，各自で考えて欲しいが，一例として以下にソースコードの参考例を示す．
実習課題作成にあたっては，少なくともこの関数がどのような処理をしているのかを充分に理解した後に使用すること．

関連するC言語キーワード：関数，配列，繰返し，条件分岐，構造体，四則演算


double LagrangeInterp(const Point2D pnt[], const int n, const double x)
/*
 * pnt   : 点群を表す配列
 * n     : 点群の個数
 * x     : 求めたいxの値
 * 戻り値 : xに対応する関数値 y
 */
{
    int i,j;
    /* 計算用変数の初期化 */
    double p, s = 0.0;

    for (i = 0; i < n; i++) {

        p = pnt[i].y;   /* 積の計算 */

        for (j = 0; j < n; j++) {
            if (i != j) {
                p *= (x - pnt[j].x) / (pnt[i].x - pnt[j].x);
            }
        }
        s += p;
    }

    return s;
}

このように，式で見ると複雑に見えるが，プログラムにすると意外とシンプルである．

課題1

先週の課題1と同じ5点の点群データを用いて，ラグランジュ補間を行ってみよう．
（n+1 点の点群から n次関数が決定できる．ここでは5点があるので，4次関数を決定する．）

上記の関数および下記を参考に，x の値を -4.0 から 3.0 まで，0.1 ずつ増加させてそれぞれ y を計算し，グラフを書け．
下記を参考に，ソースコードおよびExcelファイルを提出せよ．


struct Point2D
{
    double x;
    double y;
};
	
int main()
{
    const int N = 5;
	Point2D points[N] = {
        {-3.5, -2.2},
        {-2.2, -0.3},
        {-1.0,  1.5},
        { 0.2,  1.9},
        { 2.3,  2.2}
    };
	
    /* xの値を変化させながら LagrangeInterp 関数により y の値を順次計算，出力 */
}

以下に計算結果の一例を示す．

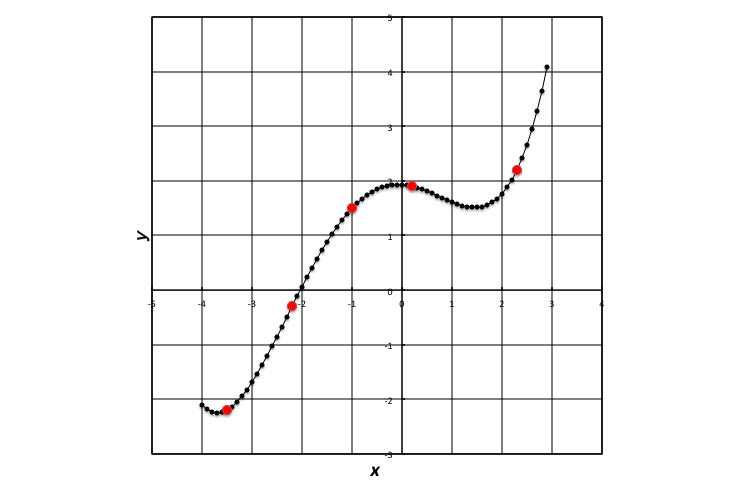
図1．補間結果．赤点が既知の制御点，黒丸が補間により求めた点群である．
Excelの機能で，補間により求めた点を線で接続している．

Excelでのグラフ作成法

参考までに，以下の手順でグラフを作成すると良い．
詳しくは各自でExcelのオンラインヘルプを参照のこと．

(x,y) の数値データをプログラムからcsv形式でファイルに書き出す．
A列にxの値，B列にyの値が格納されているとする．A,B列を選択状態にして，グラフで，散布図を作成する．
制御点を表示したければ，制御点に相当する行のC列にB列の値を5箇所，コピーした上で，A,B,C列を選択して同様に散布図を書く．マーカーの色や大きさを適宜調整して，計算結果と，与えた制御点を区別し，見やすいグラフにする．
もちろん工学グラフにふさわしい体裁に変更すること．（Excelの標準の書式のままでは ×）

スプライン補間

前章のラグランジュ補間では，データによっては意図しない形状になることがある．（4次関数なので，関数の両端が上昇か下降かのどちらかにしかならない．）
例えば，周期関数や指数関数，正規分布など，必ずしも多項式での近似がふさわしくない場合がある．

そこで，与えられた点群すべてを使って関数を決定するのではなく，局所的な数点のみを使って局所の関数（曲線）を決定し，かつ，その曲線が全体として滑らかに接続されるような補間法が広く利用されている．
その代表例がスプライン補間である．

スプライン補間では，点群全体から単一の多項式を求めるのではなく，「各区間」を次数の比較的低い多項式で近似する．
多項式にはいろいろ考えられるが，ここでは以下の3次式を用いる「3次のスプライン補間」を行う．
（この補間に1次式を用いると，線形補間となる）

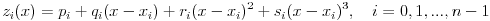
スプライン補間では，

与えられた点 (x_i, y_i) を全て，必ず通る
微係数の値が，各点ですべて一致する

ように，係数 p_i，q_i，r_i，s_i を決める．（一般に，両端の2乗の係数 r₀ = r_n-1 = 0 とする）．

課題2

スプライン補間の詳細なアルゴリズムは以下のソースコードおよび各種文献を参照すること．

153R000000?04?2.cpp

このソースコードを使用して，課題1と同様に5点の補間を行い，x の値を -4.0 から 3.0 まで，0.1 ずつ増加させてそれぞれ y を計算し，グラフを書け．
下記を参考に，ソースコードおよびExcelファイルを提出せよ．

また，ラグランジュ補間の結果と比較せよ．

以下に計算結果の一例を示す．

図2．補間結果，図1のラグランジ補間とスプライン補間の比較．赤点が既知の制御点である．
補間法により，通過する位置が大きく異なる区間がある．

発展的内容

以下は提出課題としては必須ではないが，補間法についてより深く勉強したい諸君のために，関連する課題を示しておく．

補間法において，制御点を追加すると曲線がどのように変化するだろうか．例えば(3,1)などを追加した場合，既存の関数形状がどう変化する．ラグランジュ補間とスプライン補間では，どのような差が生ずるか．
3次の補間が広く使われている理由はなんだろうか．
B?スプライン，ベジェ，エルミート補間など，他の補間法についても調べてみよう．

第3回 補間とスプライン(2)