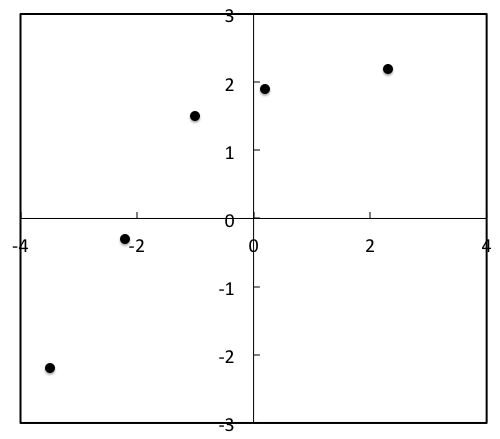
散布図の例
以下の手順に従ってソースフィルおよびグラフ等を作成せよ.
点群の座標値を画面に表示する関数disp_xy()を作成せよ.
テスト用main関数および実行結果を以下の通りとせよ.
struct Point2D
{
double x;
double y;
};
void disp_xy(const Point2D* pnt, const int n) /* この関数内で仮引数を変更しない場合はこのように書く.*/
{
...
}
int main()
{
const int N = 5;
Point2D points[N] =
{{-3.5, -2.2},
{-2.2, -0.3},
{-1.0, 1.5},
{ 0.2, 1.9},
{ 2.3, 2.2}};
disp_xy(points, N);
}
実行結果: -3.500000 , -2.200000 -2.200000 , -0.300000 -1.000000 , 1.500000 0.200000 , 1.900000 2.300000 , 2.200000
disp_xy()を改良して,点群の座標をcsvファイル 153Rxxxxxx-03-1.csv に出力(xxxxxxxは各自の学生番号)する関数fileout()を作成せよ.
引数および戻り値はdisp_xy()と同じで良い.
csvファイル内の各行に,カンマ区切りでx,yの座標値が格納されるようにすること.
前問で得られた csv ファイルをExcelで開いて.xlsx形式で保存し,散布図としてグラフを書け.
完成した.xlsxファイルおよびソースファイルを提出せよ.

散布図の例
前問において,各区間(計4区間)について,2点を通る1次関数を,式(1)を用いて求めよ. 計算結果として,x0およびx1の係数(つまり「切片」と「傾き」)を画面に表示せよ. ソースファイルを提出すること.
可能であれば,計算結果が正しいかどうか,グラフ用紙上,またはExcelで検証すること.(得られた切片と傾きから直線を書き,直線上に2点が存在するかを確認.)
実行結果(数値は適当であり,正しくない)
| 切片 傾き
--------+------------------
区間1 | 5.234 0.234
区間2 | 2.300 1.113
区間3 | -1.233 3.224
区間4 | 2.344 1.11
上記課題では,2点から1次関数による補間を行ったが,実際には2次関数,3時間数などの高次の多項式による補間を行う場合も多い. 一般に,N+1個の座標値 (x0, y0), (x1, y1), (x2, y2), ... , (xN, yN) が与えられた場合に,これらの全ての点を通る関数を求める.
N+1 個の値から,N次関数を1つ決定することができる.
例えば,2個の点が決まれば1次関数(直線),3個の点からは2次関数(放物線)が1つ決まる.
一般に,N+1個のデータからは N次式が決定でき,その際に必要な係数はN+1個となる.
y
= a0
+ a1 x
+ a2 x2
+ ...
+ aN xN
(1)
係数 aiをすべて求めれば関数が決まり,関数が決まれば任意の x に対する yの値が得られる.
一般的にこの係数は,N+1元の連立1次方程式を解くことにより求めることができる.
連立方程式の解法には多くの計算時間を要するが,ここでは良い方法がある.
各自で調べてみよう.
前述のラグランジュ補間では,多項式で任意の関数を表すものであるが,いくつか問題がある.例えば,周期関数や指数関数,正規分布など,必ずしも多項式での近似がふさわしくない場合がある.(多項式では,xが正負の無限大でその絶対値が無限大になってしまうが,sin, cos などは有限である.)
そこで,与えられた点群すべてを使って関数を決定するのではなく,局所的な数点のみを使って局所の関数(曲線)を決定し,かつ,その曲線が全体として滑らかに接続されるような補間法が広く利用されている.
その代表例がスプライン補間である.
次週に向けて,各自で調査・予習しておくこと.