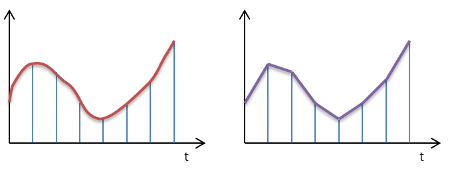
図1 台形則の原理.
左:まず関数を区間に分割 右:各区間を台形で近似
機械工学の分野では,剛体や連続体の運動が「微分方程式」で表される.
ところが,これらの微分方程式は,うまく解ける場合(解析解という)を除き,一般的には解析的を得ることは容易ではない.
例えば,以下は二次元の熱エネルギーの移動を表す「熱伝導方程式」と呼ばれ,2階の偏微分方程式である.
\begin{align*} \rho c \dfrac{\partial T}{\partial t} = k\left(\dfrac{\partial^2 T}{\partial x^2} + \dfrac{\partial^2 T}{\partial y^2} \right) + \dot{q} \end{align*}
$x,y$ は空間座標,$t$ は時刻,$T$ は温度,$\rho$
は密度,$k$ は熱伝導率,$c$ は比熱,$\dot{q}$
は内部発熱である.
この式を解くことによって,例えばスマートフォンや家電製品内の冷却,エンジンブロックの冷却,建物外壁の断熱などの解析などができる.
詳しくは熱力学,伝熱工学で学ぶ.
また,熱の移動のほかにも,流体力学では流体の挙動,電気工学では電磁波・光波の進行,機械力学では運動解析,材料力学では構造物の強度計算,などなど,工学では多くの微分方程式が扱われる.
この熱伝導(物体中を伝わる熱や温度分布)以外にも,電磁波・光波(アンテナの設計やレンズの設計),運動解析,構造物の強度予測,耐震設計,量子力学などなど,工学の応用分野においては,解析解が得られなくとも,ある一定の精度で数値解が得られれば良い場合が多い. そこで,計算機を用いた微分方程式の解法=数値解法が重要となる.
上記のような方程式系において,微分方程式を数値的に解くということは, その方程式を満足する変数(温度や圧力,速度)の値の時間変化を求めることにほかならず, その解は方程式を時間軸方向に積分することにより得られる.
積分は,計算機上では四則演算の繰り返しで近似的に表すことができる.
関数の近似方には様々なやり方がある.
例えば「台形則」では,下図の通り,対象とする関数の曲線をある区間ごとに短冊状に区切り, 区切られた点を結んだ直線による台形の面積を足し合わせていく.

図1 台形則の原理.
左:まず関数を区間に分割 右:各区間を台形で近似
台形則では,区切りが粗いと直線と曲線の軌跡の違いが大きくなるが,区切りを充分に細かくすれば,
それぞれの台形の面積は元の関数形に近づくと考えられる.
ところが,計算機では非常に多くの小さな値の乗算・加算を繰り返すと,計算による誤差(丸め誤差・打切り誤差)が累積するという問題がある.
そこで,こうした計算に起因する誤差を減らすために,数値積分には様々なアルゴリズムが存在する.
まず,最も単純な Eular 法(オイラー法)を試そう.
いま,時間を $t$ とし,関数 $f(t)$ は微分可能で,その導関数
$f'(t)$ が存在するとする.
微分方程式を差分にすると以下のように「近似」できる.
導関数は微小区間 $\Delta t$ の勾配を表すので,この微小区間を充分小さくとれば,誤差は減少する=真値に近づくと考えられる.
$\Delta t \rightarrow 0$ とすれば,微分の定義となる. これを変形して.
\begin{align*} f(t+\Delta t)=f(t)+\Delta t \times f'(t) \end{align*}
とする.
これをよく見ると,時刻 $t$ から微小時間 $\Delta
t$ 経過後の関数の値 $f(t+\Delta t)$ は,
$f(t)$ にたいして $\Delta t$ に傾き $f'(t)$
をかけたものを足して(近似的に)求まることを表している.
これがオイラー法の基本的な考え方である.
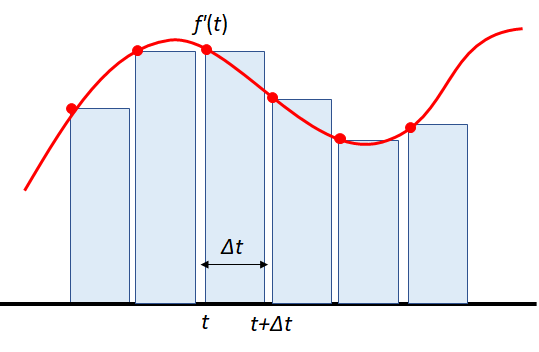
図2 Eular法.
また,時刻 $t=0$ での値 $f(0)$ (これを「初期値」という)と, 任意の時刻 $t$ での導関数 $f'(t)$ が判っているとして, この足し算を次々に繰り返し,関数の値を次々に計算してゆけば良い.
アルゴリズムは大変シンプルである.
計算に必要な値は,初期値,導関数の値 $f'(t)$
と,時間刻み幅 $\Delta t$
(時間ステップと言う)である.
シミュレーションにあたっては,$t=0$ から何秒まで行うのか,刻み幅はどのくらいにするのかを適切に決めて計算する.
以下の微分方程式の数値解をオイラー法による数値積分で求め,グラフに表せ. その際,解析解と比較せよ.
ヒント1:まず,(数学の)導関数を表す(C言語の)関数を定義せよ.
計算に必要な変数 $t, y$ などの値を渡すと,導関数の値
$f(t)$ を返す関数である.
double f_prime(double t, double y) /* 関数によっては t, y を使用しない場合もある. */
{
...
return ???;
}
ヒント2:時間刻み幅を 0.1, 0.01, 0.001 などと変化させ,解がどのように変化するか比較せよ.
答え合わせ用の解析解は,それぞれ各自で算出せよ.