フーリエ変換(1)
目次
はじめに
本日から,情報処理応用の一つとして「信号処理」を扱う.
信号処理とは,実験などで得られた何らかの波形データを(数学に基づいた)方法で加工し,その特徴を抽出したり,雑音を軽減したり,必要な情報を抽出したりする手法の総称である.
広い意味では,2次元データである画像などの解析(画像処理と呼ばれ,顔認識やモザイク処理,色調変換や画像圧縮など)も信号処理と呼ばれるが,ここでは簡単に1次元データの処理を考えよう.
ある信号波形データがあったとして,この波形から何か情報を抽出したいとする.
たとえば,音声信号から内容を推定したり,楽器や自動車の振動波形からその減衰特性や共振特性を把握したり,各種気象データから長期の気候変動を知りたい場合などがこれにあたる.
実際にはこれらの波形は単純な正弦波などには程遠く,複雑な信号波形であるため,いくら波形を眺めていてもよく分からない.
そこで,信号にどのような周波数(振動数※)成分が,どのくらいの大きさ(振幅,またはパワー)で含まれているかを解析することによって,その性質を把握することが出来る.
※周波数と振動数
どちらも単位はHzで似たようなものと考えられそうだが,以下のように区別される.
周波数は,電波,磁界,音などの信号を対象とした表現に用いられる.
また,「共振周波数」などの言葉の通り,積極的に発振させる意図を持った利用がなされる.
振動数は,機械の構造物や機構の応答に用いられる表現で利用される.
また,原子や分子の運動に関しても振動数が用いられる.
「固有振動数」という言葉の通り,対象とする物理系の持つ特性を考える場合に用いられる. |
複素数クラスの使い方
今回は複素数の扱いを通して,データ構造とアルゴリズムを組み合わせ,計算処理を進める基本を学ぶ.
また,フーリエ変換に対する準備でもあるので,しっかりと理解しよう.
C++の標準テンプレートライブラリ(STL)には,複素数を表すクラスcomplexが用意されている.
複素数クラスの宣言には,実部・虚部を表す変数の型を指定する必要があるが,ここでは
double 型を用いることとする.
また,関連する複素数の四則演算や絶対値,指数関数なども提供されている.
#include <complex> // これが必要
using namespace std;
int main(void)
{
complex<float> z1; /* float 型の複素数 */
complex<double> z2; /* double 型の複素数 */
};
参考:複素数の基礎的な演算
ここでは,複素数を $z=x+jy$ とする.
$x,y$ は実数である.$j$ は虚数単位で,$j^2=-1$
である.
数学では虚数単位として $i$ が使われるが,工学では電流$i$との混同を避けるため
$j$ が使われることも多い.
- [和]
- $z_1+z_2 = (x_1+jy_1) + (x_2+jy_2) = (x_1+x_2)
+ j(y_1+y_2)$
- [差]
- $z_1-z_2 = (x_1+jy_1) - (x_2+jy_2) = (x_1-x_2)
+ j(y_1-y_2)$
- [積]
- $z_1\cdot z_2= (x_1x_2-y_1y_2) + j(x_1y_2+x_2y_1)$
- [商]
- $z_1/z_2= (x_1x_2+y_1y_2)/(x_2x_2+y_2y_2)
+ j(x_2y_1-x_1y_2)/(x_2x_2+y_2y_2)
$
- [共役複素数(Conjugate)]
- $\overline{z}= x - j y$
- [絶対値]
- $|z|=(z\cdot\overline{z})^{1/2}=(x^2+y^2)^{1/2}$
- [ノルム]
- $\|z\|=z\cdot\overline{z}=x^2+y^2$
- [偏角]
- $\arg(z) = \tan^{-1}(y/x)$
- [指数関数]
- オイラーの式 $e^{j\theta}=\cos\theta+j\sin\theta$を用いて
$e^z= e^{x+jy}= e^x ( \cos y + j\sin y )$
- [累乗]
- 整数 $n$ に対して,
$z^n= r^n ( \cos n\theta + j\sin n\theta)$
ただし,$r = |z|$, $\theta = \arg(z)$
複素数型の使用例
#include <iostream> // これが必要
#include <complex> // これが必要
using namespace std;
int main(void)
{
complex<float> z; /* float 型の複素数 */
complex<double> z1, z2; /* double 型の複素数 */
/* 代入 */
z1 = complex<double> (0.2, 1.0); /* 0.2 + 1.0j を代入 */
z2 = complex<double> (1.8, -2.3); /* 1.8 - 2.3j を代入 */
/* 複素数を表示 */
cout << "z1 = " << z1 << endl;
cout << "z2 = " << z2 << endl;
/* 実部,虚部を別々に表示 */
cout << "Re{z1} = " << z1.real() << endl;
cout << "Im{z1} = " << z1.imag() << endl;
/* 四則演算 */
cout << "z1 + z2 = " << z1 + z2 << endl;
cout << "z1 - z2 = " << z1 - z2 << endl;
cout << "z1 * z2 = " << z1 * z2 << endl;
cout << "z1 / z2 = " << z1 / z2 << endl;
/* 共役複素数 */
cout << "conj(z1) = " << conj(z1) << endl;
/* 絶対値 */
cout << "abs(z1) = " << abs(z1) << endl;
/* ノルム */
cout << "norm(z1) = " << norm(z1) << endl;
/* 偏角 */
cout << "arg(z1) = " << arg(z1) << endl;
/* 指数関数 */
cout << "exp(z1) = " << exp(z1) << endl;
/* 累乗 */
int n = 10;
cout << "pow(z1, " << n << ") = " << pow(z1, n) << endl;
}
練習問題
- 上記のプログラムをコンパイルして,実行結果を確認せよ.
- 変数
z1, z2 の値を変更して,計算結果が変化すること,および,正しいことを確認せよ.
参考:複素数の宣言は文字数が多くなる傾向があるので,以下のように
typedef を用いて型名に別名を設定すると,少し簡単になる.
typedef complex<double> dcmpx;
int main()
{
dcmpx z1, z2; /* 複素数型変数の宣言 */
...
}
練習問題
純虚数 $z = 0 \sim 2\pi j$ までの区間を等分割(例えば100分割)し,
その区間の指数関数 $y = \exp(z)$を求めたい.
算術ライブラリのexp 関数を利用し,実部,虚部をカンマ区切りでファイルに出力(csvファイル)して,
- 複素数の実部,虚部を以下のように画面に表示せよ.(実部は
cos 関数,虚部は sin 関数となるはずである.)
- データをファイルに出力し,得られた $x,y$
の値を,複素平面状に散布図として描け
今後のために,複素数型の配列を使用する練習をしてみよう.
// 複素数型の配列の宣言と使用例
#include <iostream>
#include <complex>
#include <stdio.h>
using namespace std;
int main()
{
const int N = 100;
complex<double> z[N]; // 複素数型の配列
z[0] = complex<double> (1.0, 2.0); // 配列の先頭に,1+2i を代入
printf("re=%f, im=%f\n", z[0].real(), z[0].imag()); // 表示
return 0;
}
実行例
実部 , 虚部
1.000000, 0.000000
0.998027, 0.062791
0.992115, 0.125333
...
0.992115, -0.125333
0.998027, -0.062791
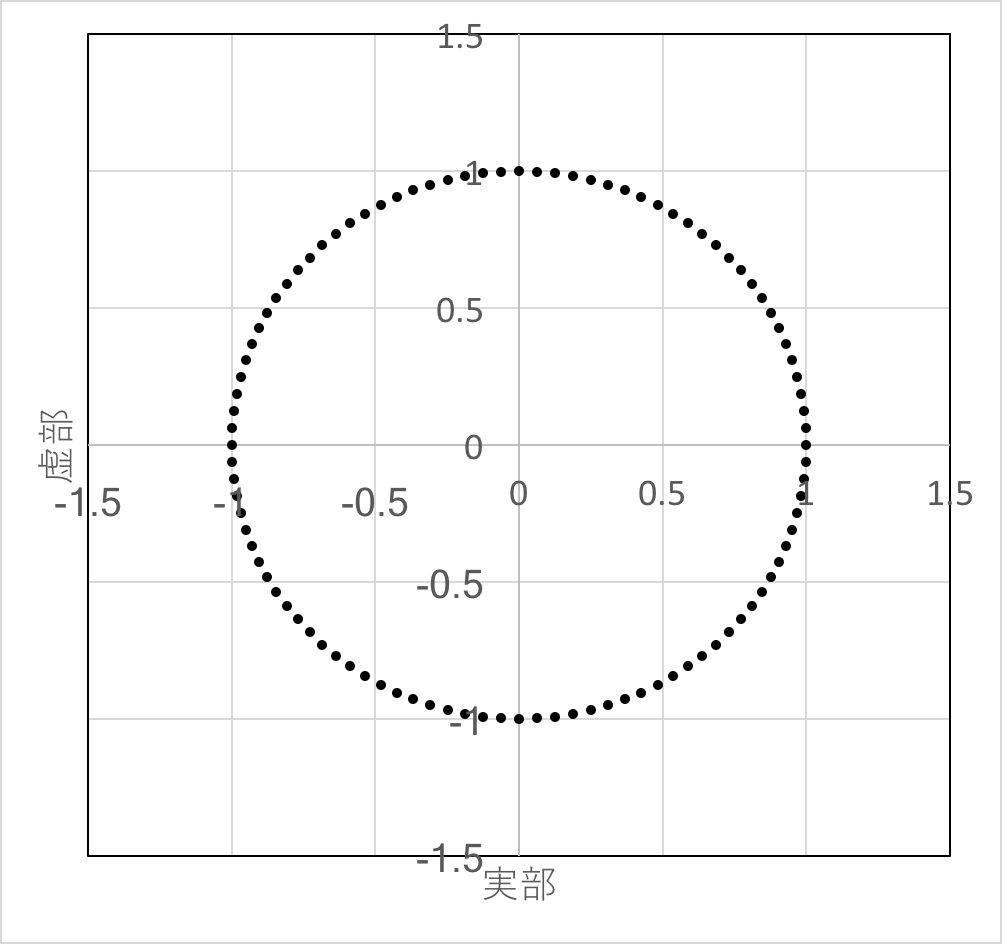
複素平面上での例.
純虚数の指数関数は,複素平面上で円を描く.
サンプリングについて
もともと連続的な信号を計測により一定の時間間隔で取得し,離散的なデータ列に変換することを「サンプリング,標本化」と言う.
測定する量の変化の速度よりも速く,即ち,十分短い時間刻みで値を連続的に計測する必要がある.
測定の時間刻みのことをサンプリング間隔と呼び,単位は時間(sec,
min等)となる.
たとえば,「一日の気温の変化」をサンプリングするには
1 時間おきの計測で十分だが,「エアコンの出力制御」では1分など短い時間間隔で温度をサンプリングする必要がある.
サンプリング間隔の逆数を「サンプリング周波数」と呼び,単位は
Hz である.
計測データは,一定のサンプリング時間の間隔で,配列に格納されていく.
時間軸上のデータは基本的に一次元配列データであるが,画像データなどは2次元配列データとなる.
サンプリングする時間間隔を $\Delta t$ とすれば,データ配列の
0 番目には $f(0)$,1番目には $f(\Delta t)$,2番目には
$f(2\Delta t)$・・・,といった計測データが順次入る.
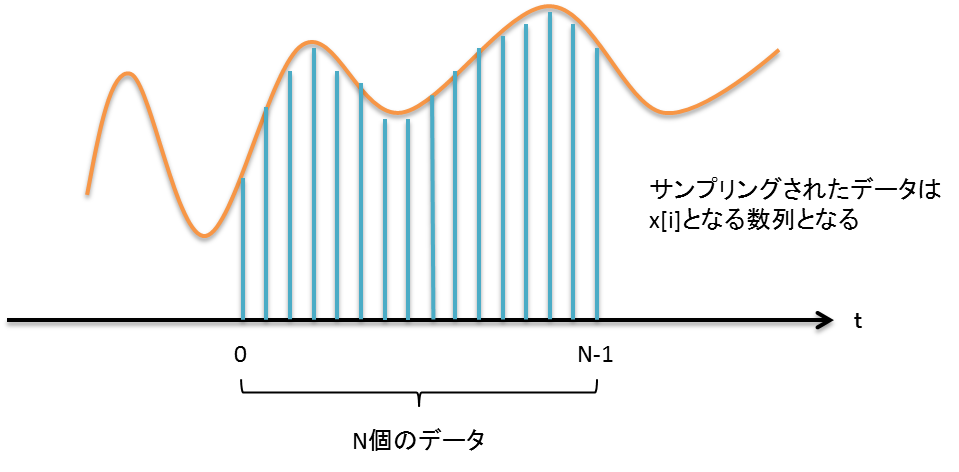
連続データのサンプリング(離散化とも言う).
フーリエ変換とは
(連続)フーリエ変換
まず,フーリエ変換(Fourier Transform)がどのような変換で,どのような性質かを理解しよう.
フーリエ変換とは,任意の関数を,様々な周波数の三角関数の和で表すものである.
フランスの数学者 Joseph Fourier により,固体の熱伝導方程式を解析するために提案された方法である.
時間 t に対して,連続な関数 f (t) に対して,フーリエ変換
F は以下のように定義される.
\begin{align}
F(\omega)=\int_{-\infty}^\infty f(t)\ e^{-j\omega
t}\ dt
\end{align}
$\omega$ は角周波数である.
(注:複素数の指数関数は周期関数でしたね.)
離散フーリエ変換
計測器などでコンピュータに信号を取り組んだ場合,必ず離散的,かつ,有限区間のデータの集合となり,具体的には配列に格納される.(無限長のデータは保存できない)
連続フーリエ変換の式は,連続な関数 $f$ に対して定義されるので,
これをサンプリングされた $N$ 個の離散データに対して適用すると,以下のようになる.
(ここでは,元データをC言語の配列風に f[t]
とする.)
\begin{align}
F[\omega]=\sum_{t=0}^{N-1} f[t]\ e^{-j\omega
\frac{t}{N}}\ dt
\end{align}
と表される.
$F[\omega]$が,フーリエ変換後の関数である.
これが離散フーリエ変換の基本形である.
右辺の指数関数の部分は,$\omega=2\pi,4\pi,6\pi$
と増加するにつれ,周波数が増加する.
即ち,離散フーリエ変換は,いろいろな周波数の余弦波・正弦波と,元の波形
$f$ との内積を計算することと等価である.
このように離散的なデータに対してのフーリエ変換を離散フーリエ変換(Discrete
Fourier Transform, DFT)と呼び,コンピュータで計算できるのはこのDFTである.
ところが,DFTはデータ数が大きくなると著しく計算負荷が高く(計算時間が
$N^2$ に比例)なるため,小さなデータ数しか計算できない問題があった.
1965年,James CooleyとJohn Tukeyにより,DFTの計算を劇的に高速化するアルゴリズムが開発された.
これが高速フーリエ変換(Fast Fourier Transform,
FFT)である.
高速フーリエ変換は,データ数 $N$ が小さな素数の積(最も良いのは2の累乗)の場合,$N$
が大きくなっても計算時間がさほど増加せず($N\log
N$ に比例),画像データなどの巨大なデータも一瞬で変換できるため,実用性が高まった.
フーリエ変換では,変換結果は一般的に複素数になる.
変換した関数の絶対値の2乗(=パワー)を縦軸に,横軸に周波数(または振動数)をとりグラフに表したものを,「パワースペクトル」と言う.
また,縦軸を振幅(の絶対値)としたものを,「振幅スペクトル」と呼び,いずれも周波数解析の重要な方法となっている.
以下に,パワースペクトル例を示す.
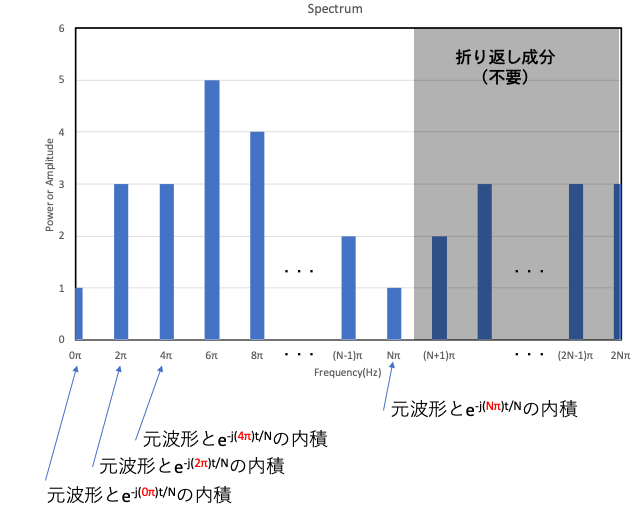
スペクトルの一例.横軸が周波数,縦軸が振幅(またはその二乗であるパワー)を表す.
どの周波数の振動が,どのくらいの割合で含まれるかを表している.


