コンピュータは,有限個のデータ(離散データという)であれば,メモリ容量の許す限り処理することができるが,
値が無限に必要な連続関数を「数値データ」として扱うことはできない.
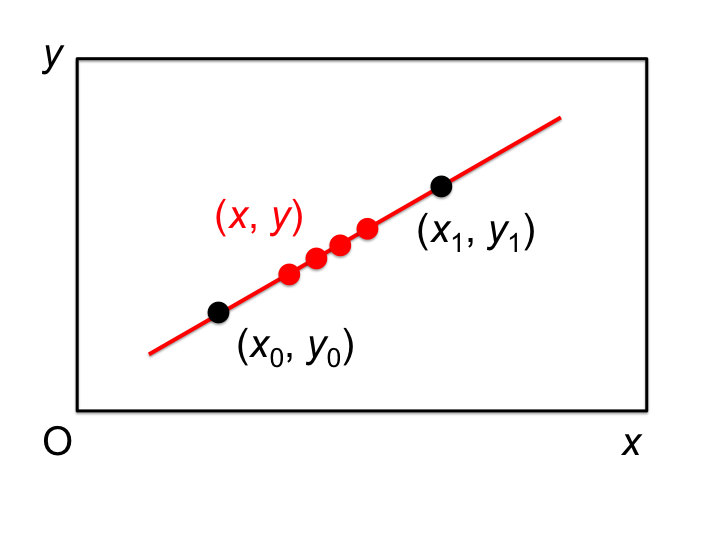
そこで,有限個の離散データをもとに,まずその点を必ず通る関数を決定し,それを用いてデータとして持っていない任意の関数値を得る方法を補間と呼ぶ.
一般に,関数の種類と,その係数を決定すれば,
その関数の任意の値(=任意の $x$ に対する
$y=f(x)$ の値)を計算することができる.
例えば,
などである.
補間には多くの種類があるが,ここで学ぶ基本的な手法を以下に示す.
もっとも単純な補間法は線形補間である.
線形補間では,2点から関数を決定することができるため,その区間内外の任意の点に対する関数値を決定することができる.

任意の2点に対する線形補間の式は以下のように表される. \begin{align} y - y_0 = \dfrac{(y_1-y_0)}{(x_1-x_0)} (x-x_0) 但し,x_0\neq x_1 \end{align}
これを用いて,任意の$x$にたいする$y$を計算することができる.
より高次の関数についても,多項式の各係数を決めることにより関数が決定できる.
点群から補間により関数を決定すれば,任意の場所の関数値を計算できるが,どの位置の値を得るかにより内挿と外挿とに分けられる.
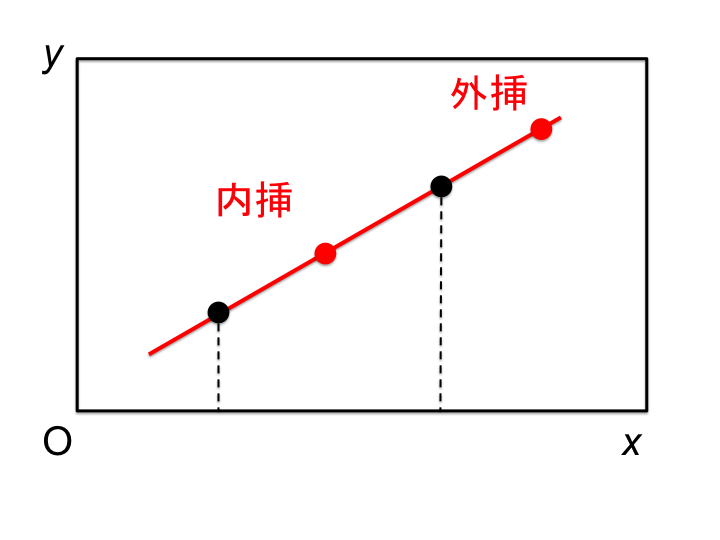
内挿 (interpolation)
外挿 (extrapolation)
一般的に内挿に比べて外挿はその値の信頼性について担保することが難しいことが知られている.
線形補間では,2点から1次関数を決定したが,実用的には2次,3次関数など,高次の多項式による補間を行う場合も多い.
独立した $N+1$ 個の座標値
$(x_0, y_0),
(x_1, y_1),
(x_2, y_2),
... ,
(x_N, y_N)$
が与えられた場合,1つの $N$ 次式が決定できる.即ちこれらの点群の全ての点を通る関数を求める.
$x_i$は,全て異なるとする.
$y= a_0+ a_1 x+ a_2 x^2+ ...+ a_N x^N$
この係数 $a_i$ をすべて決めれば,関数が一意に決まる.
関数が決まれば,既知である $x_i$ 以外のあらゆる
$x$ に対する $y$ の値が得られる.
この係数は,$N+1$ 元の連立1次方程式を解くことにより求めることができる.
3個の既知の点群 ($x_0, y_0$), ($x_1, y_1$), ($x_2, y_2$)を上式に代入することにより,以下の3本の方程式が得られる.
\begin{align*} y_0 = a_0 + a_1 x_0 + a_2 x_0^2 \\ y_1 = a_0 + a_1 x_1 + a_2 x_1^2 \\ y_2 = a_0 + a_1 x_2 + a_2 x_2^2 \end{align*}記号が多くあるが,$x_i, y_i$, $(i= 0,1,2)$
は既知の点群の座標値なので,ここでは未知の係数
$a_0, a_1,a_2$ を求める問題となる.
未知数が3個で,(独立な)方程式が3個あるので,係数
$a_i$ が一意に決まる.
補間に用いる点群の個数が増えるほど方程式の数が増えるため,これらをまともに解くのは手間がかかる.
ところが,連立方程式を解くことなく,このような点群から明示的な形で関数値を得る巧みな手法が考案されており,ラグランジュ補間はその1つである.
ラグランジュ補間法では,以下の式を用いて,$N+1$ 個の値 ($x_i y_i$) を元に,任意の $x$ に対する $y=f(x)$ の値を計算することができる.
\begin{align*} y&=f(x) \\ &= \sum_{i=0}^N \left( \Pi_{j=0, j\neq i}^{N}\dfrac{x-x_j}{x_i-x_j}\right) y_i \end{align*}展開して書くと,以下の通りとなる.
\begin{align*} y &= f(x) \\ &= \frac{(x-x_1)(x-x_2)\cdot\cdot\cdot(x-x_N)}{(x_0-x_1)(x_0-x_2)\cdot\cdot\cdot(x_0-x_N)} y_0 \\ &+ \frac{(x-x_0)(x-x_2)\cdot\cdot\cdot(x-x_N)}{(x_1-x_0)(x_1-x_2)\cdot\cdot\cdot(x_1-x_N)} y_1 \\ &+ \cdot\cdot\cdot \\ &+ \frac{(x-x_0)(x-x_1)\cdot\cdot\cdot(x-x_{N-1})}{(x_N-x_0)(x_N-x_2)\cdot\cdot\cdot(x_{N}-x_{N-1})} y_N \\ \end{align*}
上の式を見ればわかる通り,既知の値を代入して計算するだけで,任意の $x$ にたいする値 $y$ が四則演算だけで計算できる.
本来であれば,上記の式をもとに,Cソースコードを各自で考えて欲しいが,一例として以下にソースコード例を示す.
実習課題にあたっては,これらの関数がどのような処理をしているのかを充分に理解した後に,各自でプログラムを組み立てて使用すること.
(Copy & Pasteでの使用は不可)
関連するC言語キーワード:関数,配列,繰返し,条件分岐,構造体,四則演算
struct Point2D // 点の座標を表す構造体
{
double x;
double y;
};
double LagrangeInterp(const Point2D pnt[], const int n, const double x)
/*
* pnt : 点群を表す配列
* n : 点群の個数
* x : 求めたい x の値(点群以外の任意の値でもOK)
* 戻り値 : xに対応する関数値 y
*/
{
int i,j;
/* 計算用変数の初期化 */
double p, s = 0.0;
for (i = 0; i < n; i++) {
p = pnt[i].y; /* 積の計算 */
for (j = 0; j < n; j++) {
if (i != j) {
p *= (x - pnt[j].x) / (pnt[i].x - pnt[j].x);
}
}
s += p;
}
return s;
}
このように,式で見ると複雑に見えるが,プログラムにすると意外とシンプルである.
前章のラグランジュ補間では,データによっては意図しない形状になることがある.
(4次関数なので,関数の両端が上昇か下降かのどちらかにしかならない.)
例えば,周期関数や指数関数,正規分布など,必ずしも多項式での近似がふさわしくない場合がある.
そこで,与えられた点群すべてを使って関数を決定するのではなく,局所的な数点のみを使って局所の関数(曲線)を決定し,かつ,その曲線が全体として滑らかに接続されるような補間法が広く利用されている.
その代表例がスプライン補間である.
スプライン補間では,点群全体から単一の多項式を求めるのではなく,「各区間」を次数の比較的低い多項式で近似する.
多項式にはいろいろ考えられるが,ここでは以下の3次式を用いる「3次のスプライン補間,cubic
spline」を行う.
(補間に1次式を用いると,線形補間=折れ線近似となる)
\begin{align*} z_i(x) = p_i + q_i(x - x_i) + r_i(x - x_i)^2 + s_i(x - x_i)^3, \ \ \ i = 0,1, ... , n-1 \end{align*}
スプライン補間では,
ように,係数 $p_i,q_i,r_i,s_i$ を決める. (一般に,両端の2乗の係数は $r_0 = r_{n-1} = 0$ とする).
以下の手順に従って,計算データを出力する方法を理解したうえで,グラフ等を作成せよ.
注:使用中のPCやMacに,Microsoft Excelがインストールされていない場合は,無償の各種Office互換ソフト(Apache OpenOffice,LibreOfficeなど)や,Numbers などを用いても良い. その場合は,提出時に .xls 形式,まかは .xlsx 形式にエクスポートして提出すればOK.
以下のような点群を表す構造体の配列に,座標値データが格納されている.
この座標値を画面に表示する関数 disp_xy() を作成せよ.
テスト用 main 関数,および実行結果を以下の通りとせよ.
C++のクラスにしてもよい.
class Point2D としたうえで,disp_xy() をそのメンバ関数にする.
struct Point2D
{
double x;
double y;
};
void disp_xy(const Point2D pnt[], const int n)
// nはデータ数.関数内で引数を変更しない場合は const としておくと良い.
{
...
}
int main()
{
const int N = 5;
Point2D points[N] = // データの例
{{-3.5, -2.2},
{-2.2, -0.3},
{-1.0, 1.5},
{ 0.2, 1.9},
{ 2.3, 2.2}};
disp_xy(points, N);
return 0;
}
実行結果: -3.500000 , -2.200000 -2.200000 , -0.300000 -1.000000 , 1.500000 0.200000 , 1.900000 2.300000 , 2.200000
次に,disp_xy()を改良して,点群の座標を画面ではなくファイルに出力せよ.
拡張子を .csv(カンマ区切りファイル)とする.
(csv ファイルはテキストファイルで,ファイル内の各行に,カンマ区切りで
x , y の座標値を格納する.)
.csvファイルの中身: -3.500000 , -2.200000 -2.200000 , -0.300000 -1.000000 , 1.500000 0.200000 , 1.900000 2.300000 , 2.200000
ファイル名を 153Rxxxxxx-04-1.csv とする.
前問で得られた csv ファイルを(ダブルクリックで)Excelで開き,まず,「名前を付けて保存」から,拡張子を.xlsx
形式と変更して保存せよ.
(この形式でないと,グラフが保存されない)
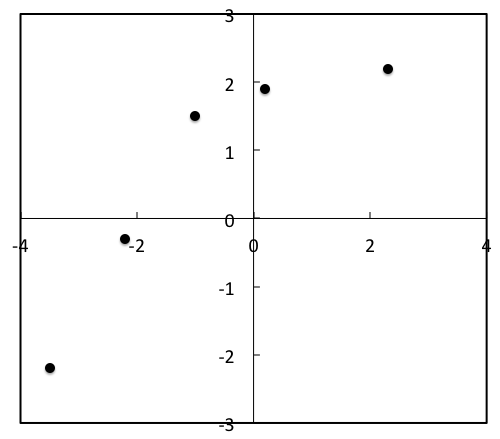
次に,下記のように「散布図」としてグラフを書け.
Excelの詳しい操作方法,グラフの書き方については,Excelのヘルプ,オンラインヘルプを参照すること.
Microsoft社製の表計算ソフト,Excelを用いてグラフを作成する場合は,以下の参考にすると良い.
詳しくは各自でExcelのオンラインヘルプを参照のこと.
商用のグラフ作成ソフトウエアとしては,IGOR,
DeltaGraph, SigmaPlot, Tecplot, などがある.
無料の科学技術用のグラフ描きソフトでは,ParaView,
Gnuplotなどが有名である.
これ以外にも非常に多くのソフトウエアがあるので,グラフの提出はExcelではなく専用のツールを用いて作成した図を提出しても良い.(但し,汎用性の高いjpg,png等の画像形式で提出すること.開けないファイルでは採点不可のため.)
Python言語では,matplotlibと呼ばれるパッケージ(拡張機能)が利用可能であり,簡単にグラフなどを表示できる.
グラフの元となる数値データと,数行のコードでExcelのグラフのような表示ができる.
この例では,matplotlibおよびnumpyパッケージを使用している.インストール方法はこちらを参照.
matplotlibのインストール方法(Mac)
アクセサリのターミナルから
$ sudo pip3 install matplotlib
password: (管理者のパスワードを入力)
Collecting matplotlib
Downloading matplotlib-3.3.2-cp38-cp38-macosx_10_9_x86_64.whl (8.5 MB)
|????????????????????????????????| 8.5 MB 5.3 MB/s
matplotlibのインストール方法(Windows)
「コマンドプロンプト」を管理者として実行し,
> pip install matplotlib ...省略...
この際,他の関連パッケージもインストールされる場合がある.
簡単なグラフを書くプログラム
import numpy as np
import matplotlib.pyplot as plt
X = np.linspace(-5, 5, 100)
Y = X**2
plt.plot(X, Y)
plt.show()
Pythonで散布図を描くサンプルソースコード
import numpy as np
import matplotlib.pyplot as plt
X = [ 1.1, 2.05, 3.0, 4.1, 5.0, 5.9, 7.1, 7.8, 8.9, 10.0]
Y = [ 1.0, 2.1 , 2.9, 4.05, 5.01, 5.99, 7.0, 8.1, 8.7, 9.5 ]
# 散布図を描く
plt.scatter(X, Y)
# タイトル,軸ラベル,グリッドの設定
plt.title('relation between force and strain.')
plt.xlabel('x (kg)')
plt.ylabel('y (m)')
plt.grid(True)
# 画面に表示
plt.show()